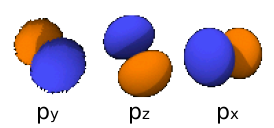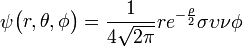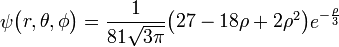Η Ιστορία των Φυσικών Επιστημών. Μέρος Έβδομο: Πέρα από την Κλασσική Φυσική ΙΙ. Η Κβάντωση των Φυσικών μεγεθών: Η Ερμηνεία των κβαντικών φαινομένων από "σκληρά" Μαθηματικά
της Δήμητρας Σπανού καθηγήτριας χημικού
για τον Μίμη και τους φίλους του
Κλείνω την ιστορία μου,
φορώντας δυο κόκκινα παπούτσια
Γιατί άλλο τι δεν έχω να πω.
Στην προσπάθεια να υπολογιστούν τα κβαντικά μεγέθητου μικρόκοσμου και δεδομένου πως στον κόσμο αυτόν, λαμβάνουμε υπ όψην την κυματοειδή μορφή των σωματιδίων, διατυπώθηκαν μαθηματικοί τρόποι, που αφ ενός κατοχύρωσαν και απέδειξαν την κβαντική θεωρία, αφ ετέρου μπόρεσαν με την επίλυσή τους να δώσουν μια εικόνα για το τι είναι και που βρίσκονται και κινούνται τα ηλεκτρόνια των ατόμων και των μορίων
William Hamilton
 Ιρλανδός φυσικός, αστρονόμος και μαθηματικός (1805-1865) Βραβείο Νόμπελ 1932
Ιρλανδός φυσικός, αστρονόμος και μαθηματικός (1805-1865) Βραβείο Νόμπελ 1932
εισάγει τελεστή για την μηχανική ενέργεια σωματιδίου
Τελεστής είναι κάθε απεικόνιση ενός συνόλου μαθηματικών αντικειμένων σε ένα άλλο σύνολο που συνήθως είναι ο εαυτός του
με την στήριξη της αναλυτικής μηχανικής του Ιρλανδού μαθηματικού William Hamilton , ο Schrodinger πέτυχε να διατυπώσει τις εξισώσεις του στην συνέχεια,
Ο Ηamilton, που με την δουλειά του συσχέτισε και έδωσε μαθηματικά μοντέλα, σε θέματα και μεγέθη της φυσικής μηχανικής, εδώ εισάγει έναν τελεστή που σχετίζεται με την μηχανική ενέργεια για ένα σωματίδιο (που κινείται σε μια διάσταση)
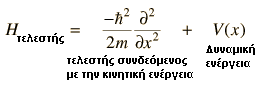 ο τελεστής του Hamilton
ο τελεστής του Hamilton
Αυτόν χρησιμοποιεί αργότερα ο Strondinger στην προσπάθειά του να περιγράψει την συμπεριφορά των ηλεκτρονίων ενός ατόμου όπου προφανώς με αυτόν τον τρόπο, καταφέρνει να εισάγει στις εξισώσεις του τον παράγοντα μηχανική ενέργεια ή να εισάγει στον τελεστή της μηχανικής ενέργειας την κυματική συμπεριφορά των σωματιδίων
Louis de Broglie Γάλλος Φυσικός ( 1892 - 1987)
 Κυματική θεωρία της ύλης 1924 Νόμπελ Φυσικής 1929
Κυματική θεωρία της ύλης 1924 Νόμπελ Φυσικής 1929
Το ηλεκτρόνιο παρουσιάζεται σαν σωματίδιο και σαν κύμα με 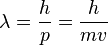 . Από την σχέση αυτή θα πρέπει το λ να παίρνει τιμές πολύ μεγαλύτερες από την διάμετρο των ατομικών πυρήμων ώστε να έχει νόημα η περιστροφή του γύρω από τον πυρήνα
. Από την σχέση αυτή θα πρέπει το λ να παίρνει τιμές πολύ μεγαλύτερες από την διάμετρο των ατομικών πυρήμων ώστε να έχει νόημα η περιστροφή του γύρω από τον πυρήνα
Erwin Schrödinger
 Αυστριακός φυσικός. ( 1887- 1961) Βραβείο Nobel μαζύ με Dirac το 1933
Αυστριακός φυσικός. ( 1887- 1961) Βραβείο Nobel μαζύ με Dirac το 1933
...το δικό του ανεξάρτητο δρόμο περιγράφοντας μαθηματικά το άτομο με τον ίδιο τρόπο που περιγράφουμε ένα σύστημα που ταλαντώνεται, και εισάγοντας αξιωματικά την ισοδυναμία όλων των δυνατών φυσικών ταλαντώσεων (ιδιοταλαντώσεων) αυτού του συστήματος με τις ευσταθείς ενεργειακές καταστάσεις του ατόμου....(.physics4u.gr)
Εισάγει τις Εξισώσεις Schrödinger το 1927 που η επίλυσή τους δίνει την πιθανότητα εύρεσης του ηλεκτρονίου ενός ατόμου, σε ορισμένο χώρο
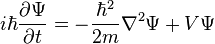
Στο πρώτο μέρος παίρνουμε την αλλαγές στο σχήμα της Ψ με τον χρόνο
Στο δεύτερο μέρος ο πρώτος όρος (Λαπλασιανή) δίνει την περιγραφή της μεταβολής στον χώρο και ο δεύτερος όρος περιγράφει τις δυνάμεις που δρουν στο σωματίδιο
Σε κάθε χρονική στιγμή η εξίσωση δίνει τιμή σε κάθε σημείο του χώρου
Σε κάθε σημείο του χώρου αποδίδονται στην κυματοσυνάρηση δύο αριθμοί
Οι εξισώσεις Schrodinger που βρίσκουν εφαρμογή σε σωματίδια των οποίων
α. ο αριθμός πρέπει να παραμένει σταθερός
β. Δεν πρέπει να κινούνται με πολύ υψηλές ταχύτητες
γ. Να είναι σωματίδια όχι φωτόνια
Συσχετίζουν την κυματική και σωματιδιακή συμπεριφορά και ανοίγουν τον δρόμο για την κβαντομηχανική
Με αυτές τις εξισώσεις, υπολογίζεται η Ενέργεια του ηλεκτρονίου ενός ατόμου, και η πιθανότητα εύρεσης του ηλεκτρονίου αυτού σε ορισμένο χώρο
Δεδομένου ότι το ηλεκτρόνιο εκτελεί περιοδικές κινήσεις, κινούμενο γύρω από τον πυρήνα, ή απο τους πυρήνες, εάν πρόκειται για μόριο, χρησιμοποιήθηκαν, το μαθηματικό μοντέλο του ταλαντωτή και οι εξισώσεις κύματος. Αυτή η κατάσταση περιγράφεται από την κυματοσυνάρτηση Ψ που παίρνει τιμές ανάλογα με την χρονική στιγμή και το σημείο που επιλέγουμε. Η συνάρτηση αυτή είναι μιγαδική και οι λύσεις μπορούν να δωθούν έτσι: ![]()
Η πιθανότητα να βρίσκεται ένα σωματίδιο σε χώρο ΔV και απόσταση r από τον πυρήνα έχει ερευνηθεί ήδη από τον Max Bohr
Για την πιθανότητα εύρεσης σωματιδίου σε στοιχειώδη όγκο ΔV σε συγκεκριμένο σημείο (x, ψ, z) , ο Bohr πρότεινε το γινόμενο του τετράγωνου της συνάρτησης επί το ΔV
Η συνολική πιθανότητα να βρεθεί το ηλεκτρόνιο σε ολόκληρο τον χώρο ευρίσκεται με την ολοκλήρωση της προηγούμενης σχέσης και ισούται με την μονάδα
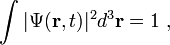
Εισάγωντας την κυματοσυνάρτηση Ψ στον τελεστή του Hamilton ο Erwin Schrodinger κανονικοποιεί την πρώτη και καταλήγει στην περίφημη εξίσωση
![]() Χρονικά ανεξάρτητη και Για μια διάσταση χ (αποτελεί γενίκευση της υπόθεσης DE Broglie
Χρονικά ανεξάρτητη και Για μια διάσταση χ (αποτελεί γενίκευση της υπόθεσης DE Broglie
Η αλλαγή από τη µια αναπαράσταση στην άλλη, δηλαδή η αλλαγή από ορισµένες ανεξάρτητες µεταβλητές σε άλλες, λέγεται κανονικός µετασχηµατισµός
Η λύση της εξίσωσης του Schrodinger είναι συχνά ένα πολύ δύσκολο πρόβληµα.
α. Σε µια κατηγορία προβληµάτων, η ενέργεια είναι σταθερή και οι ϕυσικές ιδιότητες δεν µεταβάλλονται µε το χρόνο Η εξίσωση καταλήγει σε 2ης τάξης
Το δυναµικό V (r, t) μέσα στον συντελεστή Hamilon δεν εξαρτάται από το χρόνο, δηλαδή V (r, t) = V (r). Δίνεται ένα σύνολο λύσεων που προκύπτουν από καθορισμένες τιμές ενέργειας και επίσης μπορούν να δώσουν πληροφορίες για το σύστημα που εξετάζεται
β. Στην άλλη περίπτωση η εξίσωση του Schrodinger είναι εξαρτηµένη από το χρόνο.
Επειδή η εξίσωση είναι μιγαδική δεν μπορούμε εύκολα να ανιστοιχίσουμε την φυσική της σημασία γιατί τα φυσικά μεγέθη αντιστοιχούν σε πραγματικούς αριθμούς. Έτσι χρειάζεται να βρούμε άλλα παράγωγα μεγέθη από αυτήν όπως είναι το τετράγωνο του µέτρου της, |Ψ(r, t)| 2 , που είναι πραγµατική συνάρτηση και εποµένως ϑα µπορούσε να δοθεί ϕυσική ερµηνεία σε αυτό.
Αυτή η φυσική ερμηνεία είναι η πυκνότητα της πιθανότητας να βρίσκεται το σωματίδιο τη χρονική στιγµή t στον όγκο dr = dxdydz στο σηµείο r
και είναι ανάλογη του |Ψ(r, t)| 2dr:
Σημείωση: Με βάση την εξίσωση αυτή του Erwin Schrödinger αλλά και την θεωρία της σχετικότητας ο Βρετανός θεωρητικός Φυσικός Paul Dirac θα καταλήξει το 1930 με την ομόνυμη εξίσωση, να επιβεβαιώση την ύπαρξη των αντισωματιδίων και της αντιύλης
Werner Heisenberg, (1901 - 1976)
 Θεμελίωσε την Κβαντομηχανική. Βραβείο Νόμπελ 1932
Θεμελίωσε την Κβαντομηχανική. Βραβείο Νόμπελ 1932
Διατύπωσε την αρχή της απροσδιοριστίας σε αντίθεση με την αρχή της αιτιοκρατίας το 1927
Εδώ διαλύονται και οι τελευταίες προσκολήσεις στην εικόνα που έχουμε, για έναν κόσμο σταθερό. υλικό και συγκεκριμένο. Το μικρότερο έως τότε από τα γνωστά υλικά σωματίδια δεν μπορεί να θεωρηθεί πια εντελώς υλικό και προσδιορίσιμο ούτε κατα το μέγεθος τη θέση και την ορμή, αφού κατά τον Heisenberg το μέγεθος τη θέση και την ορμή, τα αντικαθιστά η πιθανότητα να βρίσκονται σε μια θέση ή να έχουν μια τιμή για την ορμή κ.λ.π.
....Ο Heisenberg διατύπωσε λοιπόν, με βάση τα παρατηρούμενα μεγέθη και με τη βοήθεια των μητρών, το στρυφνό και έντονα μαθηματικοποιημένο πρώτο μοντέλο της Κβαντικής Μηχανικής....(.physics4u.gr).
Ο κυματοσωματοδυισμός της ύλης έχει πια αναγνωριστεί.

Robert Sanderson Mulliken, (1896 – 1986)
Αμερικανός φυσικός και χημικός
 Βραβείο Νόμπελ Χημείας 1966
Βραβείο Νόμπελ Χημείας 1966
Για τον χώρο εύρεσης των ηλεκτρονίων πρότεινε την λέξη “τροχιακό” 1932
ήταν ένας ο οποίος συνέβαλε αποφασιστικά στην ανάπτυξη της μοριακής φυσικής. Έλαβε το Βραβείο Νόμπελ Χημείας το 1966.
Τροχιακό: Η λύση της εξίσωσης Σρέντινγκερ δίνει ένα σύνολο κυματοσυναρτήσεων καθεμιά από τις οποίες αντιστοιχεί σε συγκεκριμένη τιμή ενέργειας του ηλεκτρονίου
Ατομικό τροχιακό: Όταν η επίλυση της εξίσωσης Schrödinger οδηγεί στις κυματοσυναρτήσεις ψ που περιγράφουν την κατάσταση του ηλεκτρονίου με ορισμένη ενέργεια (Εn)
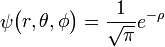 , όπου
, όπου  , με
, με  « ακτίνα Bohr ».
« ακτίνα Bohr ».
-
3px: n=3, =1:
=1: 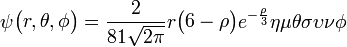 .
. -
3py: n=3,
 =1:
=1:  .
. -
3pz: n=3,
 =1:
=1: 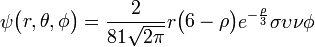
- Αυτά είναι λοιπόν τα ατομικά τροχιακά ή αλλιώς οι τροχαιές όπως τις συνέλαβε αρχικά ο Bohr που δεν είναι βέβαια κυκλικές όμως είναι κοντά στην ιδέα που είχαν τότε. Βέβαια εφ όσον τα τροχιακά προκύπτουν από πιο πολύπλοκες εξισώσεις, δεν έχουν το σχήμα που πρότειναν τότε το 1913, όμως η ιδέα τους ήταν γενικά σωστή ώστε τελειοποιήθηκε αργότερα
Γενικά
Αυτές οι κυματοσυναρτήσεις μέσω της κβαντικής θεωρίας προσδιορίζουν μια περιοχή του τρισδιάστατου χώρου στην οποία υπάρχει πιθανότητα να βρεθεί το ηλεκτρόνιο ενός ατόμου. Και κάθε ηλεκτρόνιο ενός ατόμου βρίσκεται σε ένα ορισμένο τροχιακό.
Αυτές οι μαθηματικές διατυπώσεις των κβαντικών φαινομένων από τον Hamilton , Heisenberg, Schrodinger , de Broglie , Mulliken, είχαν την συνέχειά τους
Με την επεξεργασία των εξισώσεών τους και των άλλων μαθηματικών σχέσεων, (όπως την τροποποίηση του τελεστή) πέτυχαν στην συνέχεια την διατύπωση νέων μαθηματικών σχέσεων, για τις οποίες έγινε δυνατή η αντιστοίχιση με τα άλλα φυσικά μεγέθη,
Έτσι μπόρεσαν να διατυπώσουν και να επεκταθούν και σε άλλα φυσικά φαινόμενα υπό το πρίσμα της νέας θεωρίας
Παραδείγματα
α. Κβαντική ορμή
Για ένα σωματίδιο χωρίς ηλεκτρικό φορτίο και χωρίς σπιν, ο τελεστής της ορμής μπορεί να γραφεί ως
όπου:
![]()
- β. Αβεβαιότητα χρόνου ενέργειας
-

- που έχει ένα εντελώς διαφορετικό φυσικό νόημα γιατί ο χρόνος δεν είναι απλά ένα φυσικό μέγεθος αλλά μια παράμετρος που συνοδεύει τις μετρήσεις
- γ. το ηλεκτρικό δυναμικό του ηλεκτρονίου που περιστρέφεται γυρω από έναν πυρήνα ή περισσότερους πυρήνες
- Χρειάστηκε να βάλουν διαφορετικούς τελεστές για να πάρουν τις σωστές τιμές για τα μεγέθη αυτά, όπως είναι τελεστής του Hamilton, που συσχετίζεται όπως αναφέρθηκε με την ενέργεια του συστήματος
-
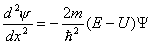
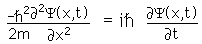
- Με αντίστοιχους τρόπους σχεδιάζονται και τα μοριακά τροχιακά
-
 τροχιακά στο μόριο του μεθάνιου CH4
τροχιακά στο μόριο του μεθάνιου CH4 - δ. ηλεκτρόνιο παγιδευμένο σε πηγάδι δυναμικού
-
 Εδώ η λύση της εξίσωσης Στροντιγκερ είναι
Εδώ η λύση της εξίσωσης Στροντιγκερ είναιΨ(x) = 0 αν x<0 ή x>L και
Ψ(x) = Αημ
 για 0≤ x ≤ L όπου n=1,2,3....
για 0≤ x ≤ L όπου n=1,2,3.... -
λ =
 (n=1,2,3....)
(n=1,2,3....)  το μήκος κύματος και η ορμή παίρνουν ορισμένες τιμές
το μήκος κύματος και η ορμή παίρνουν ορισμένες τιμές 
Οι πέντε θεμελιώδεις προτάσεις της κβαντομηχανικής
1. Μαθηματική περιγραφή των φυσικών καταστάσεων με μια κυματοσυνάρτηση τετραγωνικά ολοκληρώσιμη
2. Μαθηματική περιγραφή των φυσικών μεγεθών, σε κάθε ένα τους αντιστιχεί ένας τελεστής
3. Στατιστική ερμηνεία
4. Νόμος της κβαντικής μέτρησης όπου η κατάσταση ενός φυσικού συστήματος μετά από την μέτρηση δίνεται από την ιδιοσυνάρτηση που προκύπτει αν θέσουμε την ιδιοτιμή που μερήθηκε
5. Ο κβαντικός νόμος της κίνησης

Η κβάντωση στην δημιουργία χημικού δεσμού και την δημιουργία σταθερών μορίων
Κατά το σχηματισμό του Η2 δύο πηγάδια δυναμικού έρχονται κοντά το ένα στο άλλο. Τα ηλεκτρόνια έχουν την δυνατότητα να μεταπηδήσουν από το ένα πηγάδι στο άλλο γιατί δέχονται έλξη και από τον δεύτερο πυρήνα. Αυτή η επιπλέον έλξη τροποποιεί το δυναμικό του συστήματος και των ενεργειακών του καταστάσεων σεσχέση με πριν

Τα ηλεκτρόνια του ομοιοπολικού χημικού δεσμού βρίσκονται υπό την επίδραση δυο ελκτικών κέντρων. Για να πραγματοποιηθεί αυτός ο δεσμός πρέπει τα ηλεκτρόνια του δεσμού να αντικαταστήσουν το ενεργειακό φράγμα των δυο μονών ενεγειακών "πηγαδιών" (κβαντικά φράγματα) που υπάρχει για το κάθε ένα από αυτά πριν τον δεσμό και να βάλουν στην θέση τους ενα διπλό ενεργειακό φράγμα κβαντικό . ΟΙ νέες στάθμες ενέργειας είναι η Ε1 +δε (διεγερμένη) και η Ε2-δε (βασική)
Υπάρχουν και άλλες εφαρμογές αλλά ξεφεύγουν από τους στόχους του παρόντος
Το να προχωράμε πέρα από την κλασσική Φυσική, είναι σαν να βγαίνουμε έξω από μια χώρα που κατέχουμε. Απο δω και πέρα ο στόχος και ο προορισμός ,είναι οτιδήποτε μπορεί να δει το μάτι μας και να αιστανθεί η ψυχή μας. Οι σκοποί μας βέβαια δεν είναι η υποταγή της απώτερης γνώσης και η προσαρμογή της ανώτερης σοφίας, στις ανάγκες και τις φιλοδοξίες μας. Είναι η πνοή που με αυτήν γεννηθήκαμε, είναι η έμφυτη περιέργεια που μας σπρώνει να μετέχουμε, με την αντίληψη και την κατανόηση, στο Μέγα Έργο της φύσης και τους πάνσοφες αλλα και απλές αρχές που την συνθέτουν.

Δημητρα Σπανού
ΠΗΓΕΣ
ΚβαντομηχανικήΙ Στέφανος τραχανάς
Φυσική Γ Λυκείου
https://www.physics4u.gr/articles/2002/schrodingerequation.html
https://users.auth.gr/massen/KMIII/KM-III-book.pdf
https://www.physics.ntua.gr/~farakos/QuantumMechanics2/Kef2QM.pdf
https://gate.iesl.forth.gr/~kafesaki/Modern-Physics/lectures/modern_physics7.html
https://el.wikipedia.org/wiki/Κυματοσυνάρτηση
https://el.wikiversity.org/wiki/Γενική_Χημεία
https://el.wikipedia.org/wiki/Αρχή_της_απροσδιοριστίας
https://www.physics4u.gr/articles/2002/schrodingerequation.html
Φυσική Γ Λυκείου
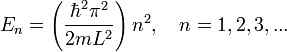 ιδιοτιμες στην ενέργεια σωματιδίου
ιδιοτιμες στην ενέργεια σωματιδίου


 .
. 
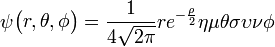 .
.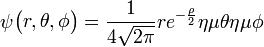 .
.