Η Ιστορία των φυσικών Επιστημών Μέρος Έκτο Η θεωρία του Χάους
της Δήμητρας Σπανού καθηγήτριας χημικού και μητέρας
Eadem mutata resurgo
(Θα προκύψει το ίδιο αν αλλάξει)
από τον Jacob Bernoulli
στον Μιχαήλ
και σε ότι αγαπάει
Η επιστήμη του 20ου αιώνα θα παραμείνει στην μνήμη των ανθρώπων για τρια μόνο πράγματα:την σχετικότητα, την κβαντομηχανική και το χάος...
Η σχετικότητα κατέρριψε τον απόλυτο χώρο και χρόνο, η κβαντομηχανική το νευτώνιο όνειρο μιας ελεγχόμενης διαδικασίας μέτρησης και το χάος τη Λαπλασιανή φαντασία της ντετερμινικής δυνατότητας για πρόβλεψη (από το ΧΑΟΣ μια νέα επιστήμη του James Gleick)
Η επιστήμη του χάους προέκυψε από την αδυναμία σε υπολογισμούς που είναι εξαιρετικά ευαίσθητοι από τις αρχικές συνθήκες
Μικρές αλλαγές στα αίτια μπορούν να επιφέρουν τεράστιες αλλαγές στα αποτελέσματα.
Η ανάγκη της επιστήμης αυτής προέκυψε από την αδυναμία των υπολογιστών να παρακολουθήσουν ορισμένα φαινόμενα . Συνήθως οι παρατηρήσεις τους ακολουθούσαν παράλληλες τροχαιές που απομακρίνονταν στην πορεία και έδιναν μεγάλες διαφορές στα αποτελέσματα.
Τέτοιοι υπολογισμοί μπορεί να αφορούσαν την πρόβλεψη του καιρού, την παρακολούθηση των κυμάτων, τις περιδυνίσεις των υγρών, την μελέτη των κινήσεων του εκκρεμούς, όταν επιδρούν σε αυτό παράγοντες όπως η αντίσταση από τον αέρα. Αλλά και σε άλλες περιπτώσεις όπως η πρόβλεψη της συμπεριφοράς των νευρώνων του ανθρώπινου εγκεφάλου στην βιολογία ή η συμπεριφορά μεγάλων πληθυσμών ανθρώπων, ή οι μοριακές χημικές αντιδράσεις ή οι παλμοί της καρδιάς ή τα λέιζερ, και οι ισορροπίες των οικοσυστημάτων
Η συμπεριφορά του χάους ισχύει τόσο στην κίνηση των γαλαξιών, όσο και στα σχέδια πάνω στο κέλυφος ενός σαλιγκαριού





στην περιδύνηση των όγκων του νερού σε έναν τυφώνα αλλά και την πορεία των λέιζερ αλλά και στον τρόπο που φυτρώνουν τα φύλλα μιας φτέρης έτσι που να δίνουν
μια όχι κανονική κανονικότητα .
Τελικά ,
Σε φαινόμενα που συνδέονται με αδυναμία πρόβλεψης κινητικής συμπεριφοράς και αδυναμία επανάληψης του ίδιου ακριβώς φαινόμενου ,ι αδυναμία υπολογισμού των αρχικών συνθηκών, αδυναμία περιγραφής με μαθηματικές εξισώσεις συναντάμε το χάος
Η πιθανή ερμηνεία αυτής της αδυναμίας είναι, ότι εκτός από τους ρητούς αριθμούς που χρησιμοποιούνται στην μαθηματική περιγραφή ενός φαινομένου υπάρχουν και οι άρρητοι αριθμοί. Εδώ βρίσκεται η αδυναμία να γνωρίζουμε και να συμπεριλαμβάνουμε τα άπειρα ψηφία των άρρητων αριθμών στις αρχικές συνθήκες και αυτό δίνει σε ορισμένες περιπτώσεις μεγάλη απόκλιση στα αποτελέσματα.
Παράδειγμα1
μικρή αλλαγή του Χ από 1.01 σε 0.99, και τι μπορεί να κάνει μέσα σε 10 βήματα
1.012=1.0201. Παίρνουμε τη νέα τιμή του Y=1.0201 και την βάζουμε στο X, οπότε θα

Διάγραμμα αριθμητικής εξομοίωσης μιας (μόνο) μεταβλητής του Lorentz στο οποίο οι αρχικές συνθήκες διαφέρουν κατά 0,0001. Στα αρχικά στάδια οι δυο καμπύλες συμπίπτουν , όχι όμως και στην εξέλιξή τους
Το χάος είναι πολύ πιο συχνό από ότι νομίζουμε. Δεν τα συναντάμε μόνο στην κίνηση των σύννέφων, των γαλαξιών, των κυμάτων ή των ηλιακών καταιγίδων αλλά είναι συχνά και στην καθημερινότητά μας, όπως η κινηση της κρέμας όταν ανακατεύεται μέσα στον καφέ στον καπνό από το τσιγάρο το νερό που τρέχει στροβιλίζεται, σχηματίζει σταγόνες ή κύματα που σκάνε σε μιαν ακτή .
Ας παρακολυθήσουμε σταγόνες νερού να κυλούν σε μια επιφάνεια.

Απειροελάχιστες διαφορές σε κάποιο μόριο της κάθε μιας σταγόνας ή απειροελάχιστες αμιχές της επιφάνειας, ή κάποια μόρια σκόνης που είναι κολημένα στην επιφάνεια, ή οι ελάχιστες πιθανές μεταβολές στις τριβές από τον αέρα, κάνουν την κάθε μια από αυτές τις σταγόνες να ακολουθεί μια εντελώς ιδιαίτερη διαφορετική πορεία που είναι δύσκολο να περιγραφεί ακόμα και από εξελιγμένους υπολογιστές.. Όμως κατά τα άλλα όλες μοιάζουν να κυλούν με τον ίδιο τρόπο.
Η αστάθεια προκαλεί το χάος
Τις τελευταίες δεκαετίες επιστήμονες όπως ο Έντουαρτ Λορεντζ ο Τζέιμς Γιόρκ ο Ρόμπερτ Μάυ ο Φίλιπ Μάρκους και άλλοι μελέτησαν φαινόμενα όπου εμφανίζεται συμπεριφορά χάους.
Ένοιωσαν προφανώς μια δυσάρεστη έκπληξη οι επιστήμονες που διαπίστωσαν αρχικά, ότι η ντετερμινιστική αντίληψη ( όταν το αποτέλεσμα εξαρτάται από την αιτία) της περιγραφής των φαινομένων δεν ίσχυε πάντα και οι γραμμικές μαθηματικές εξισώσεις που περιγράφουν διάφορα φαινόμενα δεν έδιναν πάντα αποτελέσματα.
Μελετώντας όμως αυτά τα φαινόμενα που εμφανίζονται σε διάφορα επιστημονικά πεδία και με ποικίλες εφαρμογές, έγιναν διάφορες παρατηρήσεις προσπαθώντας να κατανοήσουν την χαώδη συμπεριφορά.
Βασικό συμπέρασμα που βρήκε είναι ότι αυτό που προκαλεί το χάος είναι η αστάθεια
Αργότερα βέβαια διαπίστωσαν πως ο ντετερμινισμός και η τυχαία μεταβολή, όχι μόνο δεν αποκλείουν η μια την άλλη αλλά συνυπάρχουν και η συνύπαρξή τους αποτελεί νόμο της φύσης
Όμως, όταν αρχικά ήρθαν σε επαφή με το χάος, την στιγμή που ακόμα ήταν νωρίς για να μπορούν να αντιληφθούν, τι υπάρχει στην πραγματικότητα και να έχουν κάποια ιδέα και κάποια συμπεράσματα, ένιωσαν μάλλον άβολα. Η κατάσταση κατ αρχήν θα μπορουσε να χαρακτηριστεί σαν
μη γραμμικότητα .


Κάποιοι αντιλήφθηκαν την μη γραμμικότητα κάπως έτσι
Μη γραμμικότητα σημαίνει ότι η διαδικασία της εξέλιξης του φαινόμενου έχει έναν τρόπο να μεταβάλει τους κανόνες
Αλλά είναι επίσης αυτή που εισάγει νέες μορφές
Σημειώθηκαν τα διαφορετικά είδη της μη κανονικότητας, ερευνήθηκε το χάος σε διάφορα επιστημονικά πεδία,
Το χάος μπόρεσε να ενώσει διαφορετικά επιστημονικά πεδία των λεγόμενων ανθρωπιστικών και μαθηματικών επιστημών γιατί έγινε αντιληπτή και αναγκαία η εισαγωγή του, τόσο στις ανθρωπιστικές όσο και στις μαθηματικές επιστήμες. Δηλαδή χρειάζεται για παράδειγμα τόσο στις τηλεπικοινωνίες όσο και στην φιλοσοφία που στην προσπάθειά τους να ερμηνεύσουν την μεταβολή μιας διαδικασίας καταφεύγουν στην θεωρία του χάους
Σήμερα έχει μπει πλέον σε πολλές επιστήμες σαν ένα επιπλέον κεφάλαιο
Ενώ το χάος ενοποιεί την μελέτη διαφορετικών συστημάτων, ( για να περιγράψουμε τον καιρό έχουμε συστήματα όπως η τριβή του κινούμενου αέρα, και νερού, η διάχυση της θερμότητας στον εξωτερικό χώρο, η σταθερή επίδραση της ηλιακής ενέργειας) , μέσα από την αδυναμία πρόβλεψης και την ....η άτακτη συμπεριφορά των απλών συστημάτων , ενεργούσε πολλές φορές σαν δημιουργική διαδικασία, γενούσε πολυπλοκότητα, πλούσια οργανωμένες δομές, άλλοτε ευσταθείς κι άλλοτε ασταθείς, κάποτε πεπερασμένες και κάποτε άπειρες, αλλά πάντοτε με την μαγεία των ζωντανών πραγμάτων... ( Χάος Μια νέα επιστήμη J. Gleick)
Όταν περιγράφουμε την δομή των μορφών χρειάστηκαν να εισαχθούν νέα σχήματα που ξέφευγαν απο τα γνωστά της Ευκλείδιας Γεωμετρίας
όπως δαντελωτό, κουβαριαστό, σχισματικό, στριμμένο. Νέα στοιχεία επίσης για να περιγράφουν την κίνηση όπως φρακτάλ, διακλαδώσεις, διαλείψεις, αναδιπλώσεις και χρησιμοποιούμε την Γεωμετρία των fractals


 στην δομή των πρωτεινών συναντάμε σχήματα χάους
στην δομή των πρωτεινών συναντάμε σχήματα χάους
φρακτάλ και αναδιπλώσεις
Τα στοιχεία για να παραχθούν τα fractals αυτά τα πολύπλοκα σχήματα είναι οι αλγόρυθμοι, ενώ στην Ευκλείδια Γεωμετρία είναι οι ευθείες , οι κύκλοι, οι σφαίρες. Η θεωρία του Χάους και η Γεωμετρία των fracals συνδέονται και η μελέτη τους είναι δυνατή μόνο με την χρήση υπολογιστών. Βρέθηκαν νέες ειδικές τεχνικές για τη χρήση υπολογιστών στην μελέτη του χάους
Έχει το χάος νόμους;
- Η ανακάλυψη ότι το χάος μπορεί να έχει κάποιους κανόνες , ώστε κανείς να διακρίνει τάξη μέσα στην αταξία, μια ήταν μια άποψη που δημοσιεύτηκε σε έγκυρο επιστημονικό δημοσίευμα από τον York με τον τίτλο " Η περίοδος Τρία Συνεπάγεται Χάος¨". Μαζύ με τον Smale αλλά και πολλούς σοβιετικούς επιστήμονες που ερευνούσαν παράλληλα το ίδιο θέμα συνειδητοποίησαν πως σε κάποιες περιπτώσεις μπορούσαν να έχουν προβλέψιμα αποτελέσματα απλά έπρεπε να λάβουν υπ΄όψη την αλλαγή της περιόδου στην εμφάνισής τους. Προσπάθησαν να μεταφέρουν στην επιστημονική κοινότητα την σπουδαιότητα και το νόημα αυτής της αποκάλυψης.
- Στο χάος οι φυσικοί νόμοι χάνουν το κλασσικό τους νόημα των συμπαντικών και αναλλοίωτων και άχρονων. Εξαρτώνται εδώ από το βέλος του χρόνου και έτσι παίζουν διαφορετικό ρόλο στο παρελθόν και στο μέλλον .
- Είναι γνωστή η επιθυμία και η προσπάθεια κορυφαίων επιστημόνων όπως ο Αινστάιν, ο Hawking , που είχε γίνει γνωστή σαν την θεωρία των ενοποιημένων πεδίων, να αποκαλυφθεί ένας φυσικός νόμος από τον οποίο θα προέκυπταν όλοι οι άλλοι , με αποτέλεσμα να έρθει και η ενοποίηση όλων των αλληλοεπιδράσεων και να επιλυθεί κάθε απορία και φυσικά οι απορίες που προκύπτουν από την διερεύνηση του χάους
- Το αντίθετο του χάους δεν είναι η τάξη, αλλά η αρμονία, η ευταξία, ή ευρυθμία. Το αντίθετο της αταξίας είναι η τάξη. Κάποιος που δεν αντέχει την αταξία δεν μπορεί να επιφέρει τάξη. Το χάος είναι Άλλο πράγμα. Στην καρδιά του Χάους, στον πυρήνα του επικρατεί Αρμονία, Ευρυθμία. Επομένως όποιος δεν αντέχει το χάος, δεν μπορεί να επιφέρει αρμονία. (Αυτόχθονες Έλληνες)
Από αυτές τις επίμονες προσπάθειές τους αναδύθηκε το Χάος σαν μια νέα επιστήμη
Σύντομο ιστορικό
Πρώτος (με εξαίρεση τον Πουανκαρέ στις αρχές του 20 ου αιώνα) ο Λορεντζ ( Edward Lorenz) στο Τεχνολογικό Ινστιτούτο της Μασσαχουσέτης (ΜΙΤ ) το 1960, ασχολήθηκε με έρευνες πάνω στην μετεωρολογία και την πρόγνωση του καιρού που βέβαια δεν είναι δυνατόν να περιγραφούν με ακρίβεια δηλαδή με τους γνωστούς τρόπους και τις μαθηματικές εξισώσεις (όπως θα έπρεπε να συμβαίνει) .
Για τον Λόρεντζ, Η πρόγνωση του καιρού ίσχυε μόνο για 2-3 μέρες και μετά άρχιζε να έχει μεγάλες αποκλίσεις.
Ανάλογη δυσκολία στην μαθηματική τους περιγραφή συνάντησε στην συνέχεια όταν μελέτησε την μεταφορά θερμότητας μέσω ενός θερμαινόμενου υγρού που ανέβαίνει 
στην δεκαετία του 1970 ( στην οποία λειτουργούν ταυτόχρονα η θερμότητα και η τριβή) αυτές οι συμπεριφορές εμφανίζονται πολύ πιο συχνά απο ότι νομίζουμε εμφανίζεται η συμπεριφορά του χάους
Γενικά υπάρχει η ιδέα ότι για να έχουμε χαοτικές συμπεριφορές είναι απαραίτητο να έχουμε μεγάλο πλήθος παραγόντων ή σωματιδίων.
Αυτό όμως δεν ισχύει . Χαοτική συμπεριφορά μπορεί να εμφανιστεί ακόμα και σε μικρό αριθμό σωματιδίων

Η κλασσική μηχανική περιγράφει συμπεριφορές κινούμενων αντικειμένων και ράβδων ελατηρίων χορδών ρευσών ηλεκτρικών κυκλωμάτων κ.λ.π.. Τα μαθημαικά εφαρμόζονται και περιγράφουν αυτές τις κινήσεις επακριβώς. Όμως κανείς δεν έδωσε την πρέπουσα σημασία στο γεγονός ,ότι σε πολλά από αυτά τα φαινόμενα αυτά δεν αρκούν οι γραμμικές εξισώσεις για την περιγραφή τους αλλά χρειάζοναι και άλλες μη γραμμικές.
Ακόμα οι επιστήμονες που είχαν ασχοληθεί με το χάος είχαν ανακαλύψει δομές σε αυτήν την φαινομενικά τυχαία συμπεριφορά
Δύο επιστήμονες και δυο επιστημονικά πεδία που έδωσαν πολλά ώστε να ξεπεραστούντα αδιέξοδα και να προχωρήσει η επιστήμη αυτή
Τα δυναμικά πεδία και η τοπολογία
Ένας χαρισματικός όσο και ιδιόρυθμος Γάλλος μαθηματικός και θεωρητικός φυσικός των αρχών του περασμένου αιώνα από τους τελευταίους πανεπιστήμονες ο Ζυλ Ανρί Πουανκαρέ  ...ο μόνος που θα μπορούσε να δώσει μαθηματική αναπαράσταση σχετικά με τους νόμους της κίνησης και ο πρώτος που κατάλαβε τη δυνατότητα του χάους...
...ο μόνος που θα μπορούσε να δώσει μαθηματική αναπαράσταση σχετικά με τους νόμους της κίνησης και ο πρώτος που κατάλαβε τη δυνατότητα του χάους...
Μελέτησε αρχικά την συνδυασμένη κίνηση των τριών ουρανίων σωμάτων Ηλιου, Γης και Σελήνης και διαπίστωσε αδυναμία στην ακριβή πρόβλεψη των θέσεών τους. Πόσο μάλλον αν επεκτείνουμε και προσπαθήσουμε να υπολογίσουμε την τροχαιά του Πλούτωνα . Η συνδυασμένη επίδραση 8 άλλων πλανητών και του ήλιου κάνει την πρόβλεψη της κίνησής του αδύνατη .
Σε συστήματα ουρανίων σωμάτων διαπίστωσε μια απρόβλεπτη μη γραμμική συμπεριφορά και είδε πρώτος από όλους την δυναότητα του χάους σε δυναμικά συστήματα
.Είχε κατανοήσει ότι μικρές αλληλοεπιδράσεις μπορούν να μεγενθυνθούν λόγω ανάδρασης.
Διατύπωσε την άποψη ότι "Μια ελάχιστη αιτία που διαφεύγει της προσοχής μπορεί να προκαλέσει ένα σημαντικό αποτέλεσμα
Δεκαετίες αργότερα όταν είχε ήδη εξελιχθεί η τοπολογία (κλάδος των μαθηματικών) ο Στέφεν Σμέιλ (Stephen Smale)
 μαθηματικός από το από το Πανεπιστήμο Του Μπέρκλευ της Καλιφόρνιας , όπου αφού είχε ασχοληθεί πολύ με την επίλυση προβλημάτων τοπολογίας πολλών διαστάσεων, πήρε βραβείο Νόμπελ για τις μελέτες του πάνω σε ιδιότητες των σωμάτων που παραμένουν αμετάβλητες όταν τα σχήματα παραμορφώνονται, με τάση, στρέψη ή συμπίεση. Εδώ δεν ενδιαφέρει το σχήμα που σηνήθως αλλάζει αλλά οι ιδιότητες π.χ. αν έχει κόμπους ή τρύπες, αν είναι συνεκτικό κ.α.
μαθηματικός από το από το Πανεπιστήμο Του Μπέρκλευ της Καλιφόρνιας , όπου αφού είχε ασχοληθεί πολύ με την επίλυση προβλημάτων τοπολογίας πολλών διαστάσεων, πήρε βραβείο Νόμπελ για τις μελέτες του πάνω σε ιδιότητες των σωμάτων που παραμένουν αμετάβλητες όταν τα σχήματα παραμορφώνονται, με τάση, στρέψη ή συμπίεση. Εδώ δεν ενδιαφέρει το σχήμα που σηνήθως αλλάζει αλλά οι ιδιότητες π.χ. αν έχει κόμπους ή τρύπες, αν είναι συνεκτικό κ.α.
 το πέταλο του Stephen Smale δίνει παραμορφώσεις στον χώρο
το πέταλο του Stephen Smale δίνει παραμορφώσεις στον χώρο
Από ο 1960 άρχισε να ασχολείται με δυναμικά συστήματα και προσπάθησε να έχει μια σφαιρική αντίληψη των θεμάτων του
Στις εξισώσεις του με τις οποίες περιγράφονται δυναμικά συστήματα επιτρέπει σε ορισμένες παραμέτρους να ορίζονται από την αρχή για παράδειγμα η εσωτερική τριβή σε ένα σύστημα μετάδοσης θερμότητας
 Σε αυτό οφείλεται η σύνδεση της τοπολογίας με τα δυναμικά συστήματα
Σε αυτό οφείλεται η σύνδεση της τοπολογίας με τα δυναμικά συστήματα
πράγμα που επιτρέπει να χρησιμοποιούνται σχήματα και αυτό βοηθά να σχηματιστεί μια σαφής εικόνα της συμπεριφοράς ενός συστήματος

Επειδή έχουμε ένα πολύ δυσνόητο και εξειδικευμένο θέμα θα αρκεστούμε στην παρακάτω αναφορά, που αναφέρεται στην σύνδεση της τοπολογίας με τα δυναμικά συστήματα όπως εμφανίζονται στην φύση
....αναδεικνύεται η ευρηματικότητα της φύσης να χρησιμοποιεί, σε κάθε περιοχή φυσικών φαινομένων, τον αντίστοιχο «αλγόριθμο» και την «κατάλληλη δυναμική.
Δομές Έκλυσης
Η μη αντιστρεψιμότητα του χρόνου, αντικείμενο μελέτης και διαφωνιών φυσικών και φιλοσόφων, είχε μελετηθεί ήδη από ον 19ο αιώνα από τον Boltzmann κατά την μελέτη των νόμων της θερμοδυναμικής που κατά την μελέτη της θερμικής κίνησης σωματιδίων είχε υποστηρίζει την μη ανατρεψιμότητα  ο αριθμός των σωματιδίων στα δυο δοχεία εξισορροπείται και αυτό δείχνει την μη ανατρεψιμότητα
ο αριθμός των σωματιδίων στα δυο δοχεία εξισορροπείται και αυτό δείχνει την μη ανατρεψιμότητα
Το παρελθόν είναι χαμηλή εντροπία και το μέλλον είναι υψηλή εντροπία, και γι αυτό σύμφωνα με τον δεύτερο νόμο της θερμοδυναμικής "ο χρόνος δεν γυρίζει πίσω"
Έτσι το σύστημα έλκεται στην δεύτερη κατάσταση που την λέμε δομή έλκυσης

 Ο ελκυστής του Λόρεντζ: Ένας τρόπος να παρουσιάσουμε οπτικά την χαοτική κίνηση ή οποιαδήποτε άλλη κίνηση, είναι η κατασκευή ενός διαγράμματος φάσης της
Ο ελκυστής του Λόρεντζ: Ένας τρόπος να παρουσιάσουμε οπτικά την χαοτική κίνηση ή οποιαδήποτε άλλη κίνηση, είναι η κατασκευή ενός διαγράμματος φάσης της
Ένας τρόπος να παρουσιάσουμε οπτικά την χαοτική κίνηση ή οποιαδήποτε άλλη κίνηση, είναι η κατασκευή ενός διαγράμματος φάσης της κίνησης....
Το σύστημα τελικά εκτελεί την ίδια κίνηση για όλες τις αρχικές καταστάσεις σε μια περιοχή γύρω από την κίνηση, σχεδόν σαν να έλκεται το σύστημα σε αυτή την κίνηση (Θεωρία του χάους. Ελκυστές Βικιπαίδεια)
Πολύ αργότερα διάσημοι φυσικοί όπως ο Feyman και αργότερα ο Αινσατάιν και ο Hawkings εξετάζουν περιπτώσεις ανατρέψιμης δυναμικής κατά τις οποίες τα παραπάνω δεν ισχύουν και ο μη ανατρέψιμος χρόνος είναι μόνο μια ψευδαίσθηση
και αυτός ο εκμηδενισμός του βέλους του χρόνου έγινε δεκτό με ενθουσιασμό από κορυφαίους φυσικούς
Βέβαια το πρόβλημα της κατανόησης του χρόνου είναι πολύ παλιό και παρά τις συνταρακτικές θέσεις των φυσικών του 20ου αιώνα , καμμιά γνώση δεν επιβεβαίωσε την ισοδυναμία μεταξύ δημιουργίας και καταστροφής, ή την ταύτιση μεταξύ ενός φυτού που βλασταίνει, ανθίζει και μαραίνεται και σε ένα φυτό που πεθαίνει και επιστρέφει στον σπόρο του
Η ανάγκη της επαναφοράς της ροής του χρόνου συμπίπτεί με την γέννηση μεγάλων γεγονότων στην ιστορία του κόσμου

όπως για παράδειγμα η γέννηση του σύμπαντος και η εμφάνιση της ζωής
Βέβαια όπως έχουμε ήδη αναφέρει μέσα στο χάος δημιουργούνται νέες δομές ασταθείς ή ευσταθείς
 παράθυρα τάξης μέσα στο χάος
παράθυρα τάξης μέσα στο χάος
και ίσως η παραπάνω σκέψη, για την μη ανατρεψιμότητα του χρόνου - και από τον Boltzmann αλλά και από τους εκάστοτε φιλοσόφους και εμπειριστές-, να αναφέρεται συγκεκριμένα για τις περιοχές αυτές , μια εκ των οποίων είναι και ο χώροχρονος στον οποίο βρίσκεται το σύμπαν μας . Με την προυπόθεση βέβαια να ατενίσουμε την γέννηση και ύπαρξη του σύμπαντος μέσα στο οποίο ζουμε, σκεπτόμαστε και καταλήγουμε, σαν μια περιοχή τάξης μέσα στο χάος
Από την θέση αυτή μπορούμε ακόμα και να θυμηθούμε, όσα έχουμε ίσως ακούσει κατά καιρούς, για ύπαρξη και άλλων κόσμων πλην του δικού μας
Περιοχές των αλλαγών φάσεων
Όπως ήταν αναμενόμενο στην συνέχεια το ενδιαφέρον στρέφεται στην μελέτη των περιοχών που έχουμε αλλαγή των φάσεων όπου περνάμε από μια χαώδη φάση σε μια άλλη περιοχή τάξης
Κατά τον Ησίοδο Χάος σημαίνει το χάσμα και όχι, αταξία,.jpg)
Η γενικότερη ιδέα όπως καταλαβαίνουμε ήταν ότι οι αλλαγές των φάσεων στην χαώδη μακροσκοπική μπορουν να ερευνηθούν με παρατήρηση στην συμπεριφορά των μικροσκοπικών λεπτομερειών.
Πολλές έρευνες στρέφονται στις αλλαγές των φάσεων μεταξύ υγρού αερίου, το πέρασμα μή αγώγιμου υλικού στο αγώγιμο ή από το μη μαγνητικό στο μαγνητικό από την άμορφη ύλη στην κρυσταλλική μορφή κ.α., ελπίζοντας να βρούν εκεί ορισμένες απαντήσεις στο θέμα τους. Θεωρητικοί και πειραματικοί όπως ο Σοβιετικός Lev D Landau μετά από μελέτες, για το πέρασμα υγρών από την ομαλή ροή στον στροβιλισμό, καταλήγει πως πρόκειται για συσσώρευση διαφορετικών αλληλοεπιρρεαζόμενων , ανταγωνιστικών, συχνοτήτων,
O Amerik;ano Harry Swinney  εμπνευσμένος από ον Μαρευ τζελ -Μαν που πίστευε ότι πρέπει να ερευνηθούν οι αλλαγές καταστάσεων (αέριο σε υγρό, μη μαγνητικό σε μαγνητικό, αγωγό σε υπεραγωγό) μελετά στη συνέχεια τις μετεβολές στην θερμική αγωγιμότητα διοξειδίου του άνθρακα στο κρίσιμο σημείο όπου ο ατμός μετατρέπεται σε υγρό και παίρνει μια 1000πλάσια μεταβολή πράγμα που δεν ήταν αναμενόμενο .
εμπνευσμένος από ον Μαρευ τζελ -Μαν που πίστευε ότι πρέπει να ερευνηθούν οι αλλαγές καταστάσεων (αέριο σε υγρό, μη μαγνητικό σε μαγνητικό, αγωγό σε υπεραγωγό) μελετά στη συνέχεια τις μετεβολές στην θερμική αγωγιμότητα διοξειδίου του άνθρακα στο κρίσιμο σημείο όπου ο ατμός μετατρέπεται σε υγρό και παίρνει μια 1000πλάσια μεταβολή πράγμα που δεν ήταν αναμενόμενο .
Ο Gunter Ahlers στο Νιου Τζέρσευ μελετά την υπέρρευστη μετάβαση στο υγρό ήλιον,
Στα μέσα της δεκαετίας του 70 επισήμονες όπως ο Rierre Berge, Jerry Gollub, MarzioGiglio, Gunter Ahlers, Harry Swiinney, μελετούν την συμπεριφορά της ύλης "εκεί που ισσορροπεί στο χείλος του γρεμού".
ήδη από ις αρχές ου 20ου αιώνα είχε παρατειρηθεί στην υδροδυναμική, μια μεταβολή στην ποιότητα της κίνησης, με μαθημαικούς όρους ένα σημείο διακλάδωσης.
Το 1973 ο απόφοιτος του Χάρβαρτ ο Τζέρρυ Γκολλουμπ με δική του πρωτοβουλία ενωσε τις δυνάμεις του με τον Harry Swiinney για μια ακόμα σημαντική μελέτη στην ροή των ρευστών ανάμεσα σε περιστρεφόμενους κυλίνδρους που κόπηκε πριν ολοκληρωθεί.
Ο David Ruelle στην συνέχεια, προσπαθεί να κάνει πιο συγκεκριμένο, το άνοιγμα που είχε γίνει από τους φυσικούς που μελετούσαν τις μεταβάσεις ανάμεσα στις φάσεις και χρησιμοποίησε την γλώσσα των μαθηματικών.
στην συνέχεια, προσπαθεί να κάνει πιο συγκεκριμένο, το άνοιγμα που είχε γίνει από τους φυσικούς που μελετούσαν τις μεταβάσεις ανάμεσα στις φάσεις και χρησιμοποίησε την γλώσσα των μαθηματικών.
Αντί για το πλήθος των συσσωρευόμεων συχνοτήτων του Lev D Landau υποστήριξε πως αρκούν τρεις μόνο ανεξάρτητες κινήσεις για να δώσουν τέτοια φαινόμενα. Από το σύνολο της δουλείς του εντυπωσίασε περισσότερο, μια εικόνα που έδωσε και που οι συγγραφείς ονόμασαν παράξενο ελκυστή.
Χαρακτηρίστηκε αργότερα μια από τις σημαντκότερες επινοήσεις στην σύγχρονη επιστήμη
...Όταν το σύστημα τελικά εκτελεί την ίδια κίνηση για όλες τις αρχικές καταστάσεις σε μια περιοχή γύρω από την κίνηση, σχεδόν σαν να έλκεται το σύστημα σε αυτή την κίνηση, τότε έχουμε έναν ελκυστή. ΄Οταν η χαοτική συμπεριφορά λαμβάνει χώρα πάνω σε έναν ελκυστή αυτό το έχουν ονομάσει παράξενο ελκυστή (Θεωρία του χάους. Παράξενοι Ελκυστές Βικιπαίδεια)
Δηλαδή ο παράξενος ελκυστής "ζει" στον χώρο των φάσεων που προσφέρει δυνατότητα μετατροπής των αριθμών σε εικόνες - πληροφορίες ενός κινούμενου συστήματος
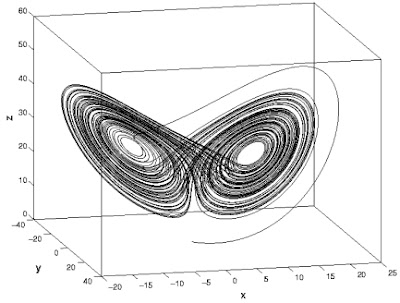
Οι παράξενοι ελκυστές μπορούν να αποδωθούν οπτικά με διαγράμματα φάσεων
Ο πρώτος και διάσημος παράξενος ελκυστής ήταν αυτός του Λορένζ το 1963. Είναι το πρώτο από τα δυο παραπάνω σχήματα ( τα διιάσημα πια φτερά της πεταλούδας) και παριστάνει την χαοτική περιστροφή ενός υγρού στην μετάδοση της θερμότητας, όπου όταν η αυξανόμενη θερμότητα έσπρωχνε το υγρό προς την μια κατεύθυνση, η τροχαιά παρέμενε στο δεξιό φτερό. Όταν σταματούσε και ακολουθούσε αντίστροφη πορεία, η τροχαιά περνούσε στο απέναντι φτερό. Ήταν ευσταθής γιατί είχε λίγες (τρεις) διαστάσεις και δεν ήταν περιοδικός γιατί έγινε παραδεκτό ότι ένας παράξενος ελκυστής πρέπει να εκπληρεί ορισμένες προδιαγραφές .
- Να έχει λίγες διαστάσεις
- Να μην είναι περιοδικός. Δηλαδή να μην διασταυρώνονταί οι τροχαιές του. Αν συμβαίνει το αντίθετο τότε η κατάσταση επιστέφει σε ένα αρχικό σημείο που σημαίνει ότι η κίνηση θα πρέπει να επαναληφθεί με τον ίδιο τρόπο έχουμε δηλαδή περιοδική κίνηση, αλλά όχι ελκυστή.
- Οι βρόγχοι και οι σπείρες πρέπει να έχουν απεριόριστο βάθος χωρίς ποτέ να συναντιούνται ή να τέμνονται.
- Επίσης να παραμένουν αυτοί οι άπειροι δρόμοι μέσα σε έναν πεπερασμένο χώρο και η γραμμή να έχει άπειρο μήκος
- Να είναι ευσταθείς και αν για κάποιο εξωτερικό λόγο ταράσσεται η κίνηση για ένα διάστημα, αυτή σταδιακά να επανέρχεται στον ελκυστή
 χιονονιφάδα Koch . Αν θελήσουμε να μερήσουμε την περίμετρο αυού του φρακτάλ σχήματος που παριστάνει μια νιφάδα χιονιού, θα βρούμε διαφορετικά αποτελέσματα αν χρησιμοποιήσουμε μια πρώη, δεύτερη ή πολλοστή διαίρεση της κάθε πλευράς κατά το σχήμα. Έτσι για άπειρες διαιρέσεις το μήκος αυτό γίνεται άπειρο.
χιονονιφάδα Koch . Αν θελήσουμε να μερήσουμε την περίμετρο αυού του φρακτάλ σχήματος που παριστάνει μια νιφάδα χιονιού, θα βρούμε διαφορετικά αποτελέσματα αν χρησιμοποιήσουμε μια πρώη, δεύτερη ή πολλοστή διαίρεση της κάθε πλευράς κατά το σχήμα. Έτσι για άπειρες διαιρέσεις το μήκος αυτό γίνεται άπειρο.
Κατά τον David Ruelle όταν μελετούσε την στροβιλώδη ροή, η απώλεια ενέργειας σε μια στροβιλώδη ροή, πρέπει να οδηγεί σε ένα είδος συστολής του χώρου των φάσεων, σε μια έλξη προς έναν ελκυστή ο οποίος δεν πρέπει να είναι σταθερό σημείο γιατί η ροή θα κατέληγε σε ακινησία. Μια τροχαιά που τραβούσε όλες τις άλλες γειτονικές τροχαιές.
Στην δουλεία του μαζύ με τον Τάκενς εκδόθηκε το 1971 ένα επιστημονικό άρθρο που συμπεριέλαβε και αυτό του Λορένζ το 1963 που με την βοήθεια υπολογιστών και τον ελκυστή του ο οποίος εφόσον ήταν τριών διαστάσεων έπρεπε να κινούνται οι σπειροειδείς γραμμές του σε δυο επιφάνειες όπου όταν αυτές τέμνονταν οι σπείρες δεν θα έπρεπε να διασταυρωθούν. Αυτό γίνονταν πραγματικά γιατί όταν οι σπείρες πρωχωρούσαν να ενωθούν, οι επιφάνειες απομακρύνονταν κι έτσι δεν τέμνονταν ποτέ.
Η ονομασία Θεωρία του Χάους οφείλεται στον μαθηματικό Jαmes Yorke το 1975 που ήδη σε νεαρή ηλικία συνεργάστηκε και εγινε στην συνέχεια επικεφαλής στο Ινστιτούτο Φυσικής Επιστήμης και Τεχνολογίας του Πανεπιστήμιου του Μέρυλαντ

Δούλεψε πάνω στις εργασίες του Λορεντζ και του Σμέιλ και σαν μαθηματικός έδωσε την δική του οπτική με άρθρο που δημοσίευσε στο πιο έγκυρο επιστημονικό περιοδικό και είχε τον τίτλο " Η περίοδος Τρία Συνεπάγεται Χάος¨" γιατί μετά από επίπονες προσπάθειες κατάληξε ότι με τον τριπλασιασμό της περιόδου ενός αντίστοιχου φαινόμενου εμφανίζεται το χάος στην συμπεριφορά του

στον τριπλασιασμό όπως βλέπουμε στο τρίτο διάγραμμα εμφανίζονται δυο διαφορετικά επίπεδα και το συστημα γίνεται χαοτικό
Τελικά ο Γιόρκ δηλώνει: Το χάος είναι πανταχού παρόν, είναι ευσταθές και έχει δομή.

σε ένα διχαλωτό διάγραμμα στην αρχή οι διακλαδώσεις εμφανίζουν περιοδικότητα, στην συνέχεια αρχίζει το χάος με μη κανονικές περιόδους και μέσα στο χάος εμφανίζονται "παράθυρα" με περιττές περιόδους. Εμφανίζεται δηλαδή η περίοδος 3 που διπλασιάζεται (3,6,12) και ξανά πάλι το χάος
Ο Γιόρκ μίλησε στον φίλο του Ρόμπερτ Μάυ (Robert May) Αυστραλό θεωρητικός φυσικός και μαθηματικός, ο οποίος υπήρξε επικεφαλής των επιστημονικών συμβούλων της κυβέρνησης του Ηνωμένου Βασιλείου , ο Πρόεδρος του η Royal Society , [2] και καθηγητής στο Σίδνεϊ και του Πρίνστον

Στην φαση αυτή κι ενώ το ενδιαφέρον για την θεωρία του χάους γίνεται εντονότερο οι προσπάθειες γίνονται περισσότερο συντονισμένες και μοιάζουν να ακολουθούν δυο δρόμους. 1. Η προσπάθεια να παρουσιαστούν και οπτικά οι παράξενοι ελκυστές και 2. Η πειραματική δουλειά και μέσα από αυτήν ο έλεγχος και η ολοκλήρωση της θεωρίας αυτής
Οι εφαρμογή του χάους μπήκε στην βιολογία, μελετώντας την συμπεριφορά πληθυσμών, στην διάρκεια του χρόνου. Στην συνέχεια δοκίμασαν την θεωρεία του χάους σε μοντέλα πληθυσμών διαφόρων ειδών, που είδε ανάλογα αποτελέσματα. Οι πληθυσμοι εάν η παράμετρος που δοκίμαζε είχε χαμηλή τιμή, το μοντέλο καταστάλαζε σε σταθερή κατάσταση πληθυσμού, εάν είχε μεγάλη τιμή η σταθερότητα μπορούσε να εξαφανιστεί και ο πληθυσμός να ταλαντώνεται σε δυο τιμές εναλλασσόμενες. Εάν οι τιμές γίνονταν πολύ μεγάλη τότε το σύστημα φαινόταν να συμπεριφέρεται με απρόβλεπτο τρόπο
Πέρα από την άνθιση της επιστήμης του χάους σε ΗΠΑ και Ευρώπη Σοβιετικού επιστήμονες εργάζονται παράλληλα με πολύ καλά αποτελέσματα
Στην Ιαπωνία επιστήμονες ό πως ο Yoshisuke Ueda οδήγησαν στην ανακάλυψη ενός συνόλου παράξενων ελκυστών μέσα από την μελέτη των ηλεκτρικών κυκλωμάτων
Στην Γερμανία ο γιατρός Otto Rossler οδηγήθηκε στους παράξενους ελκυστές μέσα από τον δρόμο της χημείας και της θεωρητικής βιολογίας
Από ένα σύστημα απλών εξισώσεων που κατασκέυασε ο Otto Rössler το 1976 χρησιμοποιώντας απλούς μη-γραμμικούς όρους. Ενδεικτικά για να πάρουμε μια ιδέα για το τι μπορεί να σημαίνει αυτό πρόκειται για τις παρακάτω εξισώσεις

 Ο παράξενος ελκυστής δείχνει την χαωτική συμπεριφορά ενός ρώτορα όταν το εκκρεμές εκτελεί ταλάντωση ωθούμενη από διεγέρτη.
Ο παράξενος ελκυστής δείχνει την χαωτική συμπεριφορά ενός ρώτορα όταν το εκκρεμές εκτελεί ταλάντωση ωθούμενη από διεγέρτη.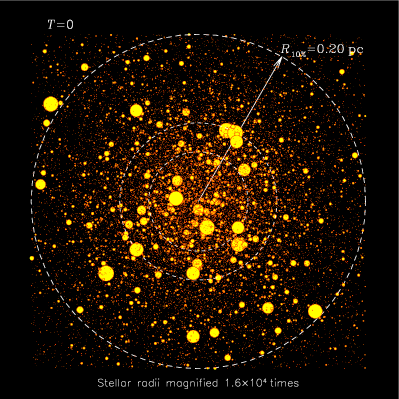 και έφτασε στο συμπέρασμα πως ο πυρήνας του σμήνους μπορούσε να αποκτήσει τεράστια κινητική ενέργεια και να περάσει σε κατάσταση άπειρης πυκνότητας. Αφού δουλεψε αρκετά χρόνια έφτασε να δώσει μια τεχνική τρισδιάστατων απεικονήσεων που έχει της λογική των τροχαιών που δεν τέμνονται ποτέ. Φαντάστηκε ένα όρθιο επίπεδο στην μια πλευρά του Γαλαξία και οι τροχαιές να περνούν από αυτό
και έφτασε στο συμπέρασμα πως ο πυρήνας του σμήνους μπορούσε να αποκτήσει τεράστια κινητική ενέργεια και να περάσει σε κατάσταση άπειρης πυκνότητας. Αφού δουλεψε αρκετά χρόνια έφτασε να δώσει μια τεχνική τρισδιάστατων απεικονήσεων που έχει της λογική των τροχαιών που δεν τέμνονται ποτέ. Φαντάστηκε ένα όρθιο επίπεδο στην μια πλευρά του Γαλαξία και οι τροχαιές να περνούν από αυτόΣτην δεκαετία τουστο Εθνικό εργαστήριο του Λος Αλάμος ο Μίτσελ Φαιγκενμπάουμ αναλαμβάνει επιστημονικός διευθυντής και αφου κάνει αναδιάρθρωση στους συνεργάτες που δούλευαν εκεί, προσέχοντας να έχουν το θεωρητικό υπόβαθρο στην σωματιδιακή φυσική και κβαντική θεωρία πεδίου.
Αντιλαμβάνονται την σημασία μιας δομής στην θεωρία του κβαντικού πεδίου που είναι γνωστή σαν
ομάδα επανακανονικοποίησης (renormalization group)
Μελετώντας την συμπεριφορά της ύλης, όταν μεταπηδά από την μια κατάσταση στην άλλη, προσπάθησαν να κατανοήσουν τις αλλαγές της και είπαν πως τα μικροσυστατικά της ύλης (άτομα, μόρια, κυψελίδες κ.λ.π.)καθώς έχουν εγκαταλείψει μια κανονική κατάσταση επικοινωνούν μεταξύ τους ,μέσω των γειτονικών τους στοιχείων, και ανταλλάσσοντας πληρφορίες καθώς μεταβαίνουν από την ενδιάμεση σε μια άλλη κανονική κατάσταση και πρέπει να "αποφασίσουν και να καταλήξουν" για συμπεριφορά τους. Ώστε να επανακανονικοποιηθούν.
Γι αυτές τις θεωρίες ο Kenneth Wilson πήρε βραβείο Nobel το 1982 και μαζύ με δυο άλλους φυσικούς, τον Leo Kadanoff και τον Michael Fisher βοήθησαν σημαντικά την θεωρία του χάους.
ΠΗΓΕΣ
ΧΑΟΣ ΜΙΑ ΝΕΑ ΕΠΙΣΤΗΜΗ James Gleick
Οι νόμοι του χάους Ilya Prigogine
https://el.wikipedia.org/wiki/%CE%98%CE%B5%CF%89%CF%81%CE%AF%CE%B1_%CF%84%CE%BF%CF%85_%CF%87%CE%AC%CE%BF%CF%85%CF%82
https://bioenergynews.capitalblogs.gr/showArticle.asp?id=10942&blid=210
https://el.wikipedia.org/wiki/Ανρί_Πουανκαρέ
https://greekphysics.wordpress.com/2010/10/20/εικασία-πουανκαρέ/
https://www.hdml.gr/pdfs/journals/1469.pdf
https://petridis58.blogspot.com/2011/05/o-ilya-prigogine.html
https://el.wikipedia.org/wiki/Θεωρία_του_χάους
https://autochthonesellhnes.blogspot.no/2014/12/blog-post_66.html
https://iomikron.blogspot.no/2011/07/blog-post_16.html
ακατέργαστο

αναφέρεται και το συγγενές πεδίο της φυσικής που λέγεται Κβαντική θεωρία του Χάους και μελετά μη αιτιοκρατικά συστήματα σύμφωνα με τους νόμους της Κβαντομηχανικής.

