Αρχική Σελίδα > Η Ιστορία των Φυσικών Επιστημών. Μέρος Πέμπτο. Πέρα από την Κλασσική Φυσική Ι. Η κβάντωση των φυσικών μεγεθών: Πληρώνει ο Θεός με δόσεις;

Η Ιστορία των Φυσικών Επιστημών. Μέρος Πέμπτο. Πέρα από την Κλασσική Φυσική Ι. Η κβάντωση των φυσικών μεγεθών: Πληρώνει ο Θεός με δόσεις;

2014-12-25 21:41

της Δήμητρας Σπανού καθηγήτριας Χημικού

ΠΡΙΝ ΑΠΟ ΤΗΝ ΚΒΑΝΤΙΚΗ ΘΕΩΡΙΑ ΤΗΣ ΥΛΗΣ

Στο γύρισμα του περασμένου αιώνα η Κλασσική Φυσική, του Νεύτωνα και του Λαπλάς έμοιαζε να έχει φτάσει σην ολοκλήρωσή της.

Κάποια στιγμή φαινόταν ότι μπορούσε να δώσει όλες τις απαντήσεις και να επιλύσει κάθε είδους πρόβλημα.

Όμως σε εκείνη την περίοδο , από την κορυφή που μόλις είχε φτάσει η Επιστήμη, φάνηκε στο βάθος η νέα κορυφή

Εκείνη της περιγραφής του κόσμου του μικρόκοσμου.

Βέβαια η στατιστική μηχανική, είχε κάνει ήδη μια πολύ καλή προσπάθεια που όμως δεν αποδείχτηκε αρκετή

Η Κλασσική Φυσική χωρίζεται σε τρεις θεμελιώδεις κλάδους

1.Την Kλασσσική μηχανική

που με την θεωρία του Νεύτωνα (F=m.a) μπορεσε να περιγράψει την κίνηση, όχι μόνο των σωμάτων πάνω σην γη αλλά και των πλανητών

και την κυματική θεωρία που περιγράφει την συμπεριφορά των μηχανικών κυμάτων ( ${ \partial^2 u \over \partial t^2 } = c^2 \nabla^2 u$ )

2.Την Κλασσική θεωρία των πεδίων

Η έννοια του πεδίου δυνάμεων εδώ έχει νόημα μόνο για δυο θεμελιώδη πεδία δυνάμεων το βαρυτικό και το ηλεκτρομαγνητικό

Νόμος Παγκόσμιας Έλξης που διατυπώθηκε από τον Νεύτωνα και που περιγράφει τις δυνάμεις στο βαρυτικό πεδίο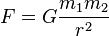 $F = G \frac{m_1 m_2}{r^2}$

Νόμος του Κουλόμπ που περιγράφει τις δυνάμεις στο ηλεκτρικό πεδίο $F_c=k\frac{|q_1\cdot q_2|}{r^2}$

στην συνέχεια τα φαινόμενα του ηλεκτρισμου συνδέονται με τα μαγνητικά φαινόμενα και περιγράφεται η θεωρία του ηλεκτρομαγνητισμού από τις 4 εξισώσεις του Maxwell

παραπομπή:

Η ιστορία των Φυσικών Επιστημών . Μέρος τρίτο: Hλεκτρομαγνητική ακτινοβολία. Η ανακαλυψή της ελευθέρωσε τον άνθρωπο από τα καλώδια τόσο, που άρχισε να νοιώθει ότι δεν υπήρχε πια, τίποτα να τον σταματήσει, να επιχειρήσει οτιδήποτε στο μέλλον

3.Την Κλασσική Στατιστική Μηχανική

Μπόρεσε να προσεγγίσει συμπεριφορά των πολυπληθών σωματιδίων του μικρόκοσμου

και να συνδέσει την συμπεριφορά τους με μακροσκοπικά φαινόμενα όπως η Πίεση , η θερμοκρασία κ.α.

Χωρίς να χρειαστεί να περιγράψει ξεχωριστά την συμπεριφορά του καθενός από αυτά, χρησιμοποιόντας μόνο στατιστικά στοιχεία για την πιθανότητες εύρεσής τους σε διάφορες θέσεις ή την κατανομή τους σε διάφορες ταχύτητες , βγαίνουν υπολογισμοί και μαθηματικές φόρμουλες ώστε να υπολογίσουμε μακροσκοπικά μεγέθη του μακρόκοσμου -στον οποίο ανήκουν τα σωμαίδια αυτά- όπως η Πίεση , η θερμοκρασία και άλλα που προκύπτουν στην συνέχεια.

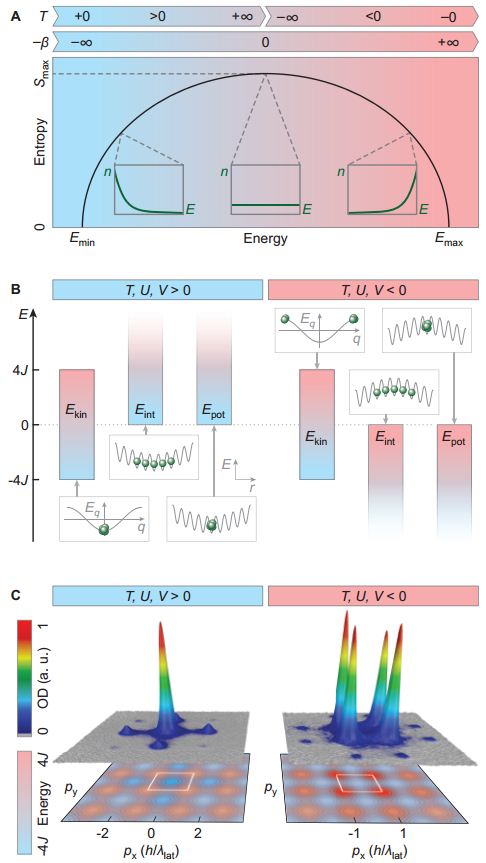
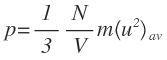
Εδώ για παράδειγμα είναι οι Τύποι που δίνει την πίεση τον Όγκο και την θερμοκρασία ιδανικού αερίου σε σχέση με τον αριθμό των μορίων του

Ν είναι ο αριθμός σωματιδίων u η ταχύτητα των σωματιδίων (Νόμος Γκέι-Λουσάκ)

και στην συνέχεια διατυπώνονται οι σχέσεις μεταξύ πίεση και θερμοκρασίας ιδανικών αερίων σε μακροσκοπική προσέγγιση δηλαδή που να αφορά τον κόσμο μας αυτόν που αντιλαμβανόμαστε και που μπορούμε να μετρήσουμε.

Ακόμα με την Στατιστική Μηχανική, μπορουμε να αποδώσουμε και άλλες φυσικές έννοιες όπως την εντροπία που μας δίνει την αταξία των συστατικών ενός συστήματος . Η εντροπία (που δίνει το μέτρο της αταξίας και της αποδιοργάνωσης των σωματιδίων) , δίνεται από τον στατιστικό ορισμό

όπου W είναι αριθμός των συνδυασμών των σωματιδίων με τους οποίους μπορεί να πραγματοποιηθεί μια κατανομή.

Η Εντροπία δεν αναφέρεται ούτε και μπορεί να προσδιοριστεί με τους όρους της Κλασσικής Μηχανικής

Αυτά είναι λοιπόν τα βασικά θέματα της Κλασσικής Φυσικής

Η Θεωρία της Σχετικότητας παρά την επαναστατική αλλαγή

που έφερε αποτελεί τμήμα της Κλασσικής Φυσικής.

Βέβαια ορισμένα μέρη της Κλασικής Φυσικής χρειάζονται σχετικιστική τροποποίηση και η Σχετικότητα αποτελεί το γενικό πλαίσιο μέσα στο οποίο πρέπει να προσαρμοστούν οι νόμοι της.

$m = m_{0} / \sqrt{1-v^{2} / c^{2}}$

μετασχηματισμοί του Lorentz Ολλανδός κορυφαίος θεωρητικός φυσικός1853-1928

Στην Γενικευμένη Θεωρία της Σχετικότητας ,

Ανάλογος μετασχηματισμός γίνεται και στο βαρυτικό πεδίο . Το σχετιστικό βαρυτικό πεδίο μοιάζει με το ηλεκτρομαγνητικό δηλαδή διαδίδεται στον κενό χώρο με την ταχύτητα του φωτός και γίνεται αποδεκτή η ύπαρξη βαρυτικών κυμάτων.

Ο διισμός της ύλης

Έτσι και το βαρυτικό πεδίο συμπεριλαμβάνεται στα θέματα της Κλασσικής Φυσικής που ξεχωρίζει τις δυο φυσικές οντότητες: τα σωματίδια και τα πεδία.

Τα πρώτα είαι εντοπισμένα με συγκεκριμένη συμπεριφορά ενώ στα πεδία τα χαρακτηριστικά τους εκτείνονται στον χώρο

Οι έννοιες σωματίδιο και πεδίο είναι αλληλοαποκλειόμενες

Δηλαδή η φύση χρησιμοποιεί δυο φορείς ενέργειας τα υποθέματα και τα πεδία

Στην σχετικιστική θεωρία , ο ρόλος του πεδίου καθορίζεται από το έλλειμα ενέργειας και ορμής, που υπολογιζεται , όταν δυο σωματίδια ( ή φορτία) κινούνται το ένα ως προς το άλλο. Οι μεταβολές σε μεγέθη όπως η ορμή και η ενέργεια του καθενός από αυτά δεν είναι ακαριαίες (ώστε να διατηρούνται σταθερές οι ολικές τιμές αλλά παρουσιάζουν χρονική διαφορά. Η διαφορά οφείλεται ότι η αλληλοεπίδραση του ενός προς το άλλο δεν γίνεται ακαριαία αλλά φτάνει με μια ταχύτητα (αυτήν του φωτός ή κάποια άλλη) . Έτσι καθυστερεί η προσαρμογή στις νέες συνθήκες με τις νέες τιμές αυτών των μεγεθών

Αυτό το έλλειμμα ενέργειας φέρεται από το κύμα του πεδίου που έτσι το κύμα αποκτά πραγματική φυσική υπόσταση.

υπήρχαν και εκείνοι οι φιλόσοφοι που υποστήριζαν τη συνύπαρξη της Ύλης και του Νοητού ως συστατικά στοιχεία της ουσίας των αισθητών πραγμάτων. Οι φιλόσοφοι αυτοί με πρωτοπόρους και πιο σημαντικούς τον Πλάτωνα και τον Αριστοτέλη

Αυτό όμως έχει καθοριστικές συνέπειες, δηλαδή κάνει ασαφή την διάκριση μεταξύ των δυο θεμελιωδών εννοιών σωματίδιο και πεδίο. Έτσι κατά κάποιον τρόπο "ανοίγουν οι ασκοί του Αιόλου" και δεν υπάρχει πλέον κανένας κανόνας που να απαγορεύει να συμπεριφέρονται τα σωματίδια σαν κύματα και τα κύματα σαν σωματίδια. (έτσι είπαν τότε)

όμως κάπου εδώ κάνει την εμφάνισή της η Κβαντική Θεωρία με τον Mαx Plank

για να διαπιστώσουμε ( καθώς η θεωρία αυτή ξεδιλπώνεται) πως και τα δυο αυτά φυσικά μεγέθη (κυματα και σωματίδια) είναι κβαντισμένα.

Η ΚΒΑΝΤΙΚΗ ΘΕΩΡΙΑ ΤΗΣ ΥΛΗΣ (ΓΕΝΙΚΑ)

ο Max Plank αποδεικνύει ότι η ακτινοβολούμενη ενέργεια δεν είναι συνεχής,

αλλά μεταφέρεται σε διακριτές ποσότητες (κβάντα) το 1900

Η αρχή της Κβαντικής θεωρίας

Κβάντο είναι

1. Η ελαχίστη διακριτή ενέργεια ακτινοβολούμενη από τα άτομα ενός υλικού

2.Στοιχειώδης μονάδα μέτρησης ενός φυσικού μεγάθους που λαμβάνει διακριτές τικές

(Βικιλεξικό)

Ο πρώτος που διατύπωσε την κβαντική θεωρία ήταν ο Max Plank το 1900

Max Plank γερμανός Φυσικός από το Πανεπιστήμειο του Βερολίνου και κάτοχος βραβείου Νόμπελ (1858-1947)

ΣΤΑ ΥΛΙΚΑ ΣΩΜΑΤΑ

Ο MAX Plank αξιοποίησε τις πειραματικές μετρήσεις συναδέλφων του πειραματικών φυσικών γύρω από τα φάσματα εκπομπής αερίων από τις οποίες , έβγαινε το συμπέρααμα ότι η ακτινοβολία δεν ήταν συνεχής αλλά ορισμένων συγκεκριμένων συχνοτήτων

Κατέληξε , ότι η μετατροπή της θερμικής ενέργειας σε ακτινοβολία δεν μπορεί να γίνει σε οποιανδήποτε ποσότητα. Υπάρχει μια στοιχειώδης ποσότητα και η ποσότητα ενέργειας που μετατρέπεται κάθε φορά από την μια μορφή στην άλλη πρέπει να είναι πολλαπλάσιο. της στοιχειώδους αυτής ποσότητας. Κατέληξε σε μια παράμετρο που

η μεταφερόμενη ενέργεια μέσω ακτινοβολίας μπορεί να πάρει κάθε φορά μόνο τις επιτρεπτές τιμές που να είναι πολλαπλάσιες του h

Το h .

Η μεταφερόμενη ενέργεια είναι συνάρτηση της εκάστοτε συχνότητας της ακτινοβολούμενης ενέργειας και οι τιμές που μπορεί να πάρει είναι συγκεκριμένες και πάντα πολλαπλάσια της ακτινοβολούμενης συχνότητας επί την σταθερά h .

Λέμε δηλαδή ότι η ακτινοβολία που εκπέμπει ένα αέριο σώμα είναι κβαντισμένη

και ο τύπος Ε=h.v είναι από τους πιο σημαντικούς τύπους του 20ου αιώνα και σημαοδοτεί την γέννηση της Κβαντικής Θεωρίας και Θέτει τις βάσεις για να ολοκληρωθεί αργότερα το 1915

Όπως αποδείχθηκε αργότερα με αντίστοιχο τρόπο πως,

η ποσότητα της ακτινοβολίας που απορροφά ένα αέριο σώμα για την μετατρέψει σε θερμότητα, σε χημική ενέργεια, σε άλλης συχνότητας ακτινοβολία , σε ηλεκτρική ενέργεια κ.λ.π. είναι επίσης κβαντισμένη

Η κβάντωση στην απορρόφηση ενέργειας έχει καθοριστική σημασία για την δομή και την σταθερότητα του κόσμου μας.

O Alvert Einstein εισηγείται την ύπαρξη κβάντου ακτινοβολούμενης ενέργειας (φωτόνιο)

Η κβαντική θεωρία ολοκληρώθηκε με την "Υπόθεση των φωτονίων" από τον Einstein το 1905

με το φωτοηλεκτρικό φαινόμενο που το περιέγραψε σαν κβαντική διαδικασία

Επανεξετάζοντας την "υπόθεση Πλανκ" και επεκτείνοντας αυτή και στη διαδικασία της απορρόφησης, ερμηνεύει έτσι το φωτοηλεκτρικό φαινόμενο, πρότεινοντας την ύπαρξη "κβάντων φωτός", δηλαδή φωτονίων.

Τα φωτόνια όπως κάθε σωματίδιο, όταν προσπίπτει σε ένα μέταλλο αποδίδει ένα μέρος από την ενέργειά του για να "ξεκολήσει "το ηλεκτρόνιο να υπερπηδήσει το φράγμα της δυναμικής Ενέργειας (επίσης φαινόμενο Κβάντωσης)

Στην συνέχεια το συγκεκριμένο ηλεκτρόνιο, μπορεί να κινηθει και να δόσει ηλεκτρικό ρεύμα με Κινητική Ενέργεια ώστε να ισχύει

hf= K_max + Φ. όπου Φ είναι το έργο εξαγωγής Κ η κινητική ενέργεια του ηλεκτρονίου και f η συχνότητα του προσπίπτοντος φωτονίου και h η σταθερά του Plank

( Βικιπαίδεια)

Η σωματιδιακή φύση των φωτονίων επιβεβαιώνεται πειραματικά από τον Arthour Compton το 1924

Ο Arthur ComptonΑμερικάνος Φυσικός (1892-1962) βραβείο Νόμπελ 1927

Ανέφερε στο γνωστό πείραμα Compton ότι η ηλεκτρομαγνητική ακτινοβολία εμφανίζει φαινόμενα σκέδασης όταν προσπέσει (συγκρουστεί ) με φορτισμένα σωματίδια (ηλεκτρόνια). Αυτό αποδεικνύει την σωματιδιακή φύση των ηλεκτρονίων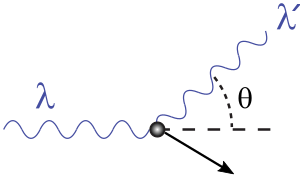

Η ΕΦΑΡΜΟΓΗ ΤΗΣ ΚΒΑΝΤΙΚΗΣ ΘΕΩΡΙΑΣ ΣΕ ΑΤΟΜΙΚΕΣ ΚΑΙ ΜΟΡΙΑΚΕΣ ΔΟΜΕΣ (ΑΡΧΙΚΗ ΠΡΟΣΕΓΓΙΣΗ)

Η κβάντωση της ενέργειας των ηλεκτρονιακών στοιβάδων και της θέσης της τροχαιάς της περιστροφής τους

κατά την κατασκευή των ατόμων

Ο Neils Bohrs το 1913

διατυπώνει την θεωρία της κβάντωσης στην κατασκευή των ατόμων και εισάγει τον n (κύριος κβαντικός αριθμός)

Neils Bohr Δανός φυσικός (1885-1962)

Εξετάζουμε την κβάντωση στην ενέργεια και την ακτίνα της τροχαιάς για κάθε ηλεκτρόνιου του ατόμου

Ισχύει ότι, η ενέργεια που έχουν και η ακίνα της τροχαιάς τους, είναι κβαντισμένα μεγέθη.

Εικόνα

Το ατομικό πρότυπο του Neils Bohr και η ενέργεια της κάθε στοιβάδας του

Ο αριθμός που καθορίζει την κβάντωση είναι ο n=1,2,3,4... που ονομάζεται κύριος κβαντικός αριθμός. Το φυσικό νόημα αυτού είναι, ότι με αυτόν καθορίζεται η απόσταση του κάθε ηλεκτρονίυ από τον πυρήνα αλλά και η ενέργειά του.

Για την ενέργεια:

Αν πάρουμε για παράδειγμα το απλουστερο άτομο , αυτό του υδρογόνου όπου οι 4 πρώτες ενεργειακές στάθμες έχουν ενέργεια που δίνεται από τον τύπο Ε=h.ν με αντικατάσταση υπολαγίζουμε την ενέργεια σις 4 πρώτες

Για να διεγερθεί ένα ηλεκτρόνιο και να περάσει από την πρώτη θεμελιώδη και χαμηλώτερης ενέργειας στάθμη με n=1 και ενέργεια -13,6eV στην δεύτερη χρειάζεται ενέργεια ίση με την διαφορά τους δηλαδή 10,2eV ενώ από την δεύτερη στην τρίτη(2,18.10^-18 joule) ενώ από την δεύτερη στην τρίτη 1,89 eV σύμφωνα με την διαφορά ενέργειας μεταξύ των δύο

Δηλαδή για να ξεφύγει από την θεμελιώδη και σαθερή κατάσταση που βρίσκεται συνήθως πρέπει να απορροφήσει το μεγαλύτερο ποσό ενέργειας, πολύ μεγαλύτερο από αυτό που χρειάζεται για να περάσει από την δεύτερη στην τρίτη κι ακόμα πιο μεγάλο από όσο χρειάζεται για να περάσει από την τρίτη στην τέταρτη στάθμη. Είναι λοιπόν δύσκολο και χρειάζεται την μεγαλύτερη ενέργεια για να ξεφύγουν τα άτομα και κατ επέκταση όλα τα υλικά σώματα από την θεμελιώδη και σταθερή κατάσταση , όπως τα ξέρουμε συνήθως. Η απορροφούμενη ακτινοβολία πρέπει να είναι μιας συγκεκριμένης συχνότητας σύμφωνα με την θεμελιώδη εξίσωση των κυμάτων E=h.ν

από όπου προκύπτει ότι η συχνότητα του φωτονίου που απορροφάται κάθε φορά για την διέγερση του ηλεκτρονίου ενός ατόμου βρίσκεται κάτω από αυστηρούς περιορισμούς, Εδώ για παράδειγμα να είνα ΔΕ/h ν= 1,54.10¹⁶Hz όπου η ΔΕ είναι Ε₂-Ε₁θεμελιώδους και πρώτης διεγερμένης

Για την θέση του ηλεκτρονίου:

Παρατηρούμε πως η στροφορμή του ηλεκτρονίου είναι μέγεθος κβαντισμένο και είναι ακέραιο πολλαπλάσιο της ποσότητας , όπου h είναι η σταθερά του Plank.

$\mathbf{L}=mur= {nh \over 2\pi}$ $\mathbf{n}=1,2,3,...$ Τ

ο μέτρο της στροφορμής του περιστρεφόμενου ηλεκτρόνιου δίνεται από την σχέση L=m u r και από εδώ βρίσκουμε επίσης και την ακτίνα της τροχαιάς r=L/mu όταν πάρουμε υπ΄όψη την κβάντωση της στροφορμής

Κβάντωση παρατηρείται και στην απόσταση από τον πυρήνα (ακτίνα τροχαιάς προς το παρόν ) που μπορεί να κινούνται τα ηλεκτρόνια ενός οποιουδήποτε πια ατόμου.

(Αργότερα το 1927 καταρρίπτεται η στενή έννοια της κίνησης των ηλεκτρονίων σε καθορισμένη κυκλική τροχαιά γύρω από τον πυρήνα που αντικαθίσταται από την πυκνότητα πθανότητας ηλεκτρονιακού φορτίου )

τελικά όμως ισχύει πως

Τα άτομα από τα οποία δομείται η ύλη βασίζουν την κατασκευή τους στην κβάντωση της ενέργειας των ηλεκτρονιακών στοιβάδων και της απόστασης που έχει σε κάθε μια στοιβάδα από τον πυρήνα

Κβάντωση υπάρχει στην ενέργεια που έχει κάθε μια τροχαιά του ατόμου στην οποία περιστρέφονται τα ηλεκτρόνια c,2..
Η ποσότητα της ενέργειας που απορροφάται ή εκπέμπεται κατά την διέγερση ή αποδιέγερση ενός ατόμου είναι επίσης κβαντισμένες
Κβάντωση υπάρχει επίσης και στις αποστάσεις των τροχαιών περιστροφής από τον πυρήνα (προς το παρός το λέμε ακτίνα)

ΚΒΑΝΤΩΣΗ ΣΤΑ ΥΠΟΠΥΡΗΝΙΚΑ ΣΤΟΙΧΕΙΩΔΗ ΣΩΜΑΤΙΔΙΑ ΚΑΙ ΣΤΙΣ ΑΛΛΗΛΟΕΠΙΔΡΑΣΕΙς ΜΕΤΑΞΥ ΤΟΥΣ

Στην Σωματιδιακή Φυσική η κβάντωση επεκτείνεται και προτείνονται και άλλες στοιχειώδεις ποσότητες

Richard P. Feynman Richard Feynman Nobel.jpg Αμερικανός θεωρητικός φυσικός που μεταξύ άλλων έκανε την τελική διατύπωση της κβαντομηχανικής ,εισήγαγε την θεωρία της κβαντικής ηλεκτροδυναμικής και την φυσική των σωματιδίων Τιήθηκε με το βραβείο Νόμπελ ιδιαίτερα για την συνεισφορά του στην κβαντική ηλεκτροδυναμική που είναι προιόν συνένωσης της κβαντικής Μηχανικής και της ειδικής θεωρίας της σχετικότητας

Στον κόσμο των υποατομικών σωματιδίων οι στοιχειώδη σωματίδια που αποτελούν την ύλη είναι μικρότερα σε μέγεθος από τα πρωτόνια νετρόνια και ηλεκτρόνια

Λέγονται φερμιόνια και διακρίνονται σε κουάρκς (από τα οποία κατασκευάζονται τα πρωτόνια και νετρόνια) και το λεπτόνια που είναι πολύ μικρότερα και από τα τα οποία συστατικά των ηλεκτρονίων

εφ όσον τα υποατομικά σωματίδια είναι πολλαπλάσια των στοιχειωδών σωματιδίων Φερμιονίων (κουαρκς και λεπτόνια) και αυτά στην συνέχεια είναι που σχηματίζουν τα αδρόνια και τα ηλεκτρόνια. Αυτά σχηματίζουν τα άτομα τα μόρια και τελικα την ύλη.

Έτσι μπορούμε να πουμε πως η μάζα είναι μέγεθος κβαντισμένο

Κάθε σωματίδιο μπορεί να ανταλλάξει ενέργεια με ένα αντιστοιχο αντισωματίδιο. Η ενέργεια αυτή μεταφέρεται από σωματίδια-φορείς κι αυτό ισχύει για κάθε θεμελιώδη αλληλεπίδραση. Τα σωματίδια αυτά λέγονται μποζόνια- και είναι φορείς της αλληλεπίδρασης που ένα σωματίδιο ασκεί σε κάποιο άλλο (αντί). Διακρίνουμε

1. . Κβαντική Χρωμοδυναμική

Η αλληλεπίδραση η οποία ευθύνεται για τον σχηματισμό των πρωτονίων και των νετρονίων, συγκρατώντας τα κουάρκ, είναι η Κβαντική Χρωμοδυναμική

Χρησιμοποιούνται τα γλουόνια (g)( για τις αλληλοεπιδράσεις μεταξύ των φερμιονίων(κουαρκς και αντικουάρκς) στο ισχυρό πυρηνικό πεδίο)

2. Κβαντική Ηλεκτροδυναμική

Κβαντική ηλεκτροδυναμική, εκείνο δηλαδή το τμήμα της κβαντικής θεωρίας πεδίου που περιγράφει τις αλληλεπιδράσεις του φωτός με τα φορτισμένα σωματίδια.

Χρησιμοποιούνται τα φωτόνια (γ) για την ηλεκτρομαγνητική αλληλεπίδραση που παράγεται από επιταχύνσεις φορτισμένων σωματιδίων (λεπτονίων και αντιλεπτόνιων)

3. Μποζόνια W και Z

που μεσολαβούν για αλληλεπιδράσεις στο ασθενές πυρηνικό πεδίο για αλληλοεπιδράσεις μεταξύ αδρονίων (πρωτόνια, νετρόνια)

4. Η βαρύτητα

εικάζεται ότι και αυτή αλληλεπιδρά με ένα τανυστικό μποζόνιο με σπιν 2 το βαρυτόνιο για αλληλοεπιδράσεις σωματιδίων ύλης και αντιύλης (ατόμων, μορίων).

τελικά, οι αλληλοεπιδράσεις μεταξύ σωματιδίων πυρηνικές ηλεκτρομαγνητικές ασθενείς πυρηνικές και βαρυτικές είναι κβαντισμένα μεγέθη

(για τις βαρυτικές δεν είναι ακόμα απόλυτα παραδεκτό)

Στον μικρόκοσμο οι αλληλεπιδράσεις γίνονται με τα μποζόνια.

Εφ όμως μιλάμε για πολύ μεγάλο αριθμό μποζονίων το φαινόμενα μεταφέρεται στον μακρόκοσμο (κύμα, ακτινοβολία)

Σχετικά εύκολα καταλήγουμε πως η κυματική ηλεκτρομαγνητική ακτινοβολία είναι κι αυτή κβαντισμένη

Όταν Ο Max Plank είχε δώσει τον τύπο ενέργεια ακτινοβολίας Ε=h.ν και την σταθερά

μετά από μετρήσεις και υπολογισμούς φάνηκε καθαρά πως η ακτινοβολούμενη ενέργεια ήταν μέγεθος κβαντισμένο. Δεν έλαβε καθόλου υπ όψη την ύπαρξη των μποζονίων και εφ όσον η θεωρία αυτή δεν είχε ακόμα διατυπωθεί

Τελικά όμως έδινε την ενέργεια ενός μποζόνιου (του φωτόνιου ) πολλαπλασιασμένη επί τον αριθμό των φωτονίων ανά μονάδα χρόνου

και γι αυτό ήταν το κβάντο της ακτινοβολούμενης ενέργειας στον μακρόκοσμο, που είναι συνάρτηση της συχνότητας ακτινοβολίας ,δηλαδή των φωτονίων που μεταφέρουν την αλληλοεπίδραση σε συγκεκριμένο χρόνο

Στο ηλεκτρονικό περιοδικό Physics4u's Weblog σε άρθρο στις 20-9-10 με τίτλο Μήπως τα μποζόνια μεταμφιέζονται σε φερμιόνια; δημοσιεύεται το παρακάτω

.....Τα μποζόνια μπορούν να σχηματίζουν ένα ‘σωρό’ το ένα δίπλα από το άλλο χωρίς κανένα περιορισμό, ακόμα κι αν όλα καταλαμβάνουν την ίδια κβαντική κατάσταση. Σε χαμηλές θερμοκρασίες, αυτό προκαλεί περίεργα φαινόμενα, όπως η υπεραγωγιμότητα, η υπερευστότητα και το συμπύκνωμα Bose-Einstein. Επιτρέπει, επίσης, σε φωτόνια της ίδιας συχνότητας να σχηματίσουν συνεκτικές ακτίνες λέιζερ. Τα φερμιόνια, από την άλλη πλευρά, αποφεύγουν το ένα το άλλο. Τα ηλεκτρόνια γύρω από έναν πυρήνα στοιβάζονται σε φλοιούς, αντί να καταρρέουν σε ένα συμπυκνωμένο νέφος, με αποτέλεσμα να σχηματίζονται άτομα με μια μεγάλη γκάμα χημικών ιδιοτήτων.....

Μοιάζει σαν τα μποζόνια να δηλώνουν την παρουσία τους στον μακρόκοσμο ένα στάδιο πριν απο τα σωματίδια αλληλεπίδρασης , τα μποζόνια ένα εκ των οποίων είναι το φωτόνιο

β. Στις ηλεκτρομαγνητικές δυνάμεις περιγράφονται οι ισχυρές, οι ασθενείς και οι ηλεκτρομαγνητικές θεμελιώδεις δυνάμεις

ΑΛΛΑ ΦΥΣΙΚΑ ΜΕΓΕΘΗ ΣΤΑ ΟΠΟΙΑ ΕΜΦΑΝΙΖΕΤΑΙ ΚΒΑΝΤΩΣΗ ΕΙΝΑΙ:

1.το ηλεκτρικό φορτίο Q που είναι ακέραιο πολλαπλάσιο του στοιχειώδους ηλεκτρικού φορτίου

e =1,60217733 10^-19C το φορτίο του ηλεκτρονίου

2.Το νευρικό σήμα . Είναι επίσης κβαντισμένο . Η ελαχίστη ποσότητα διαφοράς δυναμικού μεταξύ δυο νευρικών κυττάρων για να υπάρξει νευρική διαβίβαση λέγεται ουδός και εξαρτάται από τα νευρικά κυκλώματα και το περιβάλλον

παραπομπή:

Το Ανθρώπινο Νευρικό Σύστημα: Μέρος Δεύτερο: Ο Ηλεκτρισμός και Χημεία είναι η μόνη γλώσσα που καταλαβαίνει το νευρικό μας σύστημα (Όπως για να γραφτεί ένα τραγούδι)

Χωρίς την κβάντωση η ύπαρξη σταθερών ατομικών δομών θα ήταν τελείως αδύνατη.

Οι φόβοι που εκφράστηκαν παραπάνω ότι δεχόμενοι τον διισμό της ύλης και του φωτός (σωματίδιο και κύμα ) και η ασαφής διάκριση των ορίων μεταξύ τους θα ανοίξει τους ασκούς του Αιόλου, περιορίζονται τώρα εφ όσον αυτή η μεταφορά ενέργειας δεν είναι ανεξέλεγκτη αλλά περιορίζεται και οριοθετείται από την κβαντική θεωρία Ακόμα γνωρίζουμε πια, πως μόνο με κβαντισμένες ποσότητες όχι συνεχείς, μπορεί να γίνει επίσης μεταφορά ενέργειας από το ένα σώμα στο άλλο .

Η θέση και η ενέργεια του κάθε ενός ηλεκτρονίου στο άτομο είναι εντελώς προσδιορισμένη από το φαινόμενο της κβάντωσης. Τα φυσικά αυτά μεγέθη είναι κβαντισμένα και αυτό έχει σαν συνέπεια,να έχουμε μια εντελώς προσδιορισμένη κατασκευή στο κάθε άτομο της ύλης

ΚΒΑΝΤΩΣΗ ΣΤΗΝ ΕΚΛΥΣΗ 'Η ΑΠΟΡΡΟΦΗΣΗ ΕΝΕΡΓΕΙΑΣ ΣΤΙΣ ΧΗΜΙΚΕΣ ΑΝΤΙΔΡΑΣΕΙΣ

Κατά τις χημικές αντιδράσεις απορροφάται ή εκλύεται ενέργεια που έχει συγκεκριμένη τιμή. Οι τιμές αυτές για κάθε αντίδραση είναι δυνατόν να υπολογιστούν είτε ανά mol ή ανά μόριο

Εάν η απορρόφηση ή απελευθέρωση ενέργειας ήταν συνεχής και όχι κβαντισμένη τα μόρια των σωμάτων θα απορροφούσαν διαρκώς ακτινιβολούμενη ενέργεια οποιασδήποτε συχνότητας με αναπόφευκτο αποτέλεσμα, οι χημικές αντιδράσεις να γινότανανεξέλεγκτα μέχρι την πλήρη διάλυση της ύλης όπως υπάρχει και σχηματίζει τον γνωστό υλικό κόσμο μας

Χωρίς την κβάντωση στην κατασκευή των ατόμων ο κόσμος δεν θα υπήρχε

και χωρίς την κβάντωση στους μετασχηματισμούς της ύλης, ο κόσμος θα διαλυόταν σε μια έκρηξη ανεξέλεγκτων χημικών αντιδράσεων

αυτή όμως η ιστορία προχωράει ακόμα πιο μακρυά

Δήμητρα Σπανού

ΠΗΓΕΣ

ΚΒΑΝΤΟΜΗΧΑΝΙΚΗ1 Στέφανος Τραχανάς

Βιβλία ΟΕΔΒ Γ Λυκείου

https://el.wikipedia.org/wiki/Νόμος_της_παγκόσμιας_έλξης

physicsgg.me176 × 25

physiclessons.blogspot.com561 × 248

thepersistenceofafreephoton.blogspot.com614 × 292

Φυσική για ποιητές Robert March

https://el.wikipedia.org/wiki/Φωτόνιο

el.wikipedia.org207 × 197

www.physics4u.gr180 × 180

www.esoterica.gr362 × 259

https://el.wikipedia.org/wiki/Φωτοηλεκτρικό_φαινόμενο

en.wikipedia.org280 × 396

https://el.wikipedia.org/wiki/Σκέδαση_Κόμπτον

www.stocklearning.gr680 × 340

www.terrapapers.com2048 × 1640

www.gataros.net835 × 835

physicsgg.me486 × 863

physiclessons.blogspot.com243 × 144

https://physicsgg.me/2013/12/05/qed-κβαντική-ηλεκτροδυναμική/

physiclessons.blogspot.com206 × 166

https://gate.iesl.forth.gr/~kafesaki/Modern-Physics/lectures/modern_physics7.html

https://codepetalouda.blogspot.gr

ακατέργαστο

Κβαντική μηχανική ή

Η κβαντομηχανική περιγράφει τη συμπεριφορά της ύλης στο μοριακό, ατομικό και υποατομικό επίπεδο.

α. η μάζα

β. οι ηλεκτρομαγνητικές δυνάμεις και

γ. οι ποσότητα αλληλεπίδρασης αυτών

επίσης το βαρυτόνιο (ή αλλιώς γκραβιτόνιο από τον αγγλικό όρο graviton) είναι το υποθετικό στοιχειώδες σωματίδιο-φορέας της βαρυτικής αλληλεπίδρασης

Κβάντωση ηλεκτρικού φορτίου λέμε το φορτίο κάθε φορτισμένου σώματος που θα είναι ακέραιο πολλαπλάσιο του στοιχειώδους ηλεκτρικού φορτίου

e =1,60217733 10^-19C το φορτίο του ηλεκτρονίου

a=e²/(2Î₀hc). Στην πραγματικότητα η τιμή της σταθεράς λεπτής υφής a είναι:1/137.0359895 (με μια αβεβαιότητα: 0,045 μέρη στο εκατομμύριο).

Φυσιολογικά, κάθε χημική αντίδραση χρειάζεται ένα ποσό ελαχίστης ενέργειας (ενέργεια ενεργοποίησης) για να ξεκινήσει να γίνεται και εάν η ποσότητα που υπάρχει διαθέσιμη, είναι κάτω από την ελάχιστη ενέργεια (κβάντο) η αντίδραση δεν μπορεί να γίνει.

Πίσω

Η Ιστορία των Φυσικών Επιστημών. Μέρος Πέμπτο. Πέρα από την Κλασσική Φυσική Ι. Η κβάντωση των φυσικών μεγεθών: Πληρώνει ο Θεός με δόσεις;

Επαφή