Οι μαγευτικοί κρύσταλλοι. Μέρος Πρώτο: Τι μπορεί να πετύχει η ύλη όταν οργανώνεται.

2014-05-11 06:42

Της Δήμητρας Σπανού ,  Χημικού, Καθηγήτριας  Β/θμιας Εκπ/σης

 Θεωρητικές σπουδές για 

Οι κρύσταλλοι πάντα τραβούσαν την προσοχή μου. Πριν κάποια χρόνια επισκευτήκαμε με τα παιδιά του 2ου Γυμνάσιου Σάμου που τότε υπηρετούσα εκεί σαν καθηγήτρια, το παλαιοντολογικό Μουσείο των Μυτηλινιών Σάμου. Εκέι υπάρχει μια πολύ όμορφη έκθεση με ορυκτά κι ανάμεσά τους υπέροχους κρυσταλλους. Σήμερα ενδιαφέρομαι ακόμα περισσότερο και σας μεταφέρω κάποια πράγματα που  έχω μάθει μέχρι τώρα για τους κρυστάλλους.

 

Σημείωση : Η μελέτη των κρυστάλλων διδάσκεται στις πανεπιστημιακές σχολές Γεωλογίας  όπως λ.χ.

287 ΓΕΩΛΟΓΙΑΣ ΠΑΤΡΑ 11647

 

 

συνεχίζουμε...

Το να μην είναι οργανωμένη η ύλη δηλαδή να βρίσκονται τα δομικά του στοιχεία σε τυχαίες θέσεις είναι κατανοητό.

 Αν θυμάμαι καλά αναλαμβάνει η στατιστική τότε να περιγράψει τις ιδιότητές τους με πολύπλοκές εξισώσεις. Η κατάσταση αυτή της ύλης ονομάζεται άμορφος και έχει την ιδιότητα της ισοτροπίας .Την συναντάμε σε πολλά στερεά βιολογικά οργανικά  υλικά και σε αρκετά ανόργανα σώματα όπως το γυαλί (βεβαίως κατ' εξοχην στα υγρα και τα αέρια σώματα)

Ισοτροπία έχουμε όταν σε κάθε κατεύθυνση δηλαδή οι μακροσκοπικές ιδιότητες της ύλης είναι ίδιες. Η πυκνότητα , η σκληρότητα , η απορρόφηση και η διάθλαση του φωτός κ.λ.π.

    

άμορφο (γυαλί)  ,  Μοριακός κρύσταλλος , Kρύσταλλος Ιοντικός,  Ατομικός κρύσταλλος  Κρυσταλλος μετάλλου

                           (ναφθαλίνη)  C10H8        αλίτης ( NaCl )             Διαμάντι ( C)               Μαγγνήσιο

Τι θα συμβεί όμως όταν τα μικροσκοπικά σωματίδια  ήτοι:

α. μόρια που συγκρατούνται μεταξύ τους με δυνάμεις Van der  Waals, (υψηλές τάσεις ατμών , χαμηλά σημεία ζέσης, συχνά εξαχνώνονται λ.χ. ναφθαλίνη) 

β. ιόντα που συγκρατούνται μεταξύ τους από ηλεκτροστατικές έλξεις, , 

γ. άτομα που συγκρατούνται με ομοιοπολικούς δεσμούς,

δ. μεταλλικά στερεά που συνδέονται με "μεταλλικούς δεσμούς"

 αρχίσουν να παίρνουν συγκεκριμένες θέσεις και να οργανώνονται       ανάλογα. Τότε αρχίζουμε να βλέπουμε τα κρυσταλλικά σώματα.

Η οργάνωση αυτή μπορεί να είναι σε μια σε δυο ή και στις  τρείς διαστάσεις 

Στοιχιση μορίων ή ιόντων σε γραμμικές δομές , 

Διαμόρφωση επιπέδων πλεγμάτων με καθορισμένη δομή

 Διαμόρφωση κρυσταλλικού πλέγματος στον χώρο.

Την εσωτερική δομή των σωμάτων μπορέσαμε να την μελετήσουμε μετά την ανακάλυψη των ακτίνων Χ  (Κρυσταλλογραφία)

Όλα αυτά δηλαδή που αναφέρθηκαν για τα πλέγματα μέχρι το 1895 ήταν μόνον θεωρείες. Το ορατό φως δεν έδεινε κανένα αποτέλεσμα σκέδασης, ανάκλασης, περίθλασης, διάθλασης πάνω στα άτομα -μόρια των κρυστάλλων, που θα επιβεβαίωνε την υπαρξη στοιχειωδών σωματιδίων και την θέση τους. Δηλαδή θα αποδείκνυε το κρυσταλλικό πλέγμα. Προφανώς το μήκος κύματος του ορατού φωτός ήταν κάπως "μεγάλο" για να ερευνήσει τον μικρόκοσμο των κρυστάλλων. Κι ενώ η θεωρία των κρυσταλλικών πλεγμάτων ανεπιβεβαίωτη κόντευε να ξεχαστεί, η ανακάλυψη των ακτίνων Χ με μήκος κύματος 5-10000 φορές μικρότερο από το ελάχιστο του ορατού φωτός  (400 έως 770 nm) ήρθε να επαληθεύσει την θεωρία.

Για να καταλάβουμε περίπου για ποιες διαστάσεις μιλάμε, στο σφαλερίτη ZnS για παράδειγμα το μόριό του έχει μάζα 97/0.606.1024gr  και η απόσταση των μορίων είναι 3,4.10-8cm  ή 3,4.10-10m περίπου. Το ορατό φως έχει μήκος κύματος 4-7,7.10-7 m ενώ οι ακτίνες Χ της τάξης 10-10m των δηλαδή της τάξης μεγέθους με τις διατομικές αποστάσεις των κρυστάλλων. Λογικό λοιπόν να υπάρξουν αποτελέσματα με αυτές.

Ο εντοπισμός των θέσεων των δομικών λίθων του κρυστάλλου με την βοήθεια των ακτίνων Χ γίνεται με την παρατήρηση των φασμάτων συμβολής των ανακλωμένων στους δομικούς λίθους ακτίνων Χ. Ίσως γνωρίζουμε ότι αν θα απόσταση των δυο πηγών (σημείων ανάκλασης) είναι ακέραιο πολλαπλάσιο του μήκους κύματος θα έχουμε αποτέλεσμα (κροσσοί συμβολής). Κάπως έτσι υπολογίζονται οι θέσεις και οι αποστάσεις στο κρυσταλλικό πλέγμα.

Ανάλογα φάσματα μπορούμε να πάρουμε για να εντοπίσουμε την θέση μικροκρυστάλλων, ή επιφανειακών στοιβάδων (όχι ατόμων, μορίων κ.λ.π.) με ακτινοβολία πολύ μεγαλύτερου μήκους κύματος (καθοδικές ακτίνες από ηλεκτρόνια λ=10-8 έως 10-10 ) αλλά αυτό βέβαια δεν αφορά ακριβώς το πλέγμα

Τότε βέβαια οι ιδιότητες παύουν να είναι ίδιες σε όλες τις κατευθύνσεις και λέμε πως έχουμε ανισοτροπία. Το φως και  οι δυνάμεις συναντούν διαφορετικό περιβάλλον και φυσική συμπεριφορά ανάλογα με την κατεύθυνσή τους μέσα στην κρυσταλλική δομή της ύλης . Εξαίρεση αποτελεί η κρυστάλλωση στο κυβικό σύστημαόπου έχουμε ισοτροπία. 

Τι σημαίνει πρακτικά η ανισοτροπία ενός σώματος; Να προσπαθεί , σαν παράδειγμα ,ένας δυνατός άντρας να κόψει (σχίσει) με ένα ειδικό εργαλείο κάποιον κρύσταλλο και να μην τα καταφέρνει και μετά ένα παιδί με το ίδιο εργαλείο να τα καταφέρει πολύ καλά. Ποια η διαφορά; Η κοπή έγινε σε διαφορετικές κατευθύνσεις. Έχει αποδειχθεί και είναι λογικό η κοπή ή το τρύπημα να συναντά λιγότερη αντίσταση αν γίνεται παρράλληλα σε μιαν έδρα ή μια ακμή του κρυστάλλου αντίστοιχα. Αλλιώς είναι δύσκολο να νικήσει κανείς τις δυνάμεις που εμφανίζονται στα κρυσταλλικά πλέγματα και κρατούν κοντά τους δομικούς λίθους. 

Ποιες είναι όμως αυτές οι θέσεις που παίρνουν οι δομικοί λίθοι στον χώρο; Οι θέσεις είναι τόσο συγκεκριμένες ώστε αν ενώσουμε τα σημεία τους θα σχηματιστούν γεωμετρικά σχήματα (χωροπλέγματα) σχεδόν απόλυτα ακριβή. Βέβαια οι αποστάσεις μεταξύ τους είναι της τάξης του 10-10μέτρα. Αυτά όμως τα σχήματα μπορούν κατά κάποιον τρόπο να αναγνωριστούν και  στις διαστάσεις που βλέπουμε, δηλαδή στις πέτρες αν είναι κατεργασμένες και γυαλισμένες. Μερικές φορές ορισμένες πλευρές είναι πιο τονισμένες από άλλες ενώ οι γωνίες ανάμεσα στις πλευρές παραμένουν ίδιες. Το φθοριούχο ασβέστιο  (Fluorite) πιο κάτω κρυσταλώνεται στο κυβικό και σε κάποιο βαθμό αυτό φαίνεται στην κοπή του.

         όπως και επόμενα που βλέπουμε.

fluorite CaF2                  βαρύτης BaSO4            ασβεστίτης CaSO4               σφαλερίτης   ZnS

(κυβικό)                           (ρομβικό)                     (τριγωνικό)                           (εξαγωνικό)

 

Παραθέτουμε κάτω σχεδιαγράμματα για ορισμένα από τα 7 τα κρυσταλλικά συστήματα (τρικλινές, μονοκλινές, ορθορομβικό, τετραγωνικό, ρομβοεδρικό, εξαγωνικό, κυβικό,). Βλέπουμε πως εξελίσεται ένα από αυτά λ.χ. το κυβικό αν στο κέντρο του γεωμετρικού σχήματος υπάρχει ένας δομικός λίθος στο κέντρο (και τότε λέγεται κεντρωμένο) ή σε όλες τις πλευρές (ολοκεντρομένο), κι αν φέρουμε τις γραμμές από το κέντρο στις κορυφές ή από τα κέντρο κάθε πλευράς στις κορυφές , μοιάζουν να δημιουργούνται νέα γεωμετρικά στερεά και αυτό φαίνεται και στην κοπή. Είναι όμως το ίδιο σύστημα.

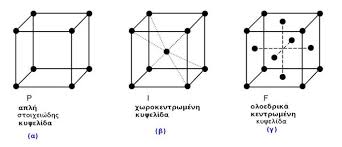
   τρεις πλεγματικοί τύποι κυβικού συστήματος

                                   Ορισμένα ακόμα συστήματα κρυστάλλωσης. Πρισματικό, τετραγωνικό, τριγωνικό,κ.α. 

Με τις διαφορόποιήσεις αυτές τα βασικά κρυσταλλικά συστήματα μπορεί να δώσουν υποκατηγορίες  (τάξεις) που ανήκουν όπως αναφέραμε στο ίδιο σύστημα. Λόγου χάρη στο κυβικό έχουμε 5 τάξεις, Την κυβική ολοεδρία, την ολοαξονική ολοεδρία, την παρημιεδρία, την ανθιμιεδρία, την τετραεδρία . Ακόμα προκύπτουν έτσι ένα πλήθος από συμμετρίες (εδώ 36 ομάδες συμμετρίας) και τρεις πλεγματικοί τύποι.

 

  Ας επανέλθουμε στα προηγούμενα και να προσπαθήσουμε να φανταστούμε πως ακριβώς τα άτομα , μόρια, ιόντα, μεταλλικα ιόντα, πλησιάζονται ώστε να δημιουργήσουν το κρυσταλλικό πλέγμα.

Ιοντικά πλέγματα: Γίνεται με τρόπο ώστε να μπορούν να ικανοποιηθούν οι ελκτικές δυνάμεις μεταξύ αντιθέτων φορτίων και να ελαχιστοποιηθούν οι απώσεις μεταξύ των ομονύμων. Λαμβάνουμε βέβαια υπ όψη τις διαστάσεις και των μεν και των δε. Τελικά το καλύτερο αποτέλεσμα έρχεται για τις ελκτικές δυνάμεις αν πλησιάσουν όσο γίνεται πιο κοντά (και ανάλογο σύστημα κρυστάλλωσης έχουν) αν είναι δυνατόν και μέχρις επαφής. Γεμίζουν όσο γίνεται τον χώρο τα ιόντα. Συνεπεια, μικρές τάσεις ατμών, υψηλά σημεία τήξεως, διαλυτά σε πολικής κατασκευής διαλύτες, διαλύματα και τήγματα καλοί αγωγοί του ηλεκτρισμού

        

    Ιοντικό πλέγμα                Ατομικό πλέγμα (γραφίτης, διαμάντι )  Μεταλλικό πλέγμα

Πλέγματα ατόμων  αντίθετα τα  που συγκρατούνται με ομοιοπολικούς δεσμούς, (αδάμας, γραφότης,ανθρακοπυρίτιο, προτιμούν την ανοικτή δομή. Δεν γεμίζουν δηλαδή όλον τον χώρο Διότι τα ομοιοπολικά τροχιακά έχουν καθορισμένες τροχαιές και επομένως υπάρχουν ενδιάμεσα κενά. Λόγω των ομοιοπολικών δεσμών στα άτομα του πλέγματος έχουμε μεγάλη σταθερότητα, υψηλά σημεία ζέσης και ελάχιστη διαλυτότητα (λόγω έλλειψης φορτίων)

Μοριακά πλέγματα που συγκρατούνται με ασθενείς δυνάμεις van der walls που οφείλονται κυρίως σε περιστροφές των ηλεκτρονίων  και έχουν σχετικά υψηλές τάσεις ατμών, χαμηλά σημεία ζέσεως και εξαερώνονται εύκολα . Τα πλέγματά τους εξαρτώνται κυρίως από την κατασκευή των μορίων. Παράδειγμα σφαιρικά και συμμετρικά μόρια συνήθως εμφανίζουν συμπαγή διάταξη και τότε δίνουν υψηλά σημεία ζέσεως σε αντίθεση με αυτά που δεν είναι συμμετρικά (κάτω)

    

    ανθρακένιο ΣΤ 217ο  C        φαινανθρένιο  ΣΤ 99,6οC      μεταλλικό πλέγμα πυκνο κυβικό και πυκνό εξαγωνικό

Γνωστό είναι και το μεταλλικό πλέγμα που άτομα μετάλλου (κατιόντα) διατάσσονται σε στρώματα ώστε  στο πρώτο τοποθετούνται τα σωματίδια και στο δεύτερο τα σωματίδια τοποθετούναι στις κοιλότητες του πρώτου επιπέδου ενώ  μεταξύ τους κυκλοφορεί το ηλεκτρονιακό νέφος έτσι ώστε μοιάζει η κατασκευή με ένα τεράστιο κρύσταλλο της μεγίστης πυκνότητας  δομής. Η δομή εξαρτάται από το είδος του μετάλλου

Τελειώνοντας λοιπόν το θέμα της συντάξεως των σωματιδίων σε δομές καταλαβαίνουμε την μεγάλη σημασία που έχει στην εμφάνιση και κυρίως τις ιδιότητες των υλικών, ο τρόπος που είναι διατεταγμένοι οι μονάδες τους και πως ισορροπούν οι μεταξύ τους δυνάμεις

ΑΛΛΟΤΡΟΠΙΑ ΠΟΛΥΜΟΡΦΙΣΜΟΣ

Πως όμως γίνεται και το ίδιο σώμα μπορεί να κρυσταλλωθεί σε περισσότερα από ένα συστήματα; (Αλλοτροπικές μορφές)  Εξαρτάται καθαρά από τις συνθήκες και από την εσωτερική του ενέργεια κάθε φορά.  Μετατροπή μιας αλλοτροπικής μορφής σε μια άλλη εκλύεται ή απορροφάται ενέργεια.

ΑΛΛΟΤΡΟΠΙΚΕΣ ΜΟΡΦΕΣ ΔΙΟΞΕΙΔΙΟΥ ΤΟΥ ΠΥΡΙΤΙΟΥ   και       ΤΟΥ ΑΝΘΡΑΚΙΟΥ ΑΣΒΕΣΤΙΟΥ             ΑΝΘΡΑΚΑ

                SiO2                                                                                                                  CaCO3

 

            

           Χαλαζίας                Τριδυμίτης                 ασβεστίτης         αραγωνίτης             διαμάντι       γραφίτης

        τριγωνικό                  εξαγωνικό                   τριγωνικό           ρομβικό                 κυβικό         εξαγωνικό

 

Ένα τελευταίο θέμα που θα δούμε είναι το πως αναπτύσσονται οι κρύσταλλοι.

Στην αρχή σχηματίζονται σε τυχαίες  θέσεις  μέσα  στο υγρό τήγμα ή διάλυμα μικρός αριθμός ατόμων συσσωματώνεται και δημιουργεί σταθερούς  πυρήνες κρυστάλλωσης,    Οι  πυρήνες  αυτοί που καποιες φορές προυπάρχουν (από ξένα σωματίδια -προσμείξεις) αποτελούν την αρχή που γύρω από αυτήν αναπτύσσεται  ο  κρύσταλλος με προσθήκη νέων ατόμων από το υλικό του κρυστάλλου σε θέσεις που προβλέπονται  από  το  κρυσταλλικό  σύστημα  αυτόύ. 
  Οι  κρύσταλλοι  αυτοί  αναπτύσσονται  με διαφορετικό  προσανατολισμό  στο  χώρο.  Καθώς  συνεχίζεται  η  στερεοποίηση δημιουργούνται  και  νέοι  πυρήνες  κρυστάλλωσης  σε  άλλες  νέες  τυχαίες  θέσεις,  ο αριθμός  των  οποίων  περιορίζεται  καθώς  η  πήξη  προχωράει.  Στις  θέσεις  όπου γειτονικοί  κρύσταλλοι  έρχονται  σε  επαφή  παύει  η  περαιτέρω  ανάπτυξή  τους  και όταν  ολοκληρωθεί  η  στερεοποίηση  οι  κρύσταλλοι  εφάπτονται  μεταξύ  τους.  Οι κρύσταλλοι  αυτοί  ονομάζονται κρυσταλλίτες ή  κόκκοι  και  οι  διεπιφάνειες  μεταξύ τους όρια  κόκκων  Το  στερεοποιημένο  σώμα  δεν  παρουσιάζει  μια συνεχόμενη  κρυσταλλική  δομή   σε  όλη  τη  μάζα   του,  οπότε  θα  μιλούσαμε   για μονοκρύσταλλο,  αλλά  αποτελείται  από  πολλούς  κόκκους,  δηλαδή  είναι  ένα πολυκρυσταλλικό υλικό.
(μεταφέρεται κείμενο  του Σ. Καλογερόπουλου, επισημάνσεις δικές μου)
 
Μετά από αυτό θα προσπαθήσω να δώσω κάποια στοιχεία για θέματα που θεωρούναι κάπως προχωρημένα για τους μη ειδικούς για το θέμα   όπως είναι η διδυμία στους κρυστάλλους, οι μεικτοί κρύσταλλοι, η συνκρυστάλλωση
Πολλές φορές υπό ειδικές συνθήκες από έναν πυρήνα μπορεί να δημιουργηθούν δύο ή περισσότεροι κρύσταλλοι σε διαφορετικές κατευθύνσεις (δυδιμία πολυδυμία) συμβαίνει σε περίπτωση διδυμίας οι κρύσταλλοι να έχουν σχέση ειδώλου /αντικειμένου και λέγονται κατοπτρικοί κρύσταλλοι
 
Μικτοί κρύσταλλοι: Μέσα στο κρυσταλλικό πλέγμα ορισμένα άτομα αντικαθίστανται από άλλα που γενικά μοιάζουν στο μέγεθος και στις ιδιότητες. Πολύ συνηθισμένο στα μεταλλικά πλέγματα.( κράμα) 
Συγκρυστάλλωση: Διπλά άλατα  σχηματίζονται συχνά όταν καθιζάνουν δυο διαφορετικά αλατα που είναι στο ίδιο διάλυμα σε ορισμένη αναλογία 

  σπινέλιο MgAl2O4 διδυμία μικτός    

  χρωμίτης FeCr2O4 μικτός       διπλό στυπτηρία KAL(SO4)2.12H2O

 

 

 Πηγές: Γενική Χημεία (Παύλου Σακελλαρίδη), Σχολικά βιβλία ΟΑΕΔ, Ακτινοσκοπία κρυστάλλων και λοιπαι φυσικαί ιδιότηται αυτών. Αναστάσιου Γεωργιάδου Καθηγητή ορυκτολογίας-πετρολογίας Παν, Αθηνών 1962, Tεχνολογία Υλικών, Τμήμα Ηλεκτρολογίας, ΤΕΙ Πειραιά  Σ. Καλογεροπούλου, Βικιπαίδεια, 

Πίσω