Η κυματική Εξίσωση: Εξίσωση ελατηρίου, μηχανική ταλάντωση χωρίς - με τριβή και με απόσβεση. Ηλεκτρικές ταλαντώσεις LC, LCR

2019-03-10 21:35

της Δήμητρας Σπανού Χημικού καθηγήτριας στο 1ο Γυμνάσιο Δάφνης

υπό κατασκευή

 

 

α. Εξίσωση ελατηρίου

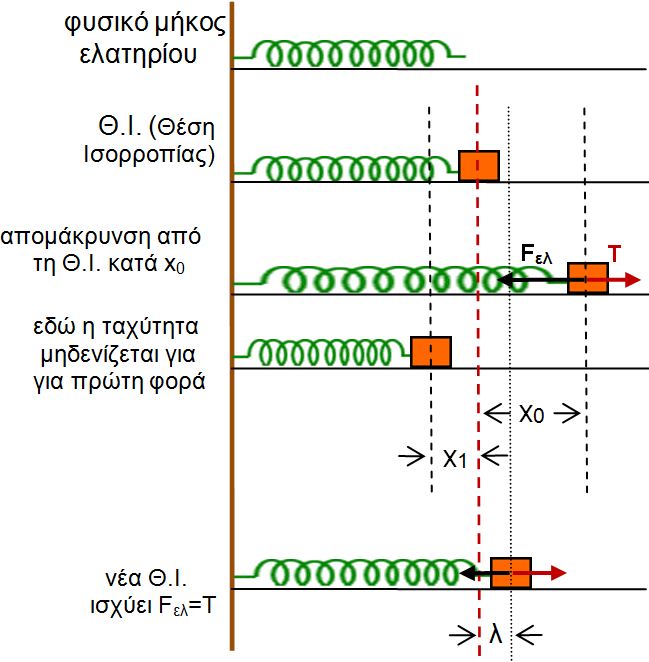Αποτέλεσμα εικόνας για οριζοντιο ελατηριο διαφορικη εξισωσηΟι δυνάμεις στον ταλαντωτη είναι η τάση Τ = -kx  (Η Δύναμη που ασκείται στο ελατήριο για να επιμηκυνθει κατά x είναι kx) 

 Η δύναμη επαναφοράς προσδίδει επιτάχυνση α F επ = mα.
H μετατόπιση είναι x 
H ταχύτητα στον ταλαντωτη είναι η πρώτη παράγωγος της μετατόπισης dx/dt =y (ταχύτητα)
Η επιτάχυνση στον αρμονική ταλαντωτή θεωρείται η δεύτερη παράγωγος της μετατόπισης ίση με α= d2x/dt2 
 
Η δύναμης επαναφοράς είναι ky ( k σταθερά του ελατηρίου)ενώ η  Γνωρίζουμε πως η επιτάχυνση είναι η δεύτερη παράγωγος του διαστήματος ως προς χρόνο. Άρα  F επ = md2x/dt2)
 
 F επ -Τ =0
md2x/dt2   - kx  =0

β. Εξίσωση Εκκρεμούς (αρμονικός τακαντωτής)

 

 

 

γ. Ηλεκτρικές ταλαντώσεις LC

Παράδειγμα το κύκλωμα RC 

Electrical SystemΚύκλωμα L C Ηλεκτρικές ταλαντώσεις

UL +Uc =0

αν q=y   x=t                 

Η Επαγωγική τάση που προκείται  UL = Εεπ =  -L.dI / dt.   = -Ld2q / dt 2      (dy/dx = dI / dt) Το ηλεκτρικό ρεύμα που διαρέει το κύκλωμα  είνα    I = dq / dt  

Hτάση στα άκρα του πυκνωτή είναι Uc = q/C

αντικαθιστώντας έχουμε q/C  -Ld2q / dt 2 =0  

 

2. 2ης τάξης τύπου y΄΄ +  p1y΄ + poy =0

Παράδειγμα 

Κύκλωμα R L C Ηλεκτρικές ταλαντώσεις

Electrical System

UR+UL +Uc =0

 

αν q=y   x=t                

-Η Επαγωγική τάση που προκείται Εεπ =  -L.dI / dt.  = IR + IRE

  dy/dx = .dI / dt

Το ηλεκτρικό ρεύμα που διαρέει το κύκλωμα  είνα    I = dq / dt   και 

-η Τάση στα άκρα της αντίστασης είναι UR = IR= dq / dt .R

Αντικαθιστώντας έχουμε    Εεπ = -  L. (d )(dq / dt)/ dt   --> -  L. (d 2q / dt2)

-H τάση στα άκρα του πυκνωτή είναι Uc = dq / dt .R

H ΔΕ γίνρται -  L. (d 2q / dt2)  + dq / dt .R  + dq / dt .R =0       (αy΄΄ + βy΄+γy =0)

 

Στο πρόβλημα, του αρμονικού ταλαντωτή με απόσβεση

Σύστημα μάζας- ελατηρίου ισχύει ο νόμος του Hooke και υπάρχει ένας γραμμικός όρος απόσβεσης. Η Δύναμη επαναφοράς του ελατηρίου είναι ανάλογη με την απομάκρυνση από την θέση ισορροπίας και η δύναμη απόσβεσης είναι ανάλογη της ταχύτητας της κίνησης dy/dx =y΄.

Fελ = -ky και Fαπόσβεσης = -αy΄

Η συνολική δύναμη είναι F = Fελ  + Fαπόσβεσης   --> ma =  -ky  -αy΄ όμως a =d2y/dt και y΄ =dy/dt και έχουμε την ΔΕ

md2y/dt2  -αdy/dt - ky =0

Στο πρόβλημα του αρμονικού ταλαντωτή καταλήγουμε στην διαφορική εξίσωση Στο πρόβλημα του αρμονικού ταλαντωτή καταλήγουμε στην διαφορική εξίσωση     αν  πρόκειται για συνάρτηση    της μετατόπισης  σε  σχέση με τον χρόνο     

H μετατόπιση είναι x 

-Η δύναμη στον ταλαντωτη είναι F= mα. 
Η επιτάχυνση στον αρμονική ταλαντωτή θεωρείται η δεύτερη παράγωγος της μετατόπισης ίση με α= d2x/dt2 όπου  F= m d2x/dt2
Η επιτάχυνση στον αρμονική ταλαντωτή θεωρείται επίσης  η πρώτη παράγωγος της ταχύτητας α= dy/dt  
-Η δύναμης επαναφοράς T είναι ky ( k σταθερά του ελατηρίου) T = -ky
-H ταχύτητα στον ταλαντωτη είναι η πρώτη παράγωγος της μετατόπισης dx/dt =y (ταχύτητα)
Η απόσβεση N λόγω τριβών ή άλλης εξωτερικής αιτίας, θεωρείται ανάλογη της ταχύτητας (b.dy/dx ) b σταθερά απόσβεσης  N=(b.dy/dx
Έτσι
               
      
m d2x/dt2= -b.dy/dx - kx        
 για m=1 έχουμε
dy/dt  = -b/m(dx/dt)- (k/m) x 
dy/dt  = = -b(dx/dt)- k x  
dy/dt  = -by- k x  
 
επειδή b2<< 4k  προσεγγοστικά
 
dy/dt = - [x(b(y/x)+ k )]/y
 
θέτουμε y/x =R(x)  οπ'οτε y=R(x)x
μετασχηματίζουμε
dy/dt = R + x (dR/dx)  και 
ολοκληρώνουμε
 και καταλήγουμε σε τελική λύση 
1/2 ln[y2/x2  +b.y/x +k] - b/2 . 1/(k-b24)1/2 tan-1 [(y/x + b/2 )/(k- b2/4)1/2] = -lnx + c

 

                                                                                   Î£Ï‡ÎµÏ„ική εικόνα

 

 2ης τάξης τύπου y΄΄ +  p1y΄ + poy = f(x)

Εξαρτημένη ταλάντωση

Κίνηση αρμονικού ταλαντωτή με απόσβεση που δέχεται εξωτερική διέγερση f(x)

αν   x=t   το  f(x) είναι  f(t)

δουλρ΄ύοντας ανάλογα έχουμε 

md2y/dt2  -αdy/dt - ky =f(t)

 
Πίσω