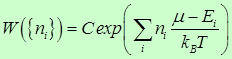Σε συστήματα που αποτελούνται από μικροσωματίδια
Κάθε επίπεδο ενέργειας χαρακτηρίζεται από μια συγκεκριμένη κατάσταση του συστήματος ή ένα υποσύνολο σε περίπτωση εκφυλισμού (όταν ένα φυσικό μέγεθος που χαρακτηρίζει ένα φυσικό κβαντικό σύστημα παίρνει την ίδια τιμή για διαφορετικές καταστάσεις )
Η ιδέα είναι εφαρμόσιμη σε άτομα (για τα επίπεδα ηλεκτρονίων, μόρια (δονητικά και περιστροφικά επίπεδα) ατομικούς πυρήνες (επίπεδα ενδομοριακής ενέργειας) κ.ο.κ,
Σε κβαντικές καταστάσεις διακρίνουμε την βασική κατάσταση στην οποία το σύστημα έχει την ελάχιστη ενέργεια ενώ όλες οι υπόλοιπες περιγράφονται σαν διεγερμένες (με ενέργεια υψηλότερη από τη βασική)
Παράδειγμα κβαντικών ενεργειακών καταστάσεων σε ένα σύστημα μπορούμε να πάρουμε το άτομο.
Η ενέργεια του ατόμου αλλάζει με άλματα σε ορισμένα τμήματα, διαφορετικά για διαφορετικά άτομα.
Δηλαδή παίρνει μόνο ορισμένες επιλεγμένες τιμές χαρακτηριστικές κάθε ατόμου.
Οι πιθανές τιμές της εσωτερικής ενέργειας ενός ατόμου ονομάζονται ενεργειακά ή κβαντικά επίπεδα
Επίπεδο ενέργειας - ΒικιπαίδειΠ
Θερμικό μήκος κύματος - Βικιπαίδεια
Για να περιγράψουμε πιο αναλυτικά τον διαχωρισμό πρέπει να έχουμε τα εξής:
Μήκος κύματος de Broglie
Θεωρείται σε σωματίδιο μάζας m και ταχύτητας u αντιστοιχεί μήκος κύματος ώστε mu=h/λ
Το θερμικό μήκος κύματος de Broglie
ή θερμικό μήκος κύματος de Broglie λth ή θερμικό μήκος κύματος Λ
Αυτό είναι περίπου το μισό μήκος κύματος de Broglie των σωματιδίων σε ένα ιδανικό αέριο
Είναι καθοριστικό για να κατατάξουμε τα σωματίδια σε κατηγορίες.
Εάν το Λ είναι πολύ μικρότερο από την απόσταση μεταξύ των σωματιδίων τότε πρόκειται για κλασσικό αέριο και ισχύει η κατανομή Boltzman Einstein
Εάν το Λ είναι μεγαλύτερο ή της τάξης της απόστασης μεταξύ των σωματιδίων τότε θα κυριαρχήσουν κβαντικά φαινόμενα και το αέριο θα πρέπει να θεωρhθεί ως αέριο Fermi ή αέριο Bose, oπότε ικανοποιεί είτε τις στατιστικές Fermi-Dirac ή τις τιστικές Bose Einstein
Τον όγκο που αντιστοιχεί σε κάθε σωματίδιο και την μέση απόσταση των σωματιδίων
Αν θεωρήσουμε V/Ν τον όγκο που αντιστοιχεί σε κάθε σωματίδιο (όπου V συνολικός όγκος του αερίου και Ν ο αριθμός των σωματιδίων) τότε η μέση απόσταση των σωματιδίων θα είναι η τρίτη ρίζα του όγκου αυτού, δηλαδή
Μέση απόσταση των σωματιδίων (V/Ν)1/3
Την βασική αρχή της στατιστικής φυσικής που ισχύει και στην κλασσική και στην κβαντική φυσική
Όταν Εi συστημα πανομοιότυπων φερμιονίων με ενέργειες στην κατάσταση ι (που υποδηλώνει το σύνολο των κβαντικών αριθμών μαζί και το σπιν)
διατυπώνεται ως εξής:
Η πιθανότητα ανίχνευσης ενός συστήματος που αποτελείται από πανομοιότυπα σωματίδια φερμιονίων με ενέργειες στην κατάσταση ι είναι
|
|
C σταθερά κανονικότητας, μ το χημικό δυναμικό. Ο αριθμός των σωματιδίων πρέπει να είναι σταθερός και ίσος με ![]()
Πότε ισχύουν οι στατιστικές Fermi- Dirac
Οι στατιστικές Fermy-Dirack ισχύουν σε σε χαμηλές θερμοκρασίες ή σε υψηλές συγκεντρώσεις και
για Λ<<<(V/N)1/3 ή V/NΛ3>>>1
Σε χαμηλές θερμοκρασίες οι ενέργειες των σωματιδίων είναι μεγάλες και το μήκος κύματος αυξάνεται και κυριαρχούν τα κβαντικά φαινόμενα
Οι στατιστικές Fermy-Dirack είναι κβαντικές στατιστικές που εφαρμόζονται σε συστήματα πανομοιότυπων φερμιονίων (σωματίδια με μισό ακέραιο σπιν που υπακούουν στην αρχή Pauli: μια κβαντική κατάσταση δεν μπορεί να καταληφθεί από περισσότερα από ένα σωματίδια). Καθορίζει την πιθανότητα με την οποία ένα δεδομένο ενεργειακό επίπεδο ενός συστήματος σε θερμοδυναμική ισορροπία καταλαμβάνεται από ένα φερμιόνιο.
Στις στατιστικές Fermi–Dirac, ο μέσος αριθμός σωματιδίων με ενέργεια
- ,
Πού είναι είναι η πολλαπλότητα του εκφυλισμού (ο αριθμός των καταστάσεων ενός σωματιδίου με ενέργεια ), - χημικό δυναμικό, είναι η σταθερά Boltzmann, – απόλυτη θερμοκρασία.
μεταφορά από
Στατιστικά στοιχεία Φέρμι-Ντιράκ - Βικιπαίδεια
Πότε ισχύουν οι στατιστικές Bose-Einstein
Στις στατιστικές Bose-Einstein σε χαμηλές θερμοκρασίες ή σε υψηλές συγκεντρώσεις σωματιδίων και
για Λ<<<(V/N)1/3 ή V/NΛ3>>>1
Είναι κβαντικές στατιστικές που εφαρμόζονται σε συστήματα πανομοιότυπων μποζονίων (σωματίδια με μηδενικό ή ακέραιο σπιν), όπως φωτόνια και άτομα ηλίου-4. Καθορίζει τον μέσο αριθμό μποζονίων σε κράτη με δεδομένη ενέργεια σε ένα σύστημα σε θερμοδυναμική ισορροπία:
- ,
Πού είναι είναι η πολλαπλότητα του εκφυλισμού (ο αριθμός των καταστάσεων ενός σωματιδίου με ενέργεια ), - χημικό δυναμικό, είναι η σταθερά Boltzmann, – απόλυτη θερμοκρασία. Αν , τότε η συνάρτηση του αριθμού των επιπέδων πλήρωσης σωματιδίων ονομάζεται συνάρτηση Bose-Einstein:
Στατιστικά στοιχεία Μπόουζ-Αϊνστάιν - Βικιπαίδεια
Οι στατιστικές Fermy-Dirack
Σε χαμηλές θερμοκρασίες οι ενέργειες των σωματιδίων είναι μεγάλες και το μήκος κύματος αυξάνεται και κυριαρχούν τα κβαντικά φαινόμενα
Οι στατιστικές Fermy-Dirack είναι κβαντικές στατιστικές που εφαρμόζονται σε συστήματα πανομοιότυπων φερμιονίων (σωματίδια με μισό ακέραιο σπιν που υπακούουν στην αρχή Pauli: μια κβαντική κατάσταση δεν μπορεί να καταληφθεί από περισσότερα από ένα σωματίδια). Καθορίζει την πιθανότητα με την οποία ένα δεδομένο ενεργειακό επίπεδο ενός συστήματος σε θερμοδυναμική ισορροπία καταλαμβάνεται από ένα φερμιόνιο.
Στις στατιστικές Fermi–Dirac, ο μέσος αριθμός σωματιδίων με ενέργεια
- ,
Πού είναι είναι η πολλαπλότητα του εκφυλισμού (ο αριθμός των καταστάσεων ενός σωματιδίου με ενέργεια ), - χημικό δυναμικό, είναι η σταθερά Boltzmann, – απόλυτη θερμοκρασία.
Στατιστικά στοιχεία Φέρμι-Ντιράκ - Βικιπαίδεια

Οι στατιστικές Bose-Einstein είναι κβαντικές στατιστικές που εφαρμόζονται σε συστήματα πανομοιότυπων μποζονίων (σωματίδια με μηδενικό ή ακέραιο σπιν), όπως φωτόνια και άτομα ηλίου-4. Καθορίζει τον μέσο αριθμό μποζονίων σε κράτη με δεδομένη ενέργεια σε ένα σύστημα σε θερμοδυναμική ισορροπία:
- ,
Πού είναι είναι η πολλαπλότητα του εκφυλισμού (ο αριθμός των καταστάσεων ενός σωματιδίου με ενέργεια ), - χημικό δυναμικό, είναι η σταθερά Boltzmann, – απόλυτη θερμοκρασία. Αν , τότε η συνάρτηση του αριθμού των επιπέδων πλήρωσης σωματιδίων ονομάζεται συνάρτηση Bose-Einstein:
Στατιστικά στοιχεία Μπόουζ-Αϊνστάιν - Βικιπαίδεια
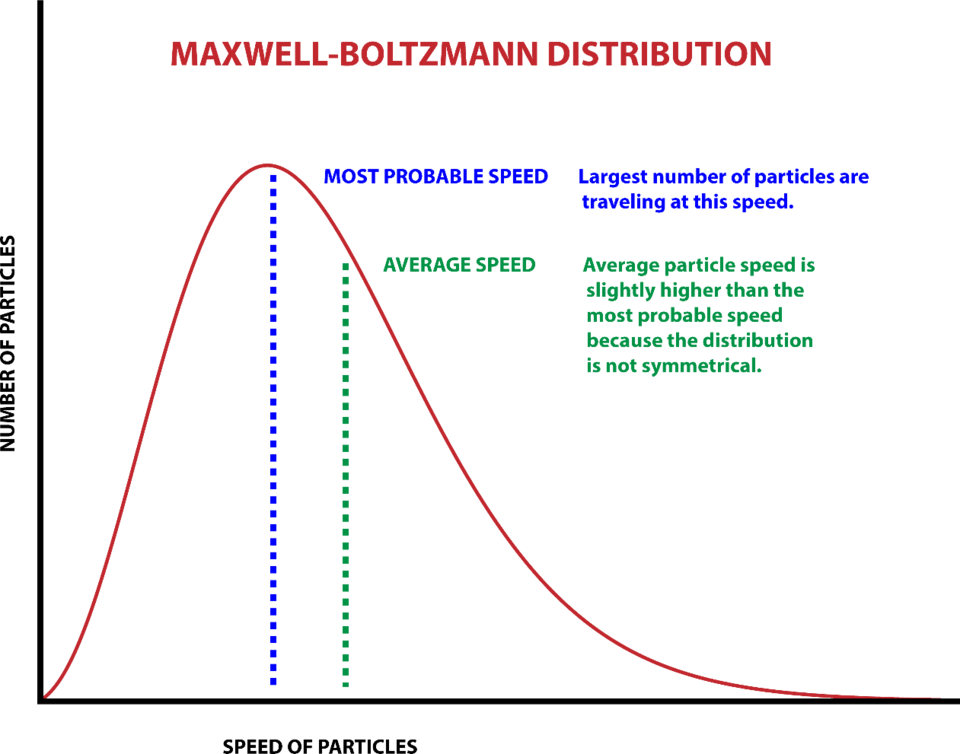
Σε υψηλές θερμοκρασίες ή/και χαμηλές συγκεντρώσεις σωματιδίων, οι στατιστικές Fermi-Dirac (καθώς και οι στατιστικές Bose-Einstein) περνούν στις στατιστικές Maxwell-Boltzmann.
για Λ<<<(V/N)1/3 ακολουθείται θεωρία Maxwell Boltzman
Δηλαδή, σε τέτοιες συνθήκες
Στατιστική μέθοδος για την περιγραφή φυσικών συστημάτων που περιέχουν μεγάλο αριθμό μη αλληλεπιδρώντων σωματιδίων που κινούνται σύμφωνα με τους νόμους της κλασσικής μηχανικής, Χρησιμοποιείται για τα κλασσικά ιδανικά αέρια
Δηλαδή, όταν η απόσταση μεταξύ των σωματιδίων είναι πολύ μεγαλύτερη από το θερμικό μήκος κύματος de Broglie, το αέριο θα υπακούει στις στατιστικές Maxwell-Boltzmann. Αυτό συμβαίνει με μοριακά ή ατομικά αέρια σε θερμοκρασία δωματίου, καθώς και με θερμικά νετρόνια που παράγονται από πηγή νετρονίων.

Στις στατιστικές Fermi–Dirac, ο μέσος αριθμός σωματιδίων με ενέργεια τρώω
- ,
Πού είναι είναι η πολλαπλότητα του εκφυλισμού (ο αριθμός των καταστάσεων ενός σωματιδίου με ενέργεια ), - χημικό δυναμικό, είναι η σταθερά Boltzmann, – απόλυτη θερμοκρασία.
Στατιστικά στοιχεία Φέρμι-Ντιράκ - Βικιπαίδεια