Δήμητρα Σπανού, χημικός, μόνιμη καθηγήτια Δ/θμιας Εκπ/σης στο 1ο Γυμνάσιο Δάφνης (μετά το 2010)
ΤΟ ΣΥΜΠΑΝΤΙΚΟ ΜΟΝΤΕΛΟ ΤΟΥ ΑΤΟΜΟΥ (Ernest Rutherford 1909)
Το μοντέλο για την δομή του ατόμου που πρότεινε ο Ernest Rutherford ήταν ότι υπάρχει στο άτομο μια κεντρική περιοχή που είναι συγκεντρωμένο όλο το θετικό φορτίο του (ο πυρήνας του) και γύρω από τον πυρήνα, σε κυκλικές τροχιές κινουνται τα αρνητικά ηλεκτρόνια ενώ ενδιάμεσα υπάρχει πολύς κενός χώρος. (πλανητικό μοντέλο)
Η εκδοχή ότι τα ηλεκτρόνια περιστρέφονται γύρω από τον πυρήνα διατυπώθηκε εφόσον έγινε αποδεκτή η έλξη του λόγω της ηλεκτρικής δύναμης Coulomb η οποία έπαιζε τον ρόλο της κεντρομόλου κινητήριας δύναμης των ηλεκτρονίων.
Το μειονονέκτημα αυτής της θεωρίας είναι πως,
η ελκτική αυτή δύναμη θα είχε αποτέλεσμα τα περιστρεφόμενα ηλεκτρόνια να πλησιάζουν συνεχώς προς τον πυρήνα ώστε το άτομο θα έπρεπε να συρρικνώνεται διαρκώς
Για να ξεπεραστούν αυτά τα μειονεκτήματα και να προχωρήσει η κατανόηση της δομής του ατόμου
είναι απαραίτητη η θεωρία της κβάντωσης των μεγεθών
Η αποδοχή της κβάντωσης (ποσοτικοποίησης) των φυσικών μεγεθών είναι απαραίτητη προϋπόθεση για να κατανοήσουμε την δομή των ατόμων.
Η ποσοτικοποίηση (κβάντωση) επιδιώκει τον ποσοτικό προσδιορισμό ενός μεγέθους με την χρήση μιας ποσοτικοτοποιημένης ποσότητας (κβάντου)
Με αυτήν επιτυγχάνεται η αναπαράσταση ιδιοτήτων σε μαθηματικά μετρήσιμες ποσότητες. Για τον λόγο αυτόν αναπτύσσονται μοντέλα (πρωτότυπα) για κάθε θεματική περιοχή. Παραδείγματα τέτοιων πρωτοτύπων από τις φυσικές επιστήμες μπορούν να είναι η ποσότητα ηλεκτρικού φορτίου το ηλεκτρικό φορτίο ενός ηλεκτρόνιου, ποσότητα μιας χημικής ουσίας το άτομο ή το μόριο, η διαβίβαση του νευρικού σήματος το ουδός
Η ΚΒΑΝΤΩΣΗ ΤΩΝ ΤΡΟΧΑΙΩΝ ΠΕΡΙΣΤΡΟΦΗΣ ΚΑΙ ΤΗΣ ΣΥΝΟΛΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΤΩΝ ΗΛΕΚΤΡΟΝΙΩΝ ΤΟΥ ΑΤΟΜΟΥ ( Νeilσ Bohr 1913)
Ο Neils Bohr το 1913 συμπλήρωσε αυτήν την θεωρία με την παραδοχή της ενεργειακής κβάντωσης των τροχαιών των ηλεκτρονίων. Η απόσταση από τον πυρήνα και η ενέργεια που μπορεί να έχει ένα ηλεκτρόνιο σε κάθε τροχαιάς περιστροφής του, είναι κβαντισμένη.
Αρχικά διατυπώνεται πως, η απόσταση r της τροχαιάς περιστροφής ηλεκτρονίου από τον πυρήνα είναι κβαντισμένη (ακτίνα της τροχαιάς), και καθορίζεται από την συνθήκη κβάντωσης της στροφορμής του ηλεκτρονίου L που πρέπeι να είναι ακέραιο πολλαπλάσιο της ποσότητας h/2π.
Δηλαδή L=mur= h/2π Αυτό αποτελεί την 1η συνθήκη του Bohr
Η 2η συνθήκη συνθήκη αφορά την κβάντωση της ενέργειά του. Η ολική ενέργεια του περιστρεφόμενου ηλεκτρονίου δίνεται από την σχέση
Εn= -2,18. 10-18/n2 όπου n= 1,2,3... ο κύριος κβαντικός αριθμός ο οποίος καθορίζει την ενεργειακή στάθμη του ηλεκτρονίου
Πριν προχωρήσουμε στην επόμενη 3η συνθήκη του Bohr χρειάζεται να σημειώσουμε ότι σύμφωνα με τον φυσικό νόμο της ελαχίστης ενέργειας τα άτομα βρίσκονται στην θεμελιώδη κατάσταση όταν τα ηλεκτρόνιά τους είναι σε θέσεις όσο το δυνατόν πλησιέστερα στον πυρήνα
O Bohr έδωσε την 2η κι 3η συνθήκηη που δεν αφορούν ακριβώς το θέμα μας, (που είναι η δομή του ατόμου) αλλά δίνουν μια εικόνα για την κβάντωση μεγεθών :
Η 3η συνθήκη του Bohr έχει σχέση με την αλλαγή της ενέργειας του ηλεκτρονίου πράγμα που μπορεί να συμβεί αν για εξωτερικούς λόγους, αυξηθεί ή ελλατωθεί η ενέργειά του. Αυτό γίνεται με την απορρόφηση (για αύξηση) ή την εκπομπή (για ελάττωση) ενέργειας με την μορφή ακτινοβολίας.
Όμως τα ποσά αυτής της ενέργεια στα ηλεκτρόνια δεν παίρνουν οποιεσδήποτε τιμές αλλά απορροφάτται και εκπέμπτεται ανά συγκεκριμένα ποσά (κβάντα ) και κάθε κβάντο μεταφέρει ενέργεια που δίνεται από την σχέση Ε= h.ν όπου h είναι η σταθερά του Plank ίση με 6,63. 10-34 js και είναι η διαφορά ενέργειας μεταξύ της αρχικής και της τελικής ηλεκτρονιακής στάθμης
Ο Neils Bohr αδυνατεί να περιγράψει τις μεγαλύτερες ηλεκτρονιακές στοιβάδες
Το πρότυπο του Bohr μπόρεσε να περιγράψει ικανοποιητικά, άτομα που διαθέτουν ένα μόνο ηλεκτρόνιο, όπως το άτομο του υδρογόνου και το κατιόν Ηλίου (He+). Δεν μπορεί να δώσει ικανοποιητική περιγραφή ατόμων με περισσότερα ηλεκτρόνια. Αυτό γίνεται πολύ καλύτερα στην συνέχεια με την καβαντική θεώρηση της δομής του ατόμου/
Μετά τον Ν. Bohr περνάμε σε μια εποχή που οι παλιές αρχές της Φυσικής αμφισβητούνται. Αμφισβητείται ακόμα και το αυτονόητο της ύπαρξης της υλης με την μαζική της μορφή και έρχεται μια νέα , τότε ιδέα, της κυματοειδούς φύσης των πάντων, ακόμα και της ύλης. Ταυτόχρονα, η θεωρία αυτή ενσωματώνει την κβάντωση των φαινομένων κι έτσι τα σωματίδια αντιμετοπίζονται πια σαν κυματικά πακέτα
Η εφαρμογή της θεωρίας αυτής στην ερμηνεία της δομής του ατόμου, εκφράζεται από την θεωρία και τις εξισώσεις του Ervin Schrodinger
Η ΥΠΌΘΕΣΗ ΤΟΥ DE BROGLIE (1923)
Tα κινούμενα σωματίδια μπορούν να θεωρηθούν σαν ένα ηλεκτρικό κύμα
.jpg)
Επιρεασμένος από την εμφάνιση και επικράτηση της θεωρίας της κυματομηχανικής, και αφού έγινε αποδεκτή η θεωρία φωτονίων του A. Einstein που θεωρούνται σωματίδια και κύμα, , ο de Broglie, διατυπώνει την αντίστροφη υπόθεση και βάσει αυτής, τα σωματίδια μπορούν να επιδείξουν ιδιότητες κυμάτων και πως ένα κινούμενο ηλεκτρόνιο στο άτομο μπορεί να θεωρηθεί και σαν ένα ηλεκτρικό κύμα . Το μήκος κύματος λαμβάνεται από την εξίσωση του Εinstein για την ορμή
λ=h/mv (h η σταθερά του Plank, m η μάζα, v η ταχύτητα κίνησης)
Η ΘΕΩΡΙΑ ΤΩΝ ΑΤΟΜΙΚΩΝ ΤΡΟΧΙΑΚΩΝ (Ε. Schrodinger 1927)
To ηλεκτρόνιο για τον E. Schrodinger δεν αποτελεί ένα σωματίδιο, αλλά, ένα ηλεκτρικά φορτισμένο νέφος.
Στην κυματοειδή εξίσωση του Schrodinger,
η κυματοσυνάρτηση Ψ είναι μια σύνθετη συνάρτηση που χρησιμοποιείται στην κβαντική μηχανική που αποδίδει την χωρική κατανομή του φορτίου του ηλεκτρονίου
Οι Εξισώσεις Schrödinger το 1927, είναι η Ψ και Ψ2
Η επίλυση της Ψ δίνει την πιθανότητα εύρεσης του ηλεκτρονίου ενός ατόμου, σε ορισμένο χώρο
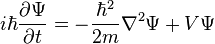
Σε κάθε χρονική στιγμή η εξίσωση δίνει τιμή σε κάθε σημείο του χώρου
Στο πρώτο μέρος παίρνουμε την αλλαγές στο σχήμα της Ψ με τον χρόνο
Σε κάθε σημείο του χώρου αποδίδονται στην κυματοσυνάρηση δύο αριθμοί
Στο δεύτερο μέρος ο πρώτος όρος (Λαπλασιανή) δίνει την περιγραφή της μεταβολής στον χώρο και ο δεύτερος όρος περιγράφει τις δυνάμεις που δρουν στο σωματίδιο
Οι εξισώσεις Schrodinger που βρίσκουν εφαρμογή σε σωματίδια των οποίων
α. ο αριθμός πρέπει να παραμένει σταθερός
β. Δεν πρέπει να κινούνται με πολύ υψηλές ταχύτητες
γ. Να είναι σωματίδια όχι φωτόνια
Συσχετίζουν την κυματική και σωματιδιακή συμπεριφορά και ανοίγουν τον δρόμο για την κβαντομηχανική
Με αυτές τις εξισώσεις, υπολογίζεται η Ενέργεια του ηλεκτρονίου ενός ατόμου, και η πιθανότητα εύρεσης του ηλεκτρονίου αυτού σε ορισμένο χώρο
Η συνάρτηση Ψ είναι μιγαδική και δεν μπορούμε να αποδώσουμε εύκολα σε αυτήν φυσική σημασία
έτσι εισάγεται από τον ίδιο μια δεύτερη συνάρτηση το τετράγωνο του μέτρου της Ψ ,
|Ψ(r, t)| 2 , που είναι πραγµατική συνάρτηση και εποµένως ϑα µπορούσε να δοθεί ϕυσική ερµηνεία σε αυτό.
Αυτή η φυσική ερμηνεία είναι η πυκνότητα της πιθανότητας να βρίσκεται το σωματίδιο τη χρονική στιγµή t στον όγκο dr = dxdydz στο σηµείο r
και είναι ανάλογη του |Ψ(r, t)| 2dr:
από
Η άποψη του Ε. Strondinger για την σωματιδιακή φύση των ηλεκτρονίων (και των σωματιδίων) αποκλείει την σωματιδιακή τους φύση
Η θεωρία της κυματοειδούς φύσης των ηλεκτρονίων από τον E. Strondinger έδωσε κι αυτή μειονεκτήματα. Πρώτο αυτό που ήδη αναφέρθηκε, σχετικά με την δυσκολία απόδοσης φυσικής σημασίας σε μια μιγαδική συνάρτηση που αναιρεί την σωματιδιακή των ηλεκτρονίων και τα θεωρεί σαν χωρική κατανομή του φορτίου του ηλεκτρονίου στον χώρο. Δεύτερο πολλά χαρακτηριστικά συμπεριφοράς των ηλεκτρονίων εξηγούνται μόνο εάν παραδεχτούμε την σωματιδιακή τους φύση
Η επόμενη προσπάθεια που γίνεται για την βελτίωση των θεωριών που προσπαθούν να ερμηνεύουσουν την δομή του ατόμου είναι από τον Max Bohn
Η ΣΤΑΤΙΣΤΙΚΗ ΕΡΜΗΝΕΙΑ ΤΗΣ ΚΥΜΑΤΟΣΥΝΑΡΤΗΣΗΣ ΑΠΟ ΤΟΝ MAX BORN 1926 (βραβειο Nobel 1954)
ΚΑΙ ΕΡΜΗΝΕΥΕΙ ΦΑΙΝΟΜΕΝΑ ΣΩΜΑΤΙΔΙΑΚΗΣ ΦΥΣΗΣ ΤΩΝ ΗΛΕΚΤΡΟΝΙΩΝ
Σe αντίθεση με τον Strondinger που θεώρησε το ηλεκτρόνιο σαν πακέτο κύματος, η στατιστική ο Born βασίζεται στην σωματιδιακή φύση του ηλεκτρονίου. Θεωρεί το ηλεκτρόνιο ως ένα αρνητικά φορτισμένο στοιχειώδες σωματίδιο. Όμως η κίνηση του ηλεκτρονίου δίνει μια λογική πιθανότηττας να βρίσκεται στα διάφορα σημεία του χώρου που κινείται. Αυτή η πιθανοτική ερμηνεία ακολουθεί την συνάρτηση κύματος του Strondinger και με αυτόν τον τρόπο φαίνεται να συμπληρώνει και όχι να αναιρεί την κυματοσυνάρτηση . Χάνεται η έννοια της τροχαιάς σαν κυματικό πεδίο αλλά εξετάζεται η πιθανότητα, να βρίσκεται το ηλεκτρόνιο σε ένα συγκεκριμένο σημείο του χώρου που περιβάλλει τον πυρήνα του ατόμου
Αργότερα το 1950 οι δύο θεωρείες έμοιαζαν να συγκλίνουν 
Δήμητρα Σπανού
ΠΗΓΕΣ
https://el.wikipedia.org/wiki/%CE%91%CF%84%CE%BF%CE%BC%CE%B9%CE%BA%CF%8C_%CF%80%CF%81%CF%8C%CF%84%CF%85%CF%80%CE%BF_%CF%84%CE%BF%CF%85_%CE%9C%CF%80%CE%BF%CF%81
PPT - Η δομή του ατόμου. PowerPoint Presentation, free download - ID:6379028 (slideserve.com)
Μαξ Μπορν - Βικιπαίδεια (wikipedia.org)
Στατιστική ερμηνεία της κυματοσυνάρτησης - Βικιπαίδεια (wikipedia.org)
Atomic Model Timeline by Pearson Ihmels | Timetoast timelines
ακατέργαστο
Ατομικό τροχιακό
Ατομικό τροχιακό ( τροχιακό ηλεκτρονίων ) - κυματική συνάρτηση ενός ηλεκτρονίου , που προκύπτει με την επίλυση της εξίσωσης Schrödinger για ένα δεδομένο άτομο [1] ; δίνεται από τον κύριο , τροχιακό και μαγνητική - κβαντικοί αριθμοί
Ένα σύνολο ατομικών τροχιακών με την ίδια τιμή του κύριου κβαντικού αριθμούαποτελεί ένα κέλυφος ηλεκτρονίων
Ένα άτομο κάθε χημικού στοιχείου έχει ένα πλήρες σύνολο όλων των τροχιακών.
, η πλήρωσή τους με ηλεκτρόνια συμβαίνει καθώς αυξάνεται ο σειριακός αριθμός, δηλαδή το φορτίο του πυρήνα και, κατά συνέπεια, ο αριθμός των ηλεκτρονίων.
Λειτουργία υπολογίζεται λύνοντας την εξίσωση Schrödinger στο πλαίσιο της προσέγγισης ενός ηλεκτρονίου ( μέθοδος Hartree-Fock ) ως η κυματική συνάρτηση ενός ηλεκτρονίου σε ένα αυτοσυνεπές πεδίο που δημιουργείται από τον ατομικό πυρήνα με όλα τα άλλα ηλεκτρόνια του ατόμου. Για απλοποίηση, ο υπολογισμός συχνά περιορίζεται στην εύρεση των ιδιοσυναρτήσεων της εξίσωσης Schrödinger για ένα ηλεκτρόνιο στο δυναμικό Coulomb .
ακατέργαστο
Το ατομικό τροχιακό είναι έννοια η οποία εισήχθη στις αρχές του 20ού αιώνα μέσω της κβαντικής θεωρίας και η οποία προσδιορίζει μια περιοχή του τρισδιάστατου χώρου στην οποία υπάρχει πιθανότητα να βρεθεί το ηλεκτρόνιο ενός ατόμου. Κάθε ηλεκτρόνιο ενός ατόμου βρίσκεται σε ένα ορισμένο τροχιακό.
Ένα ατομικό τροχιακό, στα κβαντομηχανικά μοντέλα ατόμων, είναι η χωρική κυματική συνάρτηση ενός μόνο ηλεκτρονίου σε κβαντομηχανική κατάσταση, κυρίως σε ακίνητη κατάσταση. Το σύμβολό του είναι κυρίως
(μικρό φι) ή
(μικρό psi). Το τετράγωνο του ποσού
περιγράφει τη χωρική κατανομή ως συνάρτηση πυκνότητας
Ο ίδιος ο E. Schrodinger θεωρούσε ένα ηλεκτρόνιο σε ένα άτομο ως αρνητικά φορτισμένο νέφος, η πυκνότητα του οποίου είναι ανάλογη με το τετράγωνο της τιμής της κυματικής συνάρτησης στο αντίστοιχο σημείο του ατόμου. Με αυτή τη μορφή, η έννοια του νέφους ηλεκτρονίων έγινε επίσης αντιληπτή στη θεωρητική χημεία. Η πιθανολογική ερμηνεία του τετραγώνου της κυματικής συνάρτησης τεκμηριώθηκε από τον M. Born ; Schrödinger στο άρθρο "Τι είναι ένα στοιχειώδες σωματίδιο;" (1950) συμφώνησε με τα επιχειρήματα του Born, ο οποίος τιμήθηκε με το Νόμπελ Φυσικής το 1954 με τη διατύπωση "Για θεμελιώδη έρευνα στον τομέα της κβαντικής μηχανικής, ειδικά για τη στατιστική ερμηνεία της κυματικής συνάρτησης ".
https://ru.wikipedia.org/wiki/%D0%90%D1%82%D0%BE%D0%BC%D0%BD%D0%B0%D1%8F_%D0%BE%D1%80%D0%B1%D0%B8%D1%82%D0%B0%D0%BB%D1%8C
ΠΗΓΕΣ
https://ru.wikipedia.org/wiki/%D0%90%D1%82%D0%BE%D0%BC%D0%BD%D0%B0%D1%8F_%D0%BE%D1%80%D0%B1%D0%B8%D1%82%D0%B0%D0%BB%D1%8C
Сатурн - шестая планета от Солнца - презентация онлайн (ppt-online.org)