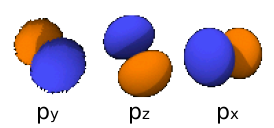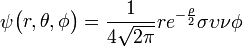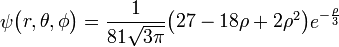Η ΧΗΜΕΙΑ ΠΕΡΙΓΡΑΦΕΙ ΤΗΝ ΥΛΗ ΜΕΣΑ ΑΠΟ ΤΗΝ ΣΥΓΧΡΟΝΗ ΦΥΣΙΚΗ: Δόμηση των ατόμων 3. Κατανομή των ηλεκτρονίων των ατόμων σε ηλεκτρονιακές στοιβάδες. Ατομικά τροχιακά. Μοριακά τροχιακά

Η ΧΗΜΕΙΑ ΠΕΡΙΓΡΑΦΕΙ ΤΗΝ ΥΛΗ ΜΕΣΑ ΑΠΟ ΤΗΝ ΣΥΓΧΡΟΝΗ ΦΥΣΙΚΗ: Δόμηση των ατόμων 3. Κατανομή των ηλεκτρονίων των ατόμων σε ηλεκτρονιακές στοιβάδες. Ατομικά τροχιακά. Μοριακά τροχιακά

Δήμητρα Σπανού, χημικός, μόνιμη καθηγήτρια στο 1ο Γυμνάσιο Δάφνης από το 2010

 

 

 

ΤΑ ΑΤΟΜΙΚΑ ΤΡΟΧΙΑΚΑ

Οι θεωρία της κυματοειδούς φύσης των ηλεκτρονίων του  Schrodinger που δίνουν την χωρική κατανομή του φορτίου του ηλεκτρονίου που θεωρείται σαν ηλεκτρικό κύμα,

 αλλά και η στατιστκή ερμηνεία του Max Born που δίνει την πιθανότητα να βρίσκεται το ηλεκτρόνιο - σωματίδιο σε διάφορα σημεία του χώρου στον οποίο  κινείται, 

δίνουν μια νέα εικόνα για την δομή του ατόμου αυτήν των ατομικών τροχιακών

Η θεωρία  των ατομικών και μοριακών τροχιακών πρότεινε     Robert Sanderson Mulliken, το 1932

 Η λύση της εξίσωσης Σρέντινγκερ δίνει ένα σύνολο κυματοσυναρτήσεων καθεμιά από τις οποίες αντιστοιχεί σε συγκεκριμένη τιμή ενέργειας του ηλεκτρονίου και αποτελεί το τροχιακό

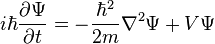
Όταν ορίσουμε την ενέργεια του ηλεκτρονίου Εn, 

 η  επίλυση της εξίσωσης Schrödinger οδηγεί στις κυματοσυναρτήσεις ψ που περιγράφουν την κατάσταση του ατομικού τροχιακού.

ΟΙ ΚΒΑΝΤΙΚΟΙ ΑΡΙΘΜΟΙ

Για να γίνει αυτό λαμβάνουμε υπ' όψην μας ότι κάθε ένα από τα ηλεκτρόνια του ατόμου είναι διαφορετικά ορισμένο από τους 4 κβαντικούς αριθμούς και τοποθετείται σε συγκεκριμένης απόσταση από τον πυρήνα που καθορίζεται από την ενέργειά τους και περιγράφεται με αυτούς τους κβαντικούς αριθμούς 

Κύριος κβαντικός αριθμός n (1,2,3,4,5,6,7) που προσδιορίζει απόσταση από τον πυρήνα   απόσταση από τον πυρήνα του ηλεκτρονίου και ταυτόχρονα της ενέργειας σε ακίνητη κατάσταση  Είναι (K/n=1, L/n=2, M/n=3, N/n=4, O/n=5, Q/n=6,

Τον Δευτερεύοντα κβαντικό αριθμο l  που προσδιορίζει τις υποστοιβάδες που περιλαμβάνει υποομάδες ηλεκτρονίων (υποστοιβάδες) της κάθε στοιβάδας ανάλογα με τον χώρο κατανομής τους . Δίνει το σχήμα του ηλεκτρονιακού νέφους 

 Παίρνει τιμές  l= 0, 1, 2 ,3, 4,   (n-1) . Οι υποστοιβάδες είναι οι s, p, d, f, g,h,i

Ηλεκτρόνια με ίδιο n και l βρίσκονται στην ίδια υποστοιβάδα

Ο μαγνητικός κβαντικός αριθμός ml καθορίζει τον προσανατολισμό του ηλεκτρονιακού νέφους σε σχέση με τους άξονες x, y, z, 

 δηλαδή, τα επίπεδα που θα κινηθεί το κάθε περιστρεφόμενο ηλεκτρόνιο

 Σε κάθε υποστοιβάδα που εμφανίζει λόγω αυτής της περιστροφής του μαγνητική ροπή και μηχανική ροπή λόγω αυτής, που  καθορίζεται από τον μαγνητικό αριθμό ml .

 Τιμές του μαγνητικού κβαντικού αριθμού αντιστοιχεί στο τροχιακά l. και είναι: -l, ...0...+l

Ο κβαντικός αριθμός ms  καθορίζεται από το άθροισμα των διανυσμάτων l και s δηλαδή περιλαμβάνει

την γωνιακή ορμή του ηλεκτρονίου που προκαλείται από την ιδιοπεριστροφή του (ορμή spin). Παίρνει τιμές 1/2 για στροφορμή παράλληλη με το Β του πεδίο και -1/2 για στροφορμή αντιπαράλληλη με το Β του πεδίου

Ηλεκτρόνια με ίδιο n, l, ml βρίσκονται στο ίδιο τροχιακό

dimitra-spanoy.cms.webnode.gr/scholika-mathimata-mia-synoptiki-kai-oso-ginetai-apli-paroysiasi-scholikon-mathimaton-tonizontas-kapoies-simantikes-gnoseis-poy-prepei-na-afomoiothoyn/chimeia-omadas-prosanatolismoy-thetikon-spoydon-kef1-apo-kanona-hund-kai-periodiko-pinaka-e/

 

ΟΙ ΑΡΧΕΣ ΤΗΣ ΔΟΜΗΣΗΣ ΕΝΟΣ ΠΟΛΥΗΛΕΚΤΡΟΝΙΑΚΟΥ ΑΤΟΜΟΥ

  • Σε ένα άτομο που έχει πολλά ηλεκτρόνια, η τοποθέτησή τους ακολουθεί ορισμένους κανόνες: 
  •  
  • Κάθε ηλεκτρόνιο του ατόμου είναι εντελώς καθορισμένο 

και πρέπει ένας τουλάχιστον από τους 4 κβαντικούς αριθμούς του να είναι διαφορετικός

  • Ο αριθμός των ηλεκτρονίων στους φλοιούς (στοιβάδες) πρέπει να είναι από ένα έως 2n2.   
  • Αν σε έναν εξωτερικό φλοιό (κέλυφος) ο αριθμός των ηλεκτρονίων φτάσει την οριακή τιμή το κέλυφος γεμίζει και αρχίζει να σχηματίζεται ένα νέο κέλυφος. 
  • Κάθε ένα από τα ατομικά τροχιακά  της κάθε  στοιβάδων συμπληρώνεται ανάλογα: με 2 ηλεκτρόνια (s υποστοιβάδα) 6 ηλεκτρόνια (p υποστοιβάδα), 10 ηλεκτρόνια (d υποστοιβάδα), κ.λ.π Τα ατομικά τροχιακά μιας υποστοιβάδας έχουν ίδιο κύριο και δευτερεύοντα κβαντικό αριθμό 

 

 

Η υποστοιβάδα s διαθέτει ένα μόνο επίπεδο περιστροφής και συμπληρώνεται με δύο ηλεκτρόνια.

Η υποστοιβάδα p διαθέτει τρία   επίπεδα περιστροφής τα x, y, z  και συμπληρώνεται με 2x3=6 ηλεκτρόνια.

Η υποστοιβάδα d διαθέτει πέντε    επίπεδα περιστροφής  και συμπληρώνεται με 2x5=10 ηλεκτρόνια.

 

ΑΠΟ ΤΗΝ ΕΠΙΛΥΣΗ ΤΗΣ ΕΞΙΣΩΣΗΣ SCHRODINGER

τα στοιχεία αυτά εισάγονται στην εξίσωση Schrodinger που μεταφέρω από

Η Ιστορία των Φυσικών Επιστημών. Μέρος Έβδομο: Πέρα από την Κλασσική Φυσική ΙΙ. Η Κβάντωση των Φυσικών μεγεθών: Η Ερμηνεία των κβαντικών φαινομένων από "σκληρά" Μαθηματικά

 

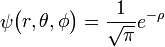\psi \begin{pmatrix} r, \theta, \phi \end{pmatrix} = \frac{1}{\sqrt{\pi}}e^{-\rho} , όπου \rho = \frac{r}{\alpha_0}, με \alpha_0 = \frac{h^2 \epsilon_0}{\pi m_e {q_e}^2}  « ακτίνα Bohr ». 

 

1s:AtomicOrbital n1 l0.png

 

 
 

2s:  \psi \begin{pmatrix} r, \theta, \phi \end{pmatrix} = \frac{1}{4 \sqrt{2 \pi}} \begin{pmatrix} 2 - \rho \end{pmatrix} e^{- \frac{\rho}{2}} . AtomicOrbital n2 l0.png

 
2px: n=2, \ell=1: \psi \begin{pmatrix} r, \theta, \phi \end{pmatrix} = \frac{1}{4 \sqrt{2 \pi}} re^{- \frac{\rho}{2}} \eta \mu \theta \sigma \upsilon \nu \phi .
2py: n=2, \ell=1: \psi \begin{pmatrix} r, \theta, \phi \end{pmatrix} = \frac{1}{4 \sqrt{2 \pi}} re^{- \frac{\rho}{2}} \eta \mu \theta \eta \mu \phi .              AtomicOrbital n2 l1.png
2pz: n=2, \ell=1: \psi \begin{pmatrix} r, \theta, \phi \end{pmatrix} = \frac{1}{4 \sqrt{2 \pi}} re^{- \frac{\rho}{2}} \sigma \upsilon \nu \phi
 
 
 
.
3s: n=3, \ell=0:  \psi \begin{pmatrix} r, \theta, \phi \end{pmatrix} = \frac{1}{81 \sqrt{3 \pi}} \begin{pmatrix} 27 - 18 \rho + 2 \rho^2 \end{pmatrix} e^{- \frac{\rho}{3}} AtomicOrbital n3 l0.png

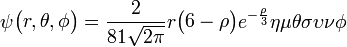3px: n=3, \ell=1: \psi \begin{pmatrix} r, \theta, \phi \end{pmatrix} = \frac{2}{81 \sqrt{2 \pi}} r \begin{pmatrix} 6 - \rho \end{pmatrix} e^{- \frac{\rho}{3}} \eta \mu \theta \sigma \upsilon \nu \phi .
3py: n=3, \ell=1: \psi \begin{pmatrix} r, \theta, \phi \end{pmatrix} = \frac{2}{81 \sqrt{2 \pi}} r \begin{pmatrix} 6 - \rho \end{pmatrix} e^{- \frac{\rho}{3}} \eta \mu \theta \eta \mu \phi .
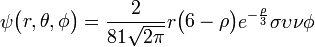
3pz: n=3, \ell=1: \psi \begin{pmatrix} r, \theta, \phi \end{pmatrix} = \frac{2}{81 \sqrt{2 \pi}} r \begin{pmatrix} 6 - \rho \end{pmatrix} e^{- \frac{\rho}{3}} \sigma \upsilon \nu \phi
 
     Αυτά είναι λοιπόν τα ατομικά τροχιακά ή αλλιώς οι τροχαιές όπως τις συνέλαβε αρχικά ο Bohr που δεν είναι βέβαια κυκλικές όμως είναι κοντά στην ιδέα που είχαν τότε. Βέβαια  εφ όσον τα τροχιακά προκύπτουν από πιο πολύπλοκες εξισώσεις, δεν έχουν το σχήμα που πρότειναν τότε το 1913, όμως η ιδέα τους ήταν γενικά σωστή ώστε τελειοποιήθηκε αργό τερα     
 
ΤΑ ΜΟΡΙΑΚΑ ΤΡΟΧΙΑΚΑ                                                                                                      

ΑΠΟ ΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ  ΑΤΟΜΙΚΩΝ ΤΡΟΧΙΑΚΩΝ  ΣΕ ΣΥΝΑΡΤΗΣΕΙΣ  ΜΟΡΙΑΚΩΝ ΤΡΟΧΙΑΚΩΝ

Οι όροι ατομικό τροχιακό και μοριακό τροχιακό εισήχθησαν από τον Robert S Mulliken to 1932

Όταν δύο ή περισσότερα άτομα συνδυάζονται χημικά για να σχηματίσουν μόριο, τα μοριακά τροχιακά συνδυάζονται επίσης ώστε να σχηματίσουν μοριακά τροχιακά και οι θέσεις των ηλεκτρονίων στα άτομα επίσης.

Αν θεωρήσουμε τα ατομικά  τροχιακά σαν μαθηματικές συναρτήσεις, τα μοριακά τροχιακά είναι επίσης μαθηματικές συναρτήσεις που προκύπτουν, με τον συνδυασμό των συναρτήσεων  που περιγράφουν ατομικά τροχιακά. 

Περιγράφουν την μαθηματική συμπεριφορά των ηλεκτρονίων στα μόρια

Οι γραμμικοί συνδυασμοί ατομικών τροχιακών ή τα αθροίσματα ή οι διαφορές τους παρέχουν λύσεις στις εξισώσεις  Hartee- Fock που αντιστοιχούν στην προσέγγιση ανεξάρτητων σωματιδίων της μοριακής εξίσωσης  Schrondinger.

Οι συνδυασμοί αυτοί  LCAO μπορούν να χρησιμοποιηθούν για τον υπολογισμό μοριακών τροχιακών που σχηματίζονται κατά την δημιουργία δεσμού μεταξύ ατόμων για την δημιουργία μορίων

 Για απλά διατομικά μόρια οι εξισώσεις διατυπώνονται μαθηματικά :

       

ca, cb    συντελεστές ψa και ψb  ατομικές κυματοσυναρτήσεις

 

Μοριακό τροχιακό - Βικιπαίδεια

ΚΑΤΑΣΚΕΥΗ ΜΟΡΙΑΚΩΝ ΤΡΟΧΙΑΚΩΝ

Η κατασκευή των μοριακών τροχιακών από ατομικά βασίζεται στην αρχή της υπέρθεσης που είναι ο συνδυασμος ατομικών τροχιακών για την δημιουργία μοριακών. Όταν τα άτομα ενώνονται, τα ατομικά τροχιακά επικαλύπτονται και αυτό δημιουργεί νέα μοριακά που ονομάζονται τροχιακά δεσμών ή δεσμικά τροχιακά

Τα μοριακά τροχιακά επιτρέπονται εάν οι συμμετρίες μεταξύ των ατομικών τροχιακών είναι συμβατές μεταξύ τους, δηλαδή εάν υπάρχει αλληλοεπικάλυψη των ατομικών τροχιακών γιατί αυτό δείχνει πόσο αλληλοεπιδρούν τα ατομικά τροχιακά μεταξύ τους κυρίως εκείνα που είναι παραπλήσια ενεργειακά 

 

ΔΕΣΜΙΚΑ , ΑΝΤΙΔΕΣΜΙΚΑ ΚΑΙ ΜΗ ΔΕΣΜΙΚΑ ΜΟΡΙΑΚΑ ΤΡΟΧΙΑΚΑ 

 Από η ατομικά τροχιακά που υπάρχουν αρχικά προκύπτουν η μοριακά τροχιακά. Από αυτά όμως δεν είναι όλα το ίδιο ευνοϊκα. 

Έτσι, έχουμε 3 είδη αλληλοεπικάλυψης ατομικών τροχιακών από τις οποίες προκύπτουν ανάλογα μοριακά τροχιακά: 

Τα δεσμικά (σχηματίζουν αυθόρμητους χημικούς δεσμούς) τα αντιδεσμικά και τα μη δεσμικά  

Τα δεσμικά μοριακά τροχιακά έχουν χαμηλότερη ενέργεια από εκείναι των αντίστοιχων ατομικών τροχιακών κι έτσι σταθεροποιούν τους χημικούς δεσμούς.

Τα αντιδεσμικά μοριακά τροχιακά που  έχουν υψηλότερη ενέργεια από εκείναι των αντίστοιχων ατομικών τροχιακών κι έτσι αποσταθεροποιούν τους χημικούς δεσμούς.

 

Τα μη δεσμικά μοριακά τροχιακά όπου,   έχουν ίση ενέργεια από εκείναι των αντίστοιχων ατομικών τροχιακών που τα σχημάτισαν.

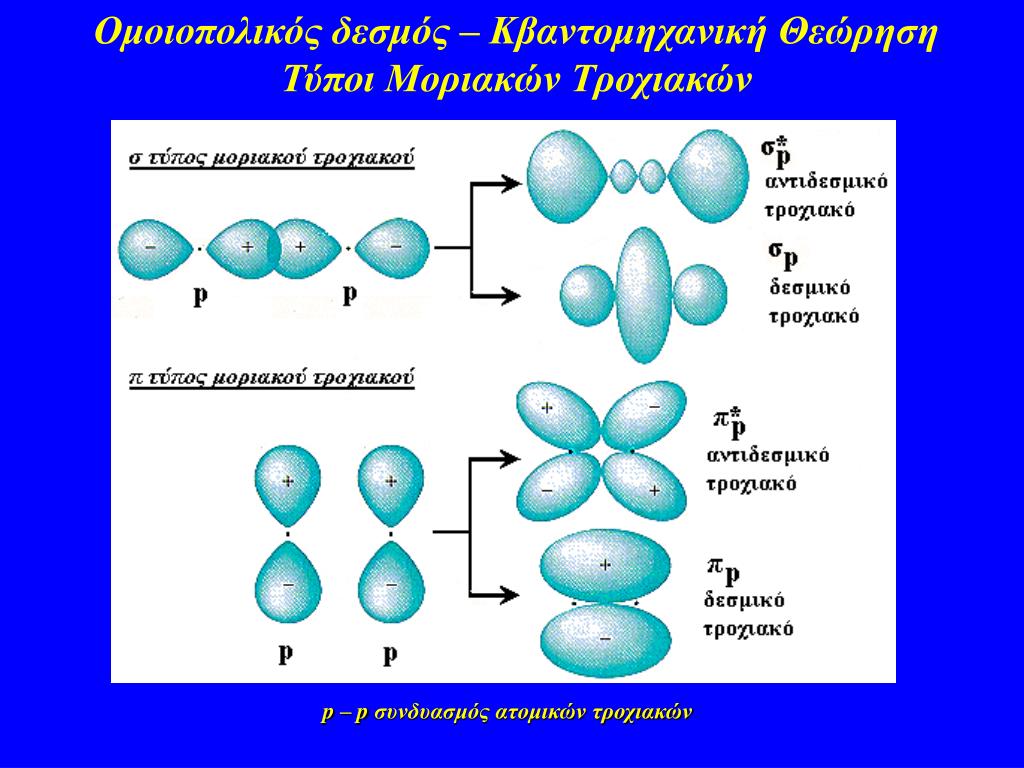
PPT - Υβριδισμός Ατομικών Τροχιακών ( Hybridization) PowerPoint ...

Ένα μόριο είναι σταθερό αν ο αριθμός των ηλεκτρονίων που βρίσκονται σε  δεσμικά μοριακά τροχιακά είναι μεγαλύτερος από  αυτά που βρίσκονται  σε μη δεσμικά μοριακά τροχιακά. Στα δεσμικά μοριακά τροχιακά ενός χημικού δεσμού, τα ηλεκτρόνια περνούν τον περισσότερο χρόνο ανάμεσα στους πυρήνες των ατόμων διευκολύνοντας τον δεσμό τους σε αντίθεση με τα αντιδιαμετρικά. 

Η φύση της κατανομής των ηλεκτρονίων σε μοριακό τροχιακό, καθορίζει την φύση του δεσμού, την ενέργειά του, τις διαπυρηνικές αποστάσεις, , τις μαγνητικές ιδιότητές του κ.α.

Η πολλαπλότητα των δεσμών σε ένα μόριο καθορίζεται από τη σχέση  Ν= (ηδεσμικά - η αντιδεσμικά )/2

ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΤΩΝ ΤΡΟΧΙΑΚΩΝ ΩΣ ΠΡΟΣ ΤΟΝ ΑΞΟΝΑ ΤΟΥ ΔΕΣΜΟΥ

ΣΥΜΜΕΤΡΙΚΑ ΚΑΙ ΑΝΤΙΣΥΜΜΕΤΡΙΚΑ ΔΕΣΜΙΚΑ ΤΡΟΧΙΑΚΑ 

Σε αντίθεση με τα ατομικά τροχιακά που είναι μονοκεντρικά, τα μοριακά τροχιακά είναι πολυκεντρικά. Τα μοριακά τροχιακά σχηματίζονται με συνδυασμό ατομικών τροχιακών  όταν αυτά  έρχονται αρκκκκκκετά κοντά 

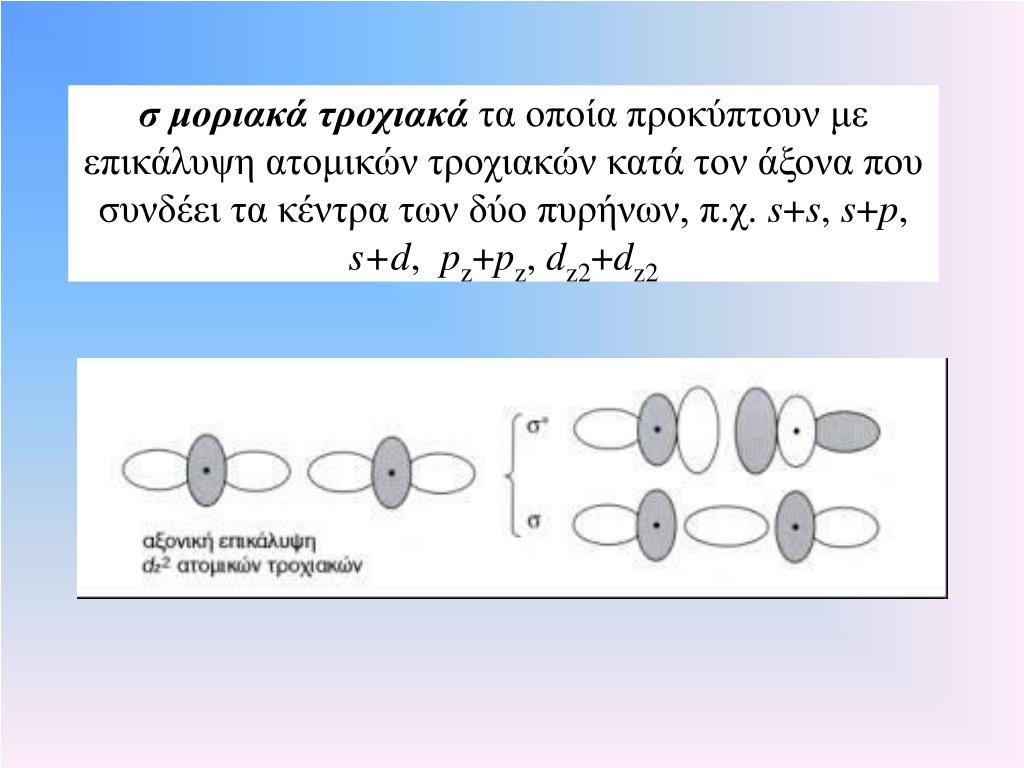
PPT - Σε ποια θεμελιώδη σημεία διαφέρει η θεωρία των μοριακών τροχιακών ...

PPT - Σε ποια θεμελιώδη σημεία διαφέρει η θεωρία των μοριακών τροχιακών ...

Τα μοριακά δεσμικά τροχιακά μπορεί να είναι συμμετρικά ή αντισυμμετρικά σε σχέση με το επίπεδο του μορίου. Τα μοριακά τροχιακά που ονομάζονται σίγμα (σ) προκύπτουν με επικάλυψη ατομικών τροχιακών κατά τον άξονα που συνδέει τα κέντρα των δύο πυρήνων των ατόμων που δημιουργούν χημικό δεσμο. Μπορει να είναι από δύο υποστοιβάδες s, ή από μια  s και μια dx υποστοιβάδα  κ.ο.κ.

Τα μοριακά τροχιακά που ονομάζονται π είναι  αυτά που η αλληλοεπικάλυψη των ατομικών τροχιακών για την δημιουργία του μοριακού, γίνεται σε κατεύθυνση κάθετη στον άξονα που συνδέει τα κέντρα των δύο πυρήνων των ατόμων που δημιουργούν χημικό δεσμο. Μπορει να είναι από δύο υποστοιβάδες η μια  s και μια dψ υποστοιβάδα  ήηηηηη  η μια  dψ με μια άλλη  dψ υποστοιβάδα από το δεύτερο 'ατομο κ.ο.κ.

 

ΓΡΑΜΜΙΚΟΙ ΣΥΝΔΥΑΣΜΟΙ ΑΤΟΜΙΚΩΝ ΤΡΟΧΙΑΚΩΝ ΑΠΟ ΟΠΟΥ ΠΡΟΚΥΠΤΟΥΝ ΟΙ ΜΟΡΙΑΚΑ ΤΡΟΧΙΑΚΑ

Όταν δύο ή περισσότερα άτομα συνδυάζονται χημικά σε μόριο οι θέσεις των ηλεκτρονίων καθορίζονται ώστε τα ατομικά τροχιακά να συνδυάζονται και να δημιουργούν μοριακά τροχιακά και τα ηλεκτρόνια κάθε ατόμου

PPT - Σε ποια θεμελιώδη σημεία διαφέρει η θεωρία των μοριακών τροχιακών ...

 καταλαμβάνουν μοριακά τροχιακά.

Με συνδυασμό δύο ίδιων ατομικών τροχιακών 

Τα μοριακά τροχιακά προσδιορίζονται με την μέθοδο LCAO  με τη μέθοδο αυτή μπορούμε να συνδυάσουμε ατομικά τροχιακά με ίδιες ή διαφορετικές ενέργειες και συμμετρίες και περιγράφουν καλύτερα την συμπεριφορά των ηλεκτρονίων στα μόρια.

Μοριακά τροχιακά , εκτός από τον συνδυασμό ατομικών τροχιακών, μπορούν να προκύψουν και από υβριδικά τροχιακά ή από συνδυασμό άλλων μοριακών τροχιακών. 

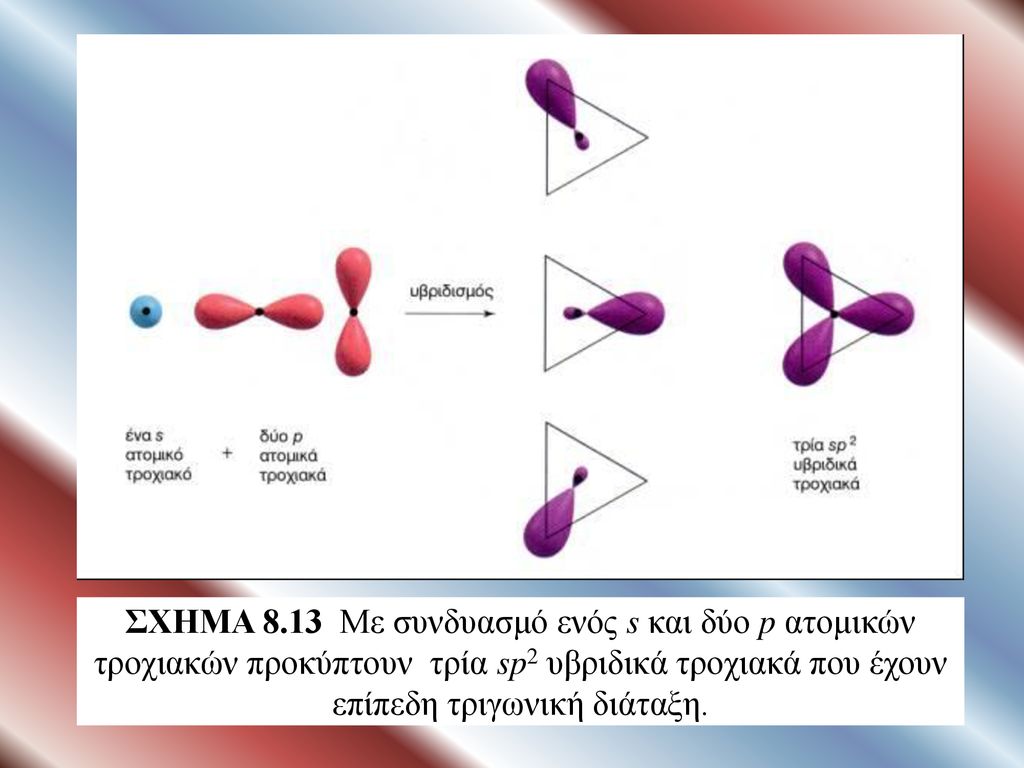ΤΑ ΒΑΣΙΚΑ ΣΗΜΕΙΑ ΣΤΗ ΘΕΩΡΙΑ ΔΕΣΜΟΥ ΣΘΕΝΟΥΣ - ppt κατέβασμαΤα υβριδικά τροχιακά του ίδιου ατόμου, είναι τροχιακά που προκύπτουν από την μίξη ατομικών τροχιακών του ατόμου αυτού που έχουν ίδια ενέργεια  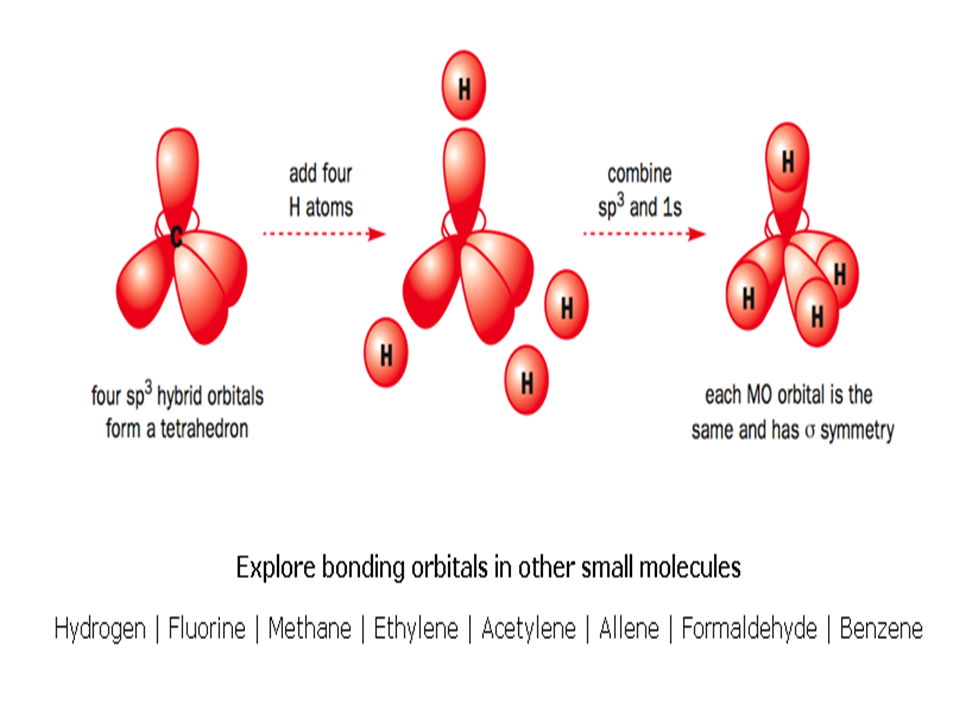Ο ΦΑΝΤΑΣΤΙΚΟΣ ΚΟΣΜΟΣ ΤΗΣ ΧΗΜΕΙΑΣ: Είδη του υβριδισμούκαι  που αυτό οδηγεί στην δημιουργία νέων ισότιμων τροχιακών που ονομάζονται υβριδικά τροχιακά και είναι ίσα σε αριθμό με τα ατομικά που συγχωνεύονται, όμως η συνολική ενέργεια των υβριδικών  τροχιαών είναι χαμηλότερη  από το άθροισμα των ενεργειών των ατομικών .

 

 Υβριδικά τροχιακά μπορεί να ενωθούν μεταξύ τους ή με άλλα ατομικά τροχιακά. 

Στο μεθάνιο CH4  έχουμε

α.  4 ισοδύναμα υβριδικά τροχιακά sp3 στον άνθρακα που κάνουν 4 σ μοριακούς δεσμούς με τα 4 άτομα υδρογόνου που έχουν από ένα ατομικό τροχιακό

Στο αιθένιο C2H4 έχουμε

β.  3 υβριδικά τροχιακά sp2 στον άνθρακα που κάνουν 3 σ μοριακούς δεσμούς, τους 2 με τα 2 άτομα υδρογόνου και 1 μεταξύ των υβριδοποιημένων τροχιακών των ανθράκων 

και 1 μοριακό τροχιακό μεταξύ των υβδιδοποιημένων τροχιακών των 2 ατόμων άνθρακα που σχηματίζουν ένα π μοριακό τροχιακό του διπλού δεσμού στον άξονα z

 

γ. Στο αιθίνιο C2H2 έχουμε

β.  2  υβριδικά τροχιακά sp2 στον άνθρακα που κάνουν συνολικά 2σ δεσμούς: 1 σ μοριακούς δεσμούς με τα 1 άτομο υδρογόνου (που έχουν από ένα ατομικό τροχιακό)  

και 1σ δεσμό  μεταξύ των υβδιδοποιημένων τροχιακών των 2 ατόμων άνθρακα

ακόμα  που σχηματίζουν 2 π ισότιμα  μοριακά τροχιακά του τριπλού δεσμού στον άξονα z και ένα στον y

 

 

               

Δήμητρα Σπανού

 

 

ΠΗΓΕΣ

https://infotables.ru/khimiya/825-elektronnye-formuly-atomov-khimicheskikh-elementov

Ατομικά τροχιακά και κβαντικοί αριθμοί – Η ηλεκτρονική τάξη Χημείας (sch.gr)

6.1 Τροχιακό-κβαντικοί αριθμοί (ebooks.edu.gr)

https://infotables.ru/khimiya/825-elektronnye-formuly-atomov-khimicheskikh-elementov

Ηλεκτρονική δομή - Βικιπαίδεια (wikipedia.org)

6.1 Τροχιακό-κβαντικοί αριθμοί (ebooks.edu.gr)

https://el.wikipedia.org/wiki/%CE%9C%CE%BF%CF%81%CE%B9%CE%B1%CE%BA%CF%8C_%CF%84%CF%81%CE%BF%CF%87%CE%B9%CE%B1%CE%BA%CF%8C

https://www.slideserve.com/koen/se-pa-e-ed-s-ea-dafe-ea-t-a-ta-ap-t-ea-des-s-vb

https://www.slideserve.com/koen/se-pa-e-ed-s-ea-dafe-ea-t-a-ta-ap-t-ea-des-s-vb

https://docplayer.gr/45953129-5-organometallikes-enoseis-ton-mm.html

https://www.slideserve.com/rufin/3271136#google_vignette

https://slideplayer.gr/slide/17116331/

 

 

ήλιον μαγνητική ροπή -2,12

Το ήλιο χρησιμοποιείται στην κρυογενική (είναι η μεγαλύτερη χρήση του, που καταναλώνει περίπου το ¼ της παραγωγής του) και στην ψύξη μαγνητών υπεραγωγιμότητας, με ειδικότερη εμπορική εφαρμογή τούς σαρωτές MRI.

 

Τα ηλεκτρόνια στο άτομο τοποθετούνται σε τροχαιές βάσει της ενέργειάς τους με σειρά από τις τροχαιές μικρότερης ενέργειας προς τις τροχαιές μεγαλύτερης ενέργειας.

Δεδομένου ότι, κάθε τροχαιά του ατόμου  συμπληρώνεται με δύο ηλεκτρόνια που κινούνται σε αντίθετες κατευθύνσεις, εάν η τροχαιά είναι συμπληρωμένη, το αλγευρικό άθροισμα των ροπών των δύο ηλεκτρονίων είναι μηδέν  

Προφανώς, μια συμπληρωμένη τροχαιά δεν συνεισφέρει στην ολική ροπή του ατόμου (πράγμα επιθυμητό για την συνολική του ευστάθεια)

1s:AtomicOrbital n1 l0.png

 

 
 

2s:  \psi \begin{pmatrix} r, \theta, \phi \end{pmatrix} = \frac{1}{4 \sqrt{2 \pi}} \begin{pmatrix} 2 - \rho \end{pmatrix} e^{- \frac{\rho}{2}} . AtomicOrbital n2 l0.png

 
2px: n=2, \ell=1: \psi \begin{pmatrix} r, \theta, \phi \end{pmatrix} = \frac{1}{4 \sqrt{2 \pi}} re^{- \frac{\rho}{2}} \eta \mu \theta \sigma \upsilon \nu \phi .
2py: n=2, \ell=1: \psi \begin{pmatrix} r, \theta, \phi \end{pmatrix} = \frac{1}{4 \sqrt{2 \pi}} re^{- \frac{\rho}{2}} \eta \mu \theta \eta \mu \phi .              AtomicOrbital n2 l1.png
2pz: n=2, \ell=1: \psi \begin{pmatrix} r, \theta, \phi \end{pmatrix} = \frac{1}{4 \sqrt{2 \pi}} re^{- \frac{\rho}{2}} \sigma \upsilon \nu \phi
 
 
 
.
3s: n=3, \ell=0:  \psi \begin{pmatrix} r, \theta, \phi \end{pmatrix} = \frac{1}{81 \sqrt{3 \pi}} \begin{pmatrix} 27 - 18 \rho + 2 \rho^2 \end{pmatrix} e^{- \frac{\rho}{3}} AtomicOrbital n3 l0.png

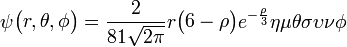3px: n=3, \ell=1: \psi \begin{pmatrix} r, \theta, \phi \end{pmatrix} = \frac{2}{81 \sqrt{2 \pi}} r \begin{pmatrix} 6 - \rho \end{pmatrix} e^{- \frac{\rho}{3}} \eta \mu \theta \sigma \upsilon \nu \phi .
3py: n=3, \ell=1: \psi \begin{pmatrix} r, \theta, \phi \end{pmatrix} = \frac{2}{81 \sqrt{2 \pi}} r \begin{pmatrix} 6 - \rho \end{pmatrix} e^{- \frac{\rho}{3}} \eta \mu \theta \eta \mu \phi .
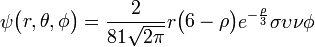
3pz: n=3, \ell=1: \psi \begin{pmatrix} r, \theta, \phi \end{pmatrix} = \frac{2}{81 \sqrt{2 \pi}} r \begin{pmatrix} 6 - \rho \end{pmatrix} e^{- \frac{\rho}{3}} \sigma \upsilon \nu \phi
 
     Αυτά είναι λοιπόν τα ατομικά τροχιακά ή αλλιώς οι τροχαιές όπως τις συνέλαβε αρχικά ο Bohr που δεν είναι βέβαια κυκλικές όμως είναι κοντά στην ιδέα που είχαν τότε. Βέβαια  εφ όσον τα τροχιακά προκύπτουν από πιο πολύπλοκες εξισώσεις, δεν έχουν το σχήμα που πρότειναν τότε το 1913, όμως η ιδέα τους ήταν γενικά σωστή ώστε τελειοποιήθηκε αργότερα
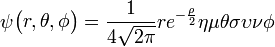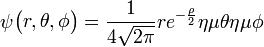