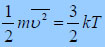Δήμητρα Σπανού συνταξιούχος καθηγήτρια Χημικός Δευτεροβάθμιας Εκπ/σης
υπό κατασκευή
ΕΙΣΑΓΩΓΗ
Πριν αρχίσουμε να περιγράφουμε την δράση της μάζας, θα πρέπει ξεκινήσουμε από την παρακάτω παραδοχή:
Η ιδέα της μάζα των υλικών σωμάτων -σαν απόλυτη αξία - (εφόσον αυτή θεωρείται σταθερή και αμετάβλητη ) πρέπει να επανεξεταστεί
Αρχικά επειδή αυτή η σταθερότητα και ακινησία δεν ισχύει στις μικροδιαστάσεις γιατί η μάζα απαρτίζεται από μικρότερα μέρη -τις δομικές μονάδες της_ που τις μετράμε σε διαστάσεις μικρότερης τάξης μεγέθους οι οποίες βρίσκονται σε διαρκή κίνηση
Όλα τα σώματα στην σύγχρονη Φυσική θεωρούνται συστήματα των δομικών τους μονάδων - των μικροσωματίδιων.
Ακόμη, και οι ιδιότητες των συστημάτων αυτών απορρέουν από τις ιδιότητες και τις μικροκαταστάσεις των σωματιδίων τους.
Αλλά ας θυμιθούμε συνοπτικά πως
ΟΙ ΔΡΑΣΕΙΣ ΤΩΝ ΣΩΜΑΤΙΔΙΩΝ ΕΝΟΣ ΣΥΣΤΗΜΑΤΟΣ ΔΙΝΟΥΝ ΜΑΚΡΟΣΚΟΠΙΚΑ ΑΠΟΤΕΛΕΣΜΑΤΑ
Τα σωματιδία που την αποτελούν τα υλικά σώματα βρίσκονται σε μια διαρκή δράση που περιλαμβάνει, ανάλογα και με την φυσική τους κατάσταση, τυχαίες ή καθορισμένες κινήσεις,
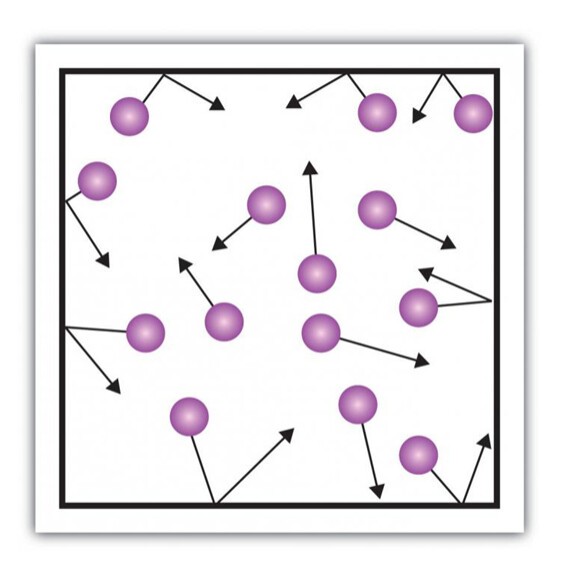Για να κάνουμε ευκολότερη την μελέτη τους ξεκινάμε από συστήματα μη αλληλεπιδρώντων σωματιδίων, που κινούνται διαγράφοντας μικρότερες ή μεγαλύτερες ευθίγραμμες τροχαιές και που ακόμα υπάρχουν συγκρούσεις μεταξύ τους (αλλά ελαστικές και αναποτελεσματικές που δεν αλλοιώνουν την φύση των σωματιδίων)
Σύμφωνα με την κινητική θεωρία ιδανικού αερίου, τα σωματίδια (άτομα ή μόρια) που το αποτελούν την αέρια μάζα, κινούνται ελεύθερα μέσα σε στο ακίνητο δοχείο που περιέχεται το αέριο και δεν αλληλεπιδρούν μεταζύ τους εκτός από πρακτικά στιγμιαίες ελαστικές συγκρούσεις και δεν υπάρχει απώλεια κινητικής ενέργειας
Ο συντελεστής τριβής μεταξύ τους είναι μηδέν και δεν υπάρχουν ελκτικές δυνάμεις μεταξύ τους
Θεωρητικά, τα μόρια του ιδανικού αερίου θεωρούνται μικρές σφαίρες χωρίς δομή και με όγκο αμεληταίο
Στην περίπτωση συστημάτων μη αλληλεπιδρώντων σωματιδίων, οι ταχύτητες και οι ενέργειές τους περιγράφονται από κατανομές πιθανοτήτων των Maxwell- Boltzman
H δράση των μικροσωματιδίων στον μικρόκοσμο εξηγεί τελικά και τα μακροσκοπικά αποτελέσματα της ύλης όπως μεταβολές στην πίεση στην θερμοxωρητικότητα ακόμα φυσικά, ηλεκτρικά και χημικά φαινόμενα.
Πριν αναφέρουμε κάποια περισσότερα για τις κατανομές Maxwell- Boltzman σε συστήματα μη αλληλεπιδρώντων σωματιδίων ας θυμηθούμε ότι, οι μακροσκοπικές ιδιότητες στα αέρια διατυπώθηκαν στην Κλασσική Φυσική οι νόμοι των αερίων από τους Boyle, Charles, Gay-Lussac στα μέσα του 17ου αιώνα.
Θεωρίες που περιέγραψαν τα μακροσκοπικά φαινόμενα στην ύλη, όπως η Μοριακή Κινητική Θεωρία της Ύλης που βασίστηκε σε θεωρίες που διατυπώθηκαν από επιστήμονες όπως ο Bernouli o R. Clausius. ο J. C. Maxwell- L. Boltzman, ο S. Arrhenius , ήρθαν αργότερα στο τέλος του 19ου αιώνα
Από αυτές τις θεωρίες που προηγήθηκαν της Μοριακής Κινητικής Θεωρίας σημειώνουμε τον
Bernouli, που διατύπωσε την ιδέα των μορίων των αερίων σαν ελαστικές σφαίρες, τον
R. Clausius, που διατύπωσε συμπεράσματα για την κίνηση των μορίων των αερίων. Τα σωματίδια αερίων δεν σταματούν ποτέ να κινούνται. Επίσης συγκρούονται μεταξύ τους και με τα τοιχώματα του δοχείου που περιέχεται, τους
J. C. Maxwell- L. Boltzman που προσπαθούν να εξηγήσουν τις πειραματικές παρατηρήσεις των αερίων από μικροσκοπική προοπτική
και ακόμη S. Arrhenius με την θεωρία των ενεργών συγκρούσεων
Σύμφωνα με αυτή τα σωματίδια που κινούνται και συγκρούονται μεταξύ τους έχουν συνολικά ένα ποσό ενέργειας την εσωτερική ενέργεια του σώματος
και στη Στατιστική Μηχανική
Η κινητική θεωρία δίνει τις σχέσεις μεταξύ των μικροκαταστάσεων και των μακροκαταστάσεων όπως
 |
|
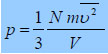που συνδέουν την πίεση τον όγκο την θερμοκρασία του συστήματος με την μέση ταχύτητα και την μέση κινητική ενέργεια των μορίων
Αν και η λογική όλων των συστημάτων σωματιδίων είναι πανομοιότυπη καθως και οι μαθηματικές εξισώσεις που μας επιτρέπουν την μελέτη τους, Οι διαστάσεις του συστήματος (της μάζας) στην οποία αναφερόμαστε διαφέρουν σημαντικά.
Η τάξη των διαστάσεων των δομικών μονάδων εξαρτάται από τις διαστάσεις του συστήματος (της μάζας) στην οποία αναφερόμαστε
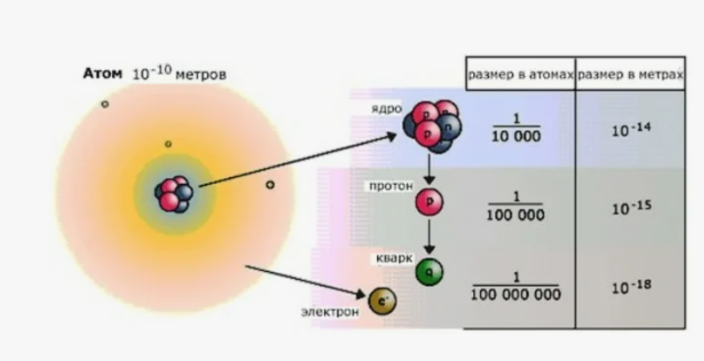Τα άτομα των χημικών στοιχείων της πραγματικής (για τις ανθρώπινες διαστάσεις ύλης) έχουν διάμετρο από 1 έως 5 .10-10 m (τάξης 10-10) και αν τα θεωρήσουμε συστήματα σωματιδίων, τα στοιχειώδη σωματίδια της μάζας του προέρχεται από τα οι δομικές τους μονάδες είναι τα
πρωτόνια και τα νετρόνια του πυρή να διαμέτρου της τάξης 10-15 και τα ηλεκτρόνια διαμέτρου της τάξης 10-18
Τα κουάρκς διαμέτρου περίπου της τάξης 10- 18 είναι τα στοιχειώδη σωματίδια για τα πρωτόνια και νετρόνια (που λέγονται αδρόνια) του πυρήνα
Οι πολύ μικρές διαστάσεις είναι δύσκολο να μελετηθούν καθώς και οι πολύ μεγάλες.
Για να ξεπεραστεί το πρόβλημα και να βρεθούν όσο το δυνατό γενικότερα αποτελέσματα χρησιμοποιούμε το θερμικού μήκους κύματος de Broglie
ώστε, γίνεται μια κατηγοριοποήση των διαφόρων συστημάτων σωματιδίων που δεν βασίζεται στην χρήση των γεωμετρικών διαστάσεών τους αλλά στο θερμικό μήκος κύματος
Η ΘΕΩΡΙΑ DE BROGLIE
Σύμφωνα με την θεωρία του de Broglie, κατά την οποία όλα τα
σωματίδια έχουν κυματική συμπεριφορά παράλληλα με την σωματιδιακή (όχι όμως ταυτόχρονα)
H ιδέα του de Broglie για την κυματοειδή φύση της ύλης ήταν η εξής:
μεταφορά από physics4u-Louis de Broglie
Στην διατριβή του ο Louis de Broglie αναφέρει τα εξής:
"Αφού τα φωτόνια δείχνουν συγχρόνως χαρακτηριστικές ιδιότητες σωματίων και κυμάτων, γιατί να μην συμβαίνει και το ίδιο με όλες τις μορφές της ύλης, γιατί δηλαδή τα σωματίδια να μη συμπεριφέρονται και ως κύματα".
αλλά η μελέτες του περιορίσθηκαν στην μελέτη της κυματοειδούς φύσης του ηλεκτρονίου
μεταφορά από physics4u-Louis de Broglie
Κατά τον de Broglie το ηλεκτρόνιο ή οποιοδήποτε άλλο σωματίδιο έχει κι' αυτό διττή υπόσταση. Είναι σωματίδιο με ορμή p και κύμα με μήκος λ. Η σχέση που τα συνδέει πρέπει να είναι ίδια με αυτή που ισχύει στα φωτόνια: 
ενώ η συχνότητα του μηχανικού κύματος θα δίνεται από τη σχέση: 
Από την θεωρία αυτή προκύπτει το μήκος κύματος de Broglie καθώς καi το θερμικό μήκος κύματος de Broglie
Το θερμικό μήκος κύματος de Broglie ή θερμικό μήκος κύματος de Broglie λth ή θερμικό μήκος κύματος Λ
είναι περίπου το μισό μήκος κύματος de Broglie των σωματιδίων σε ένα ιδανικό αέριο. Είναι καθοριστικό για να κατατάξουμε τα σωματίδια σε κατηγορίες.
Κάτω από αυτήν την προοπτική μπορούμε να διακρίνουμε κάποιες κατηγορίες για την περιγραφή της κίνησης των σωματιδίων καθώς και τις πιθανότητες κατανομής των ταχυτήτων τους και των ενέργειών τους (χωρίς αυτό να σημαίνει ότι η ιδέα αυτή δεν μπορεί να επεκταθή και για μελέτη άλλων πολύ μικρότερων ή μεγαλύτερων διαστάσεων συστήματα)
Γενικά μελετάμε περιπτώσεις στις οποίες:
- το σώμα μπορεί να εξεταστεί με τα πρότυπα της κλασσικής φυσικής ακόμα και στην οριακά ιδανική κατάσταση όπως είναι η αέρια φάση σωματιδίων που δεν αλληλεπιδρούν
- ή όταν οι προδιαγραφές του είναι τέτοιες που κυριαρχούν τα κβαντικά φαινόμενα και περιγάραφεται καλύτερα από την κβαντική θεωρία
- ή ακόμα αν τα χαρακτηριστικά φυσικά μεγέθη τους πλησιάζουν αυτά των φωτονίων τότε αδυνατώντας να διακρίνουμε την μάζα, λέμε ότι έχουμε σώματα χωρίς μάζα και χρησιμοποιούμε το θερμικό μήκος κύματος αυτών και περιγράφουμε την συμπεριφορά τους μέσα από την κβαντική θεωρία
1η ΠΕΡΙΠΤΩΣΗ Οι στατιστικές Fermy-Dirack είναι κβαντικές στατιστικές που εφαρμόζονται σε συστήματα πανομοιότυπων φερμιονίων που υπακούουν στην αρχή του Pauli (μια κβαντική κατάσταση δεν μπορεί να καταληφθεί από περισσότερα από ένα σωματίδια).
και ισχύουν σε σε χαμηλές θερμοκρασίες ή σε υψηλές συγκεντρώσεις και όταν κυριαρχούν τα κβαντικά φαινόμενα
Λ<<<(V/N)1/3 ή V/NΛ3>>>1
2η ΠΕΡΙΠΤΩΣΗ Οι στατιστικές Bose-Einstein είναι κβαντικές στατιστικές που εφαρμόζονται σε συστήματα πανομοιότυπων μποζονίων και δεν υπακούουν στην αρχή του Pauli ( περισσότερα από ένα σωματίδια μπορεί να βρεθούν στην ίδια κβαντική κατάσταση )
και ισχύουν σε σε χαμηλές θερμοκρασίες ή σε υψηλές συγκεντρώσεις και όταν κυριαρχούν τα κβαντικά φαινόμενα
για Λ>>>(V/N)1/3 ή V/NΛ3<<<1
3η ΠΕΡΙΠΤΩΣΗ Στις στατιστικές Maxwell-Boltzman ισχύουν σε υψηλές θερμοκρασίες (και περιβάλλοντος) και χαμηλές συγκεντρώσεις σωματιδίων που δεν αλληλεπιδρούν
για Λ>>>(V/N)1/3
Σύμφωνα με την κινητική θεωρία ιδανικού αερίου, τα σωματίδια (άτομα ή μόρια) που το αποτελούν κινούνται ελεύθερα μέσα σε ένα ακίνητο δοχείο και δεν αλληλεπιδρούν μεταζύ τους εκτός από πρακτικά στιγμιαίες συγκρούσεις κατά τις οποίες ανταλλάσουν ενέργεια και ορμή.
Δήμητρα Σπανού
αναλυτικότερα περιγράφονται
ακατέργαστο
Η κίνηση δράση και η ενέργεια για τα μικροσωματίδια που αποτελούν ένα σύστημα σωματιδίων, είναι σημαντικό να μελετηθούν, ιδιαίτερα στο θέμα της κατανομής των ενεργειών στα σωματίδια αυτά, γιατί αυτό είναι ο τρόπος να υπολογιστεί η συνολική ενέργεια του συστήματος και όλα τα μακροσκοπικά φαινόμενα που είναι συνέπεια των συγκρούσεων μεταξύ των σωματιδίων, των ενεργών συγκρούσεων και των χημικών αντιδράσεων στην συνέχεια
ΠΗΓΕΣ
Κατανομή Μάξγουελ-Μπόλτσμαν - Βικιπαίδεια
Κατανομή Maxwell-Boltzmann | Science Wiki | Fandom
Η κίνηση ως μορφή ύπαρξης της ύλης Χημεία
Θερμικό μήκος κύματος - Βικιπαίδεια
Επίδραση της θερμοκρασίας. Εξίσωση Arrhenius