ΠΕΡΙΟΔΙΚΑ ΦΑΙΝΟΜΕΝΑ: 1ο μέρος. Ταλαντώσεις. Μηχανικές ταλαντώσεις και εξίσωση ελατηρίου, απόσβεση. Διεγερμένες ταλαντώσεις: Ηλεκτρικές ταλαντώσεις. Ηλεκτρομαγνητικές ταλαντώσεις

της Δήμητρας Σπανού Χημικού καθηγήτριας στο 1ο Γυμνάσιο Δάφνης

υπό κατασκευή

ΠΕΡΙΟΔΙΚΑ ΦΑΙΝΟΜΕΝΑ

Υπάρχουν φαινόμενα στη φυσική που χαρακτηρίζονται από κυκλικές αλλαγές και οι  φυσικές ποσότητες που τα χαρακτηρίζουν το φαινόμενο μεταβάλλονται περιοδικά  στον χώρο και στον χρόνο. Τα φαινόμενα αυτ χαρακτηρίζονται περιοδικά. Τέτοια φαινόμενα συναντάμε στη φύση όπως είναι η αλλαγή των εποχών, το πέταγμα των πουλιών, η καρποφορία, η εκπομπή ακτινοβολίας από τα παλσαρ

 Τέτοια φαινόμενα  συναντάμε στην μηχανική, όταν μελετάμε την κίνηση του ελατηρίου, του εκκρεμούς, το έμβολο σε κινητήρες εσωτερικής καύσης, δονήσεις του φλοιού της γης  σε σεισμούς, κατακόρυφη ταλάντωση σώματος βυθισμένου σε υγρό κ.α όπου έχουμε περιοδική μετατροπή της κινητικής και της μηχανικής ενέργειας. 

παρόμοια, στον ηλεκτρομαγνητισμό,  έχομε ηλεκτρομαγνητικές ταλαντώσεις,  (κύκλωμα εναλλασσόμενου ρεύματος, ταλαντώσεις πεδίου) και ηλεκτρομαγνητικές δονήσεις.

Περιοδικότητα επίσηε έχουμε και με την διάδοση κυμάτων:

Σε μηχανικά κύματα όπως  η διάδοση του ήχου ή 

ηλεκτρομαγνητικά όπως τα  σε ραδιοκύματα, μικροκύματα, υπέρυθρη ακτινοβολία, ορατό φως, υπεριώδης ακτινοβολία, ακτίνες Χ, ακτίνες γ

Οι ταλαντώσεις μηχανικής φύσεως και οι ταλαντώσεις ηλεκτρομαγνητικής φύσεως υπόκεινται στους ίδιους ποσοτικούς νόμους

ΤΑΛΑΝΤΩΣΕΙΣ ΚΑΙ ΚΥΜΑΤΑ 

Όπως είπαμε στις περιοδικές κινήσεις αλλάζουν κυκλικά. Όταν πρόκειται για ταλαντώσεις οι τιμές των φυσικών μεγεθών  αλλάζουν περιοδικά στον χρόνο, ενώ στα κύματα οι τιμές των φυσικών μεγεθών αλλάζουν περιοδικά στον χώρο και στον χρόνο

Οι ταλαντώσεις αλλά και στα κύματα, οι τιμές των φυσικών μεγεθών αλλάζουν κυκλικά. 

Στις ταλαντώσεις η φυσική ποσότητα ταλαντώνεται μεταξύ δύο σημείων μεγίστης απομάκρυνσης από τη θέση ισορροπίας, αφού οι χωρικές σσυντεταγμένες είναι σταθερές.

Σστα κύματα  έχουμε μια ορισμένη κατανομή της φυσικής ποσότητας στον χώρο, αφού με εναλλαγη μεγίστων και ελαχίστων.

Οι ταλαντώσεις είναι μια κυκλική διαδικασία που επαναλαμβάνεται με την πάροδο του χρόνου. Αν θεωρήσουμε ένα σημείο που κινείται κατά μήκος ενός μοναδιαίου κύκλου, τότε η προβολή του πάνω σε διάμετρο του κύκλου, χρησιμοποιείται για τη γραφική απεικόνηση των ταλαντώσεων

Στις ταλαντώσεις υπάρχει μια κατάσταση ισορροπίας και  συμβαίνει διαρκώς  μια διαδικασία αλλαγής καταστάσεων κοντά σε σημείο ισσορροπίας που επαναλαμβάνεται στον χρόνο. Σχετίζονται σχεδόν πάντα με τον μετασχηματισμό της ενέργειας από μια μορφή σε άλλη.

Εάν οι τιμές των φυσικών μεγεθών που χαρακτηρίζουν το ταλαντευόμενο σύστημα επαναλαμβάνονται σε τακτά χρονικά διαστήματα ονομάζονται περιοδικές.  

ΑΡΜΟΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ

Εάν οι διακυμάνσεις δίνονται από τις σχέσεις   ή  

ονομάζονται αρμονικές ταλαντώσεις

Στις αρμονικές ταλαντώσεις από την ενέργεια προκύπτει η εξίσωση που περιγράφει τα φυσικά ταλαντούμενα συστήματα είναι: α+ ω² x = 0  ή 

H λύση της εξίσωσης είναι η εξίσωση κίνησης για τις αρμονικές ταλαντώσεις είναι x =  A cos(ωt+φ_ο)

ω είναι η κυκλική συχνότητα (που εξαρτάται από τις ιδιότητες του συστήματος) και  Α είναι το πλάτος μετατόπισης φάση είναι η γωνία ωt+φ_ο

( που καθορίζονται με  τον τρόπο με τον οποίο το σύστημα τέθηκε εκτός ισορροπίας ) 

αντίστοιχα υπάρχουν εξισώσεις που περιγράφουν την εξάρτηση της ταχύτητας υ και της επιτάυνσης α από τον χρόνο      

Αρμονικές ταλαντώσεις έχουμε σε διάφορα ταλαντούμενα συστήματα όπως στο μαθηματικό εκκρεμές και στις ηλεκτρικές ταλαντώσεις κυκλώματος LC αν δεν υπάρχει απόσβεση.

Ενεργειακά οι σχέσεις δίνονται   και αν Uo = Q_o/C ,  Io=ω Qo

από εδώ προκύπτει εξισωση ανάλογη με των μηχανικών ταλαντούμενων συστημάτων ω² =1/LC που σαν

 διαφορική 2ου βαθμού γράφεται : d²φ/dt² =1/LC

Στις ηλεκτρικές ταλαντώσεις μεταβάλλονται αρμονικά η ένταση Ι του ηλεκτρικού ρεύματος και το φορτίο q του πυκνωτή

i=-Iημωt   και q=Qσυνωt

Οι ταλαντώσεις σχετίζονται στενά με τα κύματα και γι αυτό η θεωρία που έχει επικρατήσει είναι η θεωρία των ταλαντώσεων και των κυμάτων που  ασχολειται με την μελέτη περιοδικών φαινομένων

Οι ελεύθερες  ταλαντώσεις που συμβαίνουν χωρίς περιοδικές εξωτερικές επιδράσεις και η συχνότητά τους λέγεται ιδιοσυχνότητα 

Διεγερμένες ταλαντώσεις συμβαίνουν υπό την επίδραση εξωτερικής περιοδικής επιρροής

Ταλάντωση που προκαλείται σε ένα σύστημα από περιοδική εξωτερική δύναμη που προσφέρει ενέργεια στο σύστημα και ονομάζεται διεγέρτης

ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ

Στις μηχανικές ταλαντώσεις έχουμε μια κατάσταση ισορροπίας και αν το σύστημα που ταλαντεύεται ισσορροπεί σε κάποιο σημείο (σταθερή κατάσταση). Εάν απομακρυνθεί από αυτήν, αναπτύσεται δύναμη που το επιστρέφει όμως συνεχίζει λογω αδράνειας στην αντίθετη κατεύθυνση. 

Έτσι οι κινήσεις αυτές  επαναλαμβάνονται περιοδικά στον χρόνο, 

και πάντα υπάρχει μια φυσική ποσότητα (που χαρακτηρίζει το φαινόμενο) η οποία  αλλάζει. Στο ελατήριο για παράδειγμα αλλάζει το διάνυσμα της απομάκρυνσης απο τη θέση ισσορροπίας,  ενώ στις ηλεκτρικές ταλαντώσεις  αλλάζει κατεύθυνση είναι το ηλεκτρικό ρεύμα. Οι τιμές που παίρνουν σε συνάρτηση με τον χρόνο δίνονται από μαθηματικές σχέσεις τις εξισώσεις της ταλάντωσης

Οι ταλαντώσεις περιγράφονται από διαφορικές μαθηματικές εξισώσεις

ΕΞΑΝΑΓΚΑΣΜΕΝΗ ΤΑΛΑΝΤΩΣΗ

Διακρίνουμε την ιδιοσυχνότητα του ταλαντούμενου συστήματος και την συχνότητα του διεγέρτη. Όταν η συχνότητα του διεγέερτη γίνει ίση με την ιδιοσυχνότητα του ταλαντούμενου συστήματος τότε το σύστημα παίρνει όλη την ενέργεια του διεγέρτη και έχουμε σσυντονισμό με το μέγιστο πλάτος στην εξαναγκασμένη ταλάντωση. Διαφορετικά, η εξαναγκασμένη ταλάντωση έχει  

α. Σύστημα ταλάντωσής. Ελατήριο. Ελεύθερη ταλάντωση. Εξίσωση ελατηρίου

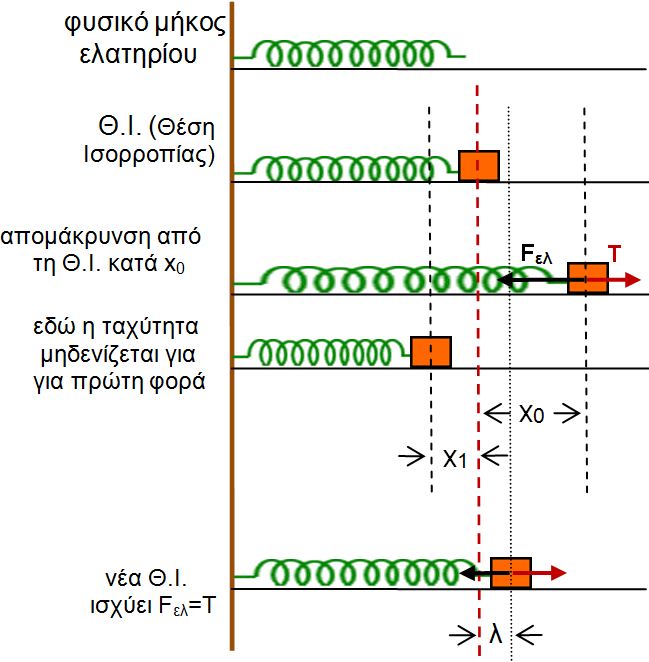Οι δυνάμεις στον ταλαντωτη είναι η τάση Τ = -kx  (Η Δύναμη που ασκείται στο ελατήριο για να επιμηκυνθει κατά x είναι kx) 

 Η δύναμη επαναφοράς προσδίδει επιτάχυνση α F επ = mα.

H μετατόπιση είναι x 

H ταχύτητα στον ταλαντωτη είναι η πρώτη παράγωγος της μετατόπισης dx/dt =y (ταχύτητα)

Η επιτάχυνση στον αρμονική ταλαντωτή θεωρείται η δεύτερη παράγωγος της μετατόπισης ίση με α= d²x/dt² 

 

Η δύναμης επαναφοράς είναι ky ( k σταθερά του ελατηρίου)ενώ η  Γνωρίζουμε πως η επιτάχυνση είναι η δεύτερη παράγωγος του διαστήματος ως προς χρόνο. Άρα  F επ = md²x/dt²)

 

 F επ -Τ =0 και η εξίσωση που το περιγράφει είναι διαφορική 2ας τάξης:

 

md²x/dt²   - kx  =0  

 

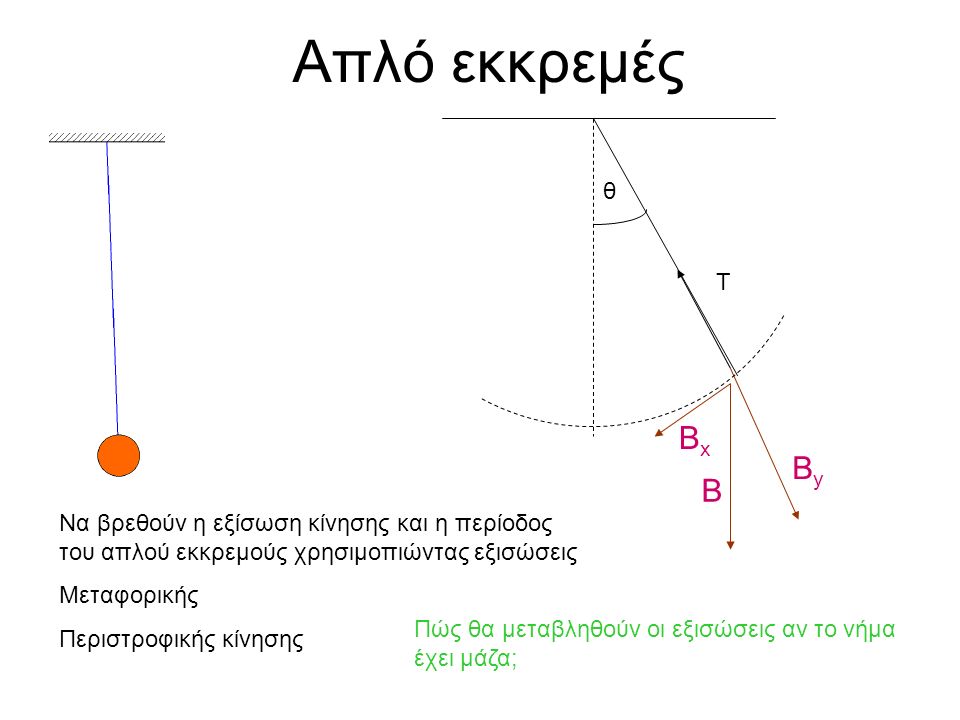
β.σύστημα απλής αρμονικής  ταλάντωσης : Εκκρεμές. Εξίσωση Εκκρεμούς (αρμονικός τακαντωτής)

Το εκκρεμές είναι στερεό σώμα μέσα σε βαρυτικό πεδίο που μπορεί να περιστρέφεται γύρω από οριζόντιο άξονα που δεν περνά από το κέντρο βάρους του.  Η θέση ισσορροπίας του είναι η κατακόρυφη ευθεία που περνά από το κέντρο βάρους του. Εάν εκκτραπεί κάνει ταλάντωση.

Το μαθηματικό εκκρεμές είναι ένα ιδανικό μοντέλο εκκρεμούς και αποτελείται από σημειακή μάζα, αβαρές νήμα που κρέμεται από σταθερό σημείο και εκτελεί ταλαντώσεις όταν εκτρέπεται από τη θέση ισσορροπίας του.

 Η δύναμη επαναφοράς του είναι F= -m.g. sinθ  και αφού g. sinθ είναι η συνιστώσα της επιτάχχυνσης της βαρύτητας στην τροχαιά κίνησης του σώματος, έχουμε

  F= -m.g. sinθ = m.dS ²/dt²

 

Επειδή για μικρές γωνίες ημθ=θ η εξίσωση και η διαφορική εξίσωση 2ας τάξης που  περιγράφει την μαθηματική ταλάντωση 

γίνεται:   dS ²/dt²  +( g/l ) θ =0

Η περίοδος 

Στο φυσικό εκκρεμές  η  περίοδος της ταλάντωσης  ειναι    όπου Ι είναι η ροπή αδρανείας , 

 

 

ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ

Εδώ υπάρχει μια διάταξη που περιλαμβάνει ένα πηνίο σε σύνδεση με έναν πυκνωτή με αρχική ενέργεια του πεδίου του πυκνωτή 

U_E= 1/2 Q²/C που με την εκφόρτι9ση του πυκνωτή μετατρέπεται σε ενέργεια μαγνητικού πεδίου στο πηνίο 

 δημιουργεί περιοδικές μεταβολές στις τιμές  ηλεκτρικών μεγέθη που είναι: το ηλεκτρικό φορτίο q το ηλεκτρικό ρεύμα Ι και η ηλεκτρική τάση V.

 To εναλλασσόμενο ηλεκτρικό ρεύμα είναι ένα περιοδικά εναλλασσόμενο ρεύμα που αλλάζει σε μέγεθος και σε κατεύθυνση. Διακρίνουμε την στιγμιαία ένταση και την μέγιστη ένταση Ι_m που λέγεται και πλάτος του εναλλασσόμενου ρεύματος 

Αν το εναλλασσόμενο ρεύμα επαναλαμβάνει τον πλήρη κύκλο των αλλ αγών σε τακτά χρονικά διαστήματα επιστρέφοντας στην αρχική τιμή έχουμε ένα περιοδικό εναλλασσόμενο ρεύμα και εάν αλλάζει σύμφωνα με τον αρμονικό νόμο έχουμε ένα ημιτονοειδές περιοδικό εναλλασσόμενο ρεύμα

Το ημιτονοειδές ρεύμα θεωρείται στοιχειώδες, δηλαδή δεν μπορεί να αποσυντεθεί σε άλλα απλούστερα εναλλασσόμενα ρεύματα

 

ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ

Περιοδικές αλλαγές όπου η  ενέργεια ηλεκτρικού πεδίου που εκφράζεται από το διανυσματικό μέγεθος της Έντασης ηλεκτρικού πεδίου Ε μετατρέπεται περιοδικά σε ενέργεια μαγνητικού πεδίου που εκφράζεται από την ένταση μαγνητικου πεδίου Β

 

 

γ. Ηλεκτρικές ταλαντώσεις LC

Παράδειγμα το κύκλωμα RC 

Κύκλωμα L C Ηλεκτρικές ταλαντώσεις

U_L +U_c =0

αν q=y   x=t                 

Η Επαγωγική τάση που προκείται  U_L = Εεπ =  -L.dI / dt.   = -Ld^₂q / dt ²      (dy/dx = dI / dt) Το ηλεκτρικό ρεύμα που διαρέει το κύκλωμα  είνα    I = dq / dt  

Hτάση στα άκρα του πυκνωτή είναι Uc = q/C

αντικαθιστώντας έχουμε q/C  -Ld^₂q / dt ² =0  

 

2. 2ης τάξης τύπου y΄΄ +  p₁y΄ + p_oy =0

Παράδειγμα 

Κύκλωμα R L C Ηλεκτρικές ταλαντώσεις

U_R+U_L +U_c =0

 

αν q=y   x=t                

-Η Επαγωγική τάση που προκείται Εεπ =  -L.dI / dt.  = IR + IR_E

  dy/dx = .dI / dt

Το ηλεκτρικό ρεύμα που διαρέει το κύκλωμα  είνα    I = dq / dt   και 

-η Τάση στα άκρα της αντίστασης είναι U_R = IR= dq / dt .R

Αντικαθιστώντας έχουμε    Εεπ = -  L. (d )(dq / dt)/ dt   --> -  L. (d ²q / dt²)

-H τάση στα άκρα του πυκνωτή είναι Uc = dq / dt .R

H ΔΕ γίνρται -  L. (d ²q / dt²)  + dq / dt .R  + dq / dt .R =0       (αy΄΄ + βy΄+γy =0)

 

Στο πρόβλημα, του αρμονικού ταλαντωτή με απόσβεση

Σύστημα μάζας- ελατηρίου ισχύει ο νόμος του Hooke και υπάρχει ένας γραμμικός όρος απόσβεσης. Η Δύναμη επαναφοράς του ελατηρίου είναι ανάλογη με την απομάκρυνση από την θέση ισορροπίας και η δύναμη απόσβεσης είναι ανάλογη της ταχύτητας της κίνησης dy/dx =y΄.

Fελ = -ky και Fαπόσβεσης = -αy΄

Η συνολική δύναμη είναι F = Fελ  + Fαπόσβεσης   --> ma =  -ky  -αy΄ όμως a =d²y/dt και y΄ =dy/dt και έχουμε την ΔΕ

md²y/dt²  -αdy/dt - ky =0

Στο πρόβλημα του αρμονικού ταλαντωτή καταλήγουμε στην διαφορική εξίσωση Στο πρόβλημα του αρμονικού ταλαντωτή καταλήγουμε στην διαφορική εξίσωση     αν  πρόκειται για συνάρτηση    της μετατόπισης  σε  σχέση με τον χρόνο     

H μετατόπιση είναι x 

-Η δύναμη στον ταλαντωτη είναι F= mα. 

Η επιτάχυνση στον αρμονική ταλαντωτή θεωρείται η δεύτερη παράγωγος της μετατόπισης ίση με α= d²x/dt² όπου  F= m d²x/dt²

Η επιτάχυνση στον αρμονική ταλαντωτή θεωρείται επίσης  η πρώτη παράγωγος της ταχύτητας α= dy/dt  

-Η δύναμης επαναφοράς T είναι ky ( k σταθερά του ελατηρίου) T = -ky

-H ταχύτητα στον ταλαντωτη είναι η πρώτη παράγωγος της μετατόπισης dx/dt =y (ταχύτητα)

Η απόσβεση N λόγω τριβών ή άλλης εξωτερικής αιτίας, θεωρείται ανάλογη της ταχύτητας (b.dy/dx ) b σταθερά απόσβεσης  N=(b.dy/dx

Έτσι

               

      

m d²x/dt²= -b.dy/dx - kx        

dy/dt  = -b/m(dx/dt)- (k/m) x 

dy/dt  = = -b(dx/dt)- k x

dy/dt  = -by- k x  

 

επειδή b2<< 4k  προσεγγοστικά

 

dy/dt = - [x(b(y/x)+ k )]/y

 

θέτουμε y/x =R(x)  οπ'οτε y=R(x)x

μετασχηματίζουμε

dy/dt = R + x (dR/dx)  και 

ολοκληρώνουμε

 και καταλήγουμε σε τελική λύση 

1/2 ln[y²/x²  +b.y/x +k] - b/2 . 1/(k-b²4)^1/2 tan^-1 [(y/x + b/2 )/(k- b²/4)^1/2] = -lnx + c

 

                                                                                   

 

 2ης τάξης τύπου y΄΄ +  p₁y΄ + p_oy = f(x)

Εξαρτημένη ταλάντωση

Κίνηση αρμονικού ταλαντωτή με απόσβεση που δέχεται εξωτερική διέγερση f(x)

αν   x=t   το  f(x) είναι  f(t)

δουλρ΄ύοντας ανάλογα έχουμε 

md²y/dt²  -αdy/dt - ky =f(t)

                        

Δήμητρα Σπανού