Αρχική Σελίδα > Η ΔΡΑΣΗ ΤΗΣ ΜΑΖΑΣ ΣΤΑΤΙΣΤΙΚΗ ΕΠΙΣΤΗΜΗ. ΟΙ ΚΑΤΑΝΟΜΕΣ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΦΥΣΙΚΗ Μέρος 2ο Μαθηματική Φυσική: Η Εξίσωση του Liouville.. Διακριτές και συνεχείς κατανομές. η μέση τιμή, το στατιστικό άθροισμα, η απόκλιση, το στατιστικό βάρος κ.α.

Η ΔΡΑΣΗ ΤΗΣ ΜΑΖΑΣ ΣΤΑΤΙΣΤΙΚΗ ΕΠΙΣΤΗΜΗ. ΟΙ ΚΑΤΑΝΟΜΕΣ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΦΥΣΙΚΗ Μέρος 2ο Μαθηματική Φυσική: Η Εξίσωση του Liouville.. Διακριτές και συνεχείς κατανομές. η μέση τιμή, το στατιστικό άθροισμα, η απόκλιση, το στατιστικό βάρος κ.α.

Δήμητρα Σπανού καθηγήτρια χημικός, συνταξιούχος Δευτερο/ιας Εκπ/σης από 30-6-2025

υπό κατασκευή

ΕΙΣΑΓΩΓΗ

Πριν αρχίσω να αναφέρομαι στις αλληλεπιδράσεις των σωματιδίων που θα επιφέρουν εξωτερικά μακροσκοπικές μεταβολές στην μάζα των σωμάτων θα πρέπει να σταθούμε στον μικρόκοσμο των σωματιδίων της ύλης. Εκεί η μελέτη της συμπεριφοράς των σωματιδίων των κινήσεων και των αλληλεπιδράσεων θα δώσει τα στοιχεία για τον προσδιορισμό των εξωτερικών παραμέτρων.

Αυτά είναι θέματα που αφορούν την Επιστήμη της Στατιστικής που ασχολείται με την συλλογή και ανάλυση δεδομένων που διευκολύνουν την μελέτη και επεξεργασία προβλημάτων διαφόρων κλάδων της επιστήμης . Πιο συγκεκριμένα εδώ η Στατιστική Φυσική συστημάτων σωματιδίων χρησιμοποιεί κατά πολύ τις εξισώσεις, τα στατιστικά στοιχεία και κατανομές στην μελέτη τους.

Η γνώση της κατανομής των σωματιδίων σε ένα σύστημα καθιστά δυνατή την εύρεση των μέσων τιμών διαφόρων χαρακτηριστικών ενός θερμοδυναμικού συστήματος χρησιμοποιώντας τον τύπο της μαθηματικής προσδοκίας Ε[Χ] ή Μ[Χ] $\mathbb {E} [X]$

$\mathbb {E} [X]$

Η ΕΞΙΣΩΣΗ LIOUVILLE

Ο Joseph Liouville (1809-1882) ήταν Γάλλος μαθηματικός. Διορίστηκε καθηγητής στο Ecole Polytecηnique το 1838. Εργάστηκε σε διάφορα πεδία των μαθηματικών συμπεριλαμβανομένης και της μαθηματικής φυσικής, όπου είχε δύο θεμελιώδεις συνεισφορές:

την θεωρία Sturm -Liouville για την επίλυση ορισμένων ολοκληρωτικών εξισώσεων με την ανάπτυξη σε ιδιοσυναρτήσεις

το Θεώρημα Liouville : Η χρονική εξέλιξη είναι το μέτρο για τη διατήρηση ενός Χαμιλτιανού συστήματος. Το θεώρημα ανακοινώνεται με απλότητα το 1853 και δημοσιεύεται το 1855. Ιδέες γύρω από αυτό το θέμα είχε επεξεργαστεί και δημοσιεύσει το 1842-43 ο Jacobi. To 1978 έχουμε μια νεώτερη έκδοση και ερμηνεία από τον V. Arnold και αναφέρεται σαν θεώρημα Arnold- Jacobi

H εξίσωση Liouville περιγράφει την χρονική εξέλιξη της συνάρτησης κατανομής (πυκνότητα πιθανότητας)του Χαμιλτονιανού συστήματος

(Στην Χαμιλτιανή δυναμική ο Liouville εισήγαγε την έννοια της μεταβλητής γωνίας δράσης)

Η ολοκληρωσιμότητα κατά Liouville στα Χαμιλτιανά συστήματα προυποθέτει από την διάσταση του χώρου των φάσεων, να συμπεριλάβουμε στην ανάλυση μόνο τις n διατηρήσιμες ποσότητες F_i που εξαρτώνται από τον χρόνο και να αγνοήσουμε τις υπόλοιπες από το συνολο των 2n διαστάσεων του χώρου των φάσεων

Στην γλώσσα του Liouville και του Jacobi οι ποσότητες Fi είναι οι νέες ορμές

Oi F_i που επιλέγουμε πρέπει να πληρούν προυποθέσεις ήτοι: να είναι ανεξάρτητες,

αντιστρέψιμες, (det ∂Fi ∂pj ̸ =0) όπου F = (F1,··· ,Fn)

και για κάθε i, j, να ισχύει [Fi, Fj] = 0

Υπό τις προυποθέσεις αυτές η Χαμιλτονιανή μπορεί να θεωρηθεί ως συνάρτηση των p,F και να γραφεί:

H(q,F,t) def = H(q,p(q,F,t),t) . ώστε ορίζεται νέα συνάρτηση -γενήτορας η V(q,F,t) και η σχέση

ηLdt=p(q,F,t)·dq−H(q,F,t)dt είναι τέλειο διαφορικό συνάρτησης V(q,F,t)

για μαθηματικές λεπτομέριες

eclass.uoa.gr/modules/document/file.php/PHYS181/%CE%94%CE%B9%CE%B1%CE%BB%CE%AD%CE%BE%CE%B5%CE%B9%CF%82%20%CE%BA%CE%B1%CE%B9%20%CE%A5%CE%BB%CE%B9%CE%BA%CF%8C%202020-2021/Integrability.pdf

ΚΑΠΟΙΕΣ ΜΑΘΗΜΑΤΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΕΙ Η ΣΤΑΤΙΣΤΙΚΗ ΜΗΧΑΝΙΚΗ ΚΑΙ ΤΑ ΔΙΑΓΡΑΜΜΑΤΑ ΤΟΥΣ

Η ΣΥΝΑΡΤΗΣΗ

Αποτελείται από δύο κλάδους συμμετρικούς ως προς τον άξονα ψ ψ' Εικόνα

Η ΕΚΘΕΤΙΚΗ ΣΥΝΑΡΤΗΣΗ Εικόνα

Εικόνα Για κάθε x E R ορίζεται η f(x) =α^xπου λέγεται εκθετική συνάρτηση με βάση α διάφορο από το μηδέν. Για α>1 την γραφική παράσταση στα αριστερ

Για 0<α<1 έχουμε την παράσταση στα αριστερα γνησίως αύξουσα στο R

Για 0<α<1 έχουμε την παράσταση στα δεξιά, γνησίως φθίνουσα στο R

Σε πολλές εφαρμογές χρησιμοποιείται η εκθετική συνάρτηση

f(x) η $y=e^{x}$ ή expx και e=2.718281828

Είναι αντιστρέψιμη και η αντίστροφη είναι lnx.ισχύει επίσης ⁠ $\exp(x+y)=\exp x\cdot \exp y$ οπότε $\ln(x\cdot y)=\ln x+\ln y$ ⁠. ή $e^{x+y}=e^{x}\cdot e^{y}$ .

Η πρώτη παράγωγός της είναι η ίδια η συνάρτηση. f(x)΄= f(x) ή ${\operatorname {d} \over \operatorname {d} x}e^{x}=e^{x}$

$f(x)=c\cdot e^{kx}$ τότε η πρώτη παράγωγος

ΟΙ ΚΑΤΑΝΟΜΕΣ ΣΤΗΝ ΕΠΙΣΤΗΜΗ ΤΗΣ ΣΤΑΤΙΣΤΙΚΗΣ

Ένας βασικός κλάδος της Επιστήμης της Στατιστικής είνα οι κατανομές που αποτελούν ένα μαθηματικό υπόδειγμα μοντελοποίησης των στατιστικών δεδομένων. Αυτό κάνει την δουλειά των ερευνητών ευκολότερη γιατί μια σειρά από δεδομένα μπορούν να προσομοιωθούν με βάση ένα μαθηματικό μοντέλο με συγκεκριμένες ιδιότητες. Με τον τρόπο αυτό μπορούν να προβλεφθούν μελλοντικές τιμές των δεδομένων ή να βρεθούν χρήσιμα μεγέθη όπως η μέση τιμή, διασπορά κ.λ.π.

Μαθηματικά μεγέθη που ορίζονται και χρησιμοποιούνται στις στατιστικές κατανομές

Μαθηματικά μεγέθη που ορίζονται και χρησιμοποιούνται στις στατιστικές κατανομές είναι τα :

Η αναμενόμενη τιμή η/και η μέση τιμή, το στατιστικό άθροισμα, η απόκλιση, το στατιστικό βάρος κ.α.

Η Αναμενώμενη Τιμή ή Μαθηματική Προσδοκία Ε[Χ] ή Μ[Χ]

Όταν θέλουμε να υπολογίσουμε την μέση τιμή κατανομής πιθανότητας πριν την συλλογή δεδομένων χρησιμοποιούμε την αναμενόμενη τιμή

Από τις πιθανότητες των πιθανών τιμών παίρνουμε την μέση τιμή μιας τυχαίας μεταβλητής. Συμβολίζεται με Ε[Χ] στην Γερμανική βιβλιογραφία και Μ [Χ] στην Ρώσικη. Η μαθηματική προσδοκία αθροίσματος n τυχαίων μεταβλητών είναι np αν η τυχαία μεταβλητή παίρνει μόνο τιμές 0 και 1

Η διάμεσος

Είναι η μεσαία τιμή στο σύνολο των παρατηρήσεων . Για 2n δεδομένα η διάμεσος είναι: (xn + xn+1)/2

Μέση τιμή μ και αριθμητική μέση τιμή

Η μέση τιμή (στατιστικό) ορίζεται από τον τύπο ∑i=1= N xi /N

Η αριθμητική μέση τιμή είναι το άθροισμα καταγεγραμένων τιμών Χ μιας μεταβλητής x διά τον αριθμό τους

Ο μέσος όρος

Όταν θέλουμε να υπολογίσουμε την μέση τιμή ενός δεδομένου δείγματος χρησιμοποιούμε τον μέσο όρο. Είναι η μέση τιμή των μετρήσεων του δείγματος

. Στην πράξη η αναμενώμενη τιμή συνήθως εκτιμάται ως ο αριθμητικός μέσος όρος Δηλαδή,

${\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}={\frac {1}{n}}(x_{1}+\ldots +x_{n})$

μέγεθος δείγματος, χi σρτοιχείο επιλογής

Υπολογίζεται προσθέτοντας όλες τις τιμές ενός συνόλου παρατηρήσεων και διαιρώντας το σύνολο με τον αριθμό των παρατηρήσεων

Κάποα παραδείγματα μέσης τιμής κατανομών

Σε μιας εκθετική κατανομή τυχαίας μεταβλητής Χ δίνεται από τον τύπο: $\mathrm {E} [X]={\frac {1}{\lambda }}.\!$

Στην κατανομή Poisson η μέση τιμή είναι περίπου ίση με την μέση τιμή λ της εμφανίσεως ενός γεγονότος σε συγκεκριμένο χρόνο ή χώρο

Στην κανονική κατανομή έχει τιμή 0

κ.λ.π.

το Στατιστικό Άθροισμα

Η συνάρτηση κατανομής Ζ που ονομάζεται Στατιστικό Άθροισμα το οποίο κανονικοποιεί την κατανομή ώστε το άθροισμα όλων των πιθανών καταστάσεων να είναι ίσο με 1 Ζ = ∑ie−βΕi

Η συνάρτηση κατανομής Ζ είναι σημαντική γιατί από αυτό το σύνολο εξαρτώνται θερμοδυναμικά μεγέθη του συστήματος όπως η πίεση, η ελεύθερη ενέργεια , η εντροπία και η πίεση

Για να κατανοήσουμε το στατιστικό άθροισμα αναφέρουμε ένα σύστημα σωματιδίων ιδανικού αερίου σε σταθερή θερμοκρασία, όγκο και αριθμό σωματιδίων που διέρχεται από διάφορες καταστάσεις j (j=1,2,3,...) και η συνολική Ενέργεια είναι Εj . Θεωρούμε τις καταστάσεις κβαντικές δηλαδή πρόκειται για διακριτές τιμές. Τότε το στατιστικό άθροισμα είναι ένα κανονικό στατιστικό άθροισμα και δίνεται από τον τύπο:

$Z=\sum _{j}e^{-\beta E_{j}},$

Στην περίπτωση που έχουμε συνεχή κατανομή θεωρούμε σύστημα σωματιδίων φυσικού αερίου όπου οι ενέργειες των μικροκαταστάσεων είναι πολύ κοντά και η κατανομή των ενεργειών Ει θεωρείται συνεχής. Το στατιστικό άθροισμα δίναιται με ολοκλήρωμα

$Z={\frac {1}{N!h^{3N}}}\int \exp[-\beta H(p_{1},\ldots ,p_{N},x_{1},\ldots ,x_{N})]\,d^{3}p_{1}\ldots d^{3}p_{N}\,d^{3}x_{1}\ldots d^{3}x_{N},$

Η διασπορά

Είναι το μέτρο που περιγράφει την μεταβλητότητα ή την ανομοιογένεια των παρατηρήσεων σε ένα σύνολο δεδομένων. Όσο μεγαλύτερη είναι η διασπορά τόσο λιγότερο αντιπροσωπευτική είναι η μέση τιμή

Τα μέτρα της διασποράς είναι η διακύμανση, η τυπική απόκλιση, το εύρος και το τετραμοριακό εύρος

Η και η τυπική απόκλιση της κατανομής σ

Σαν απόκλιση λέμε την διαφορά οποιασδήποτε τιμής από την μέση τιμή

Η τυπική απόκλιση μετρά τη διακύμανση ή την μεταβλητότητα σε ένα σύνολο σημείων γύρω από έναν μέσο όρο και αποτελεί το μέτρο της διασποράς των τιμών τυχαίων μεταβλητών αναμενόμενη τιμή ( μέση τιμή -μαθηματική προσδοκία) Ερμηνεύουμε τα δεδομένα γύρω από τη μεταβλητότητά τους. Μικρή τυπική απόκλιση σημαίνει ότι τα σημεία δομένων είναι συγκεντρωμένα γύρω από τον μέσο όρο.

Δίνεται από τον τύπο $\sigma ={\sqrt {D[X]}}$ .

Διακύμανση δείγματος σ²

Η εκτίμηση της τυπικής απόκλισης αναφέρεται μερικές φορές ως διακλυμανση δείγματος $S={\sqrt {{\frac {1}{n}}\sum _{i=1}^{n}\left(x_{i}-{\bar {x}}\right)^{2}}}$

Το στατιστικό βάρος w ( Γ, g, w, W, ή Ω )

Χρησιμοποιείται στη κβαντική μηχανική και τη κβαντική στατιστική και καθορίζει τον αριθμό των διαφορετικών κβαντικών καταστάσεων με την ίδια ενέργεια. Συμβολίζεται με τα γράμματα: Γ, g, w, W, ή Ω . Είναι αδιάστατος ακέραιος αριθμός μεγελύτερος ή ίσος του ένα w>1 'η w=1.

Οι Στατιστικές Συλλογές

Συλλογή δημιουργούν - αποτελούν συστήματα που αποτελούνται από το ίδιο μεγάλο πλήθος πανομοιότυπων συστημάτων. Τα συστήματα έχουν τα ίδια μακτοσκοπικά χαρακτηριστικά (T, P, V, N) αλλά στα μικροσκοπικά διαφέρουν μεταξύ τους.

Οι σχέσεις τους με τα διπλανά Ν-1 περιβάλλοντα υποσυστήματα: Τα υποσυστήματα μπορούν ή δεν μπορούν να ανταλλάσουν ενέργεια και μάζα. Ανάλογα κατατάσσονται σε:

ΜΙΚΡΟΚΑΝΟΝΙΚΗ ΣΥΛΛΟΓΗ: Πολύ μεγάλο πλήθος από πανομοιότυπα συστήματα απομονωμένα

ΚΑΝΟΝΙΚΗ ΣΥΛΛΟΓΗ: Πολύ μεγάλο πλήθος πανομοιότυπων συστημάτων που ανταλλάσουν ενέργεια

ΜΕΓΑΛΟΚΑΝΟΝΙΚΗ ΣΥΛΛΟΓΗ: Πολύ μεγάλο πλήθος από πανομοιότυπα συστήματα που ανταλλάσουν με το ιδια και ενέργεια και σωματίδια

Η ΚΑΤΑΝΟΜΗ ΠΙΘΑΝΟΤΗΤΩΝ

Η κατανομή πιθανοτήτων περιγράφει το εύρος των τιμών μιας τυχαίας μεταβλητής και τις αντίστοιχες πιθανότητες εμφάνισης αυτών των τιμών. Περιγράφει πως οι πιθανότητες μιας τυχαίας μεταβλητής κατανέμονται στις πιθανές τιμές της. Εκχωρεί μια πιθανότητα σε κάθε πιθανή τιμή μιας τυχαίας μεταβλητής

Υπάρχουν δύο κύριοι τύποι κατανομών η διακριτή και η συνεχής

Διακριτές και οι συνεχείς κατανομές

Ένας βασικός διαχωρισμός των κατανομών είναι οι διακριτές και οι συνεχείς κατανομές

Μια διακριτή κατανομή χρησιμοποιεί μεμονωμένες τιμές από ένα διάστημα {α, β } και χωρίζει τα δεδομένα σε κατηγορίες (υποδιαστήματα)

Διακριτές κατανομές είναι 1. Η διακριτή ομοιόμορφη κατανομή 2. Η διονυμική κατανομή 3. Η υπεργεωμετρική κατανομή 4. η κατανομή Poisson

Μια συνεχής κατανομή λαμβάνει οποιαδήποτε τιμή μεταξύ δύο μεμονωμένων τιμών σε ένα διάστημα {α, β}. Εάν έχουμε μεγάλο αριθμό παρατηρήσεων από δεδομένα με συνεχείς τιμές, μπορούμε να μικρύνουμε σημαντικά το εύρος των υποδιαστημάτων ώστε από την διακριτή κατανομή να φτιάξουμε μια συνεχή

Συνεχείς κατανομές είναι: 1. η συνεχής ομοιόμορφη κατανομή 2. η εκθετική κατανομή 3. οι Γάμμα και βήτα κατανομές 4. η κανονική κατανομή

Τον τρόπο που περνά ο ένας τύπος κατανομής (διακριτή) στον άλλο (συνεχής) δείχνει η εξέλιξη της κατανομής Poisson (διακριτή) στην κανονική κατανομή (ή Γκαουσιανή) που είναι συνεχής για πιο εξιδικευμένη μελέτη

synset.com/phys/all/ru/stat_Stat_Method.html

Παράδειγμα 1 από διακριτή κατανομή

Η συνεχής ομοιόμορφη κατανομή

n=5, где n=b-a+1.

Είναι μια διακριτή κατανομή που περιγράφει το αποτέλεσμα μιας ομοιόμορφης δειγματοληψίας ενός τυχαίου αριθμού από το σύνολο {α, α=1, ...β} όπου ο κάθε ένας αριθμός Χ ανήκει σε ένα σύνολο αριθμών και έχει ίδια πιθανότητα να επιλεγεί Ρ(Χ=xi)= 1 /n

Παράδειγμα 2 από διακριτή κατανομή

Η κατανομή Poisson

Παραδείγματα της κατανομής Πουασσόν με $\lambda =1,4,10$ .

Εκφράζει την πιθανότητα ένας δεδομένος αριθμός γεγονότων να συμβαίνουν σε ένα σταθερό διάστημα χρόνου ή και χώρου (όπως με σταθερό ρυθμό ή σε μια συγκεκριμένη επιφάνεις ή χώρο). Έχει περάμετρο λ που δηλώνει την μέση τιμή του αριθμού των γεγονότων ανεξάρτητα της στιγμής Η τιμή της είναι $P_{\lambda }(X=k)={\frac {\lambda ^{k}}{k!}}\,\mathrm {e} ^{-\lambda }$

Παράδειγμα από συνεχή κατανομή

Κανονική κατανομή ή κατανομή Gaussian

Η κανονική κατανομή είναι μια συνεχής κατανομή πιθανότητας με κορυφη στο κέντρο έχει μέση τιμή 0 (μ=0) και τυπική απόκλιση 1 (σ=1) και συμβολίζεται Ν(0,1) . Η συγκεκριμένη λέγεται και τυπική κανονική κατανομή.

Επίνοήθηκε από τον Gauss και χρησιμοποιείται για να περιγράψει μεγέθη που είναι συγκεντρωμένα γύρω από μια μέση τιμή

Στην μονοδιάστατη περίπτωση δίνεται από την

συνάρτηση Gauss

$f(x)={\frac {1}{{\sqrt {2\pi }}\sigma }}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}$ , όπου μ =αναμενόμενη τιμή, μέσος όρος, σ η τυπική απόκλιση, σ² η διακύμανση της κατανομής.

Η εκθετική κατανομή

Ο μέσος όρος δίνεται από τη σχέση $\mathrm {E} [X]={\frac {1}{\lambda }}.\!$

Άλλες στατιστικές κατανομές που χρησιμοποιούντα.ι

Αθροιστική συνάρτηση κατανομής (CDF)

Χρησιμοποιείται για να μετρήσει την πιθανότητα μιας τυχαίας μεταβλητής να παίρνει τιμές σε ένα διάστημα. Είναι αύξουσα και δεξιά συνεχής

Μεθοδολογία των Επιστημών του Ανθρώπου: Στατιστική Ενότητα 1 ... Αθροιστική Συνάρτηση Κατανομής για διακριτές κατανομές

.Συνάρτηση κατανομής: Είναι μια συνάρτηση που χαρακτηρίζει την κατανομή μιας τυχαίας μεταβλητής ή διανύσματος. Μπορώ να περιγράψω το μέτρο κατανομής χρησιμοποιώντας την αθροιστική συνάρτηση κατανομής η οποία ορίζεται

για διακριτές μκατανοές

$F(x)=\operatorname {P} (X\leq x)=\sum _{x_{i}\leq x}\operatorname {P} (X=x_{i})=\sum _{x_{i}\leq x}p(x_{i}).$

Αθροιστική Συνάρτηση Κατανομής για συνεχείς κατανομές

$F(x)=\operatorname {P} (X\leq x)=\int _{-\infty }^{x}f(t)\,\operatorname {d} t$

Η Αθροιστική συνάρτηση κατανομής δίνεται από τον τύπο

$F(x;\lambda )={\begin{cases}1-e^{-\lambda x},&x\geq 0,\\0,&x<0.\end{cases}}$

ή εναλλακτικά από:

$F(x;\lambda )=\mathrm {(} 1-e^{-\lambda x})H(x)\!$

Η συνάρτηση πυκνότητας πιθανότητας

Αναφέρεται σε συνεχείς κατανομές

Είναι η συνάρτηση κατανομής ή πλήρης συνάρτηση στατιστικής κατανομής (σε χρονική στιγμή t, αριθμού σωματιδίων qi, τιμών πιθανοτήτων q_i ),

που είναι μια πυκνότητα σημείων απεικόνισης στον χώρο των φάσεων.

Οπότε, το σύνολο τιμών πιθανοτήτων q_i δίνεται ως εξής:

Η συνάρτηση πυκνότητας πιθανότητας μιας εκθετικής κατανομής είναι η:

$f(x;\lambda )={\begin{cases}\lambda e^{-\lambda x},&x\geq 0,\\0,&x<0.\end{cases}}$

Συνάρτηση πυκνότητας πιθανότητας

αλλά δίνεται και έτσι

$f(x;\lambda )=\mathrm {\lambda } e^{-\lambda x}H(x)\!$

ορίζεται στο διάστημα [0, ∞).

Η πιθανότητα εύρεσης ενός συστήματος σε ένα στοιχείο χώρου φάσεων dqdp που είναι $\mathrm {d} q\,\mathrm {d} p\equiv \prod \limits _{i}\mathrm {d} q_{i}\,\mathrm {d} p_{i}$

δίνεται από τον τύπο: dω= ρ(t, q, p)dqdp

$\int {\rho \!\left(t,q,p\right)\,\mathrm {d} q\,\mathrm {d} p}=1,\qquad (2)$

Συνάρτηση κανονικής πυκνότητας κατανομής πιθανότητας f(z) PDF

Περιγράφει την πιθανότητα μιας συνεχούς τυχαίας μεταβλητής να πάρει μια συγκεκριμένη τιμή. Η συνάρτηση είναι μη αρνητική f(x) >0 ή f(x) = 0 και η ολική πιθανότητα σε όλο το πεδίο ορισμού πρέπει να είναι 1.

Παραδείγματα

Η συνάρτηση κανονικής πυκνότητας κατανομής ονομάζεται και κατανομή καμπάνας γιατί έχει σχήμα που μοιάζει με καμπάνα

Η συνάρτηση πικνότητας πιθανότητας δίνεται από

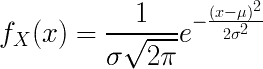
$f_ {X} (x) = \ frac {1} {\ sigma \ sqrt {2 \ pi}} e ^ {- \ frac {(x- \ mu) ^ 2} {2 \ sigma ^ 2}}$

Η συνάρτηση πυκνότητας πιθανότητας στην εκθετική κατανομή είναι:

$f(x;\lambda )=\mathrm {\lambda } e^{-\lambda x}H(x)\!$ και ορίζεται στο διάστημα ( 0, άπειρο) και λ>0

ΚΑΤΑΝΟΜΕΣ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΕΙΤΑΙ Η ΕΚΘΕΤΙΚΗ ΣΥΝΑΡΤΗΣΗ

Στις κατανομές αυτές πρέπει επίσης να έχουμε υπ' όψην μας και κάποια άλλα στοιχεία όπως:

Η διάμεσος του Χ δίνεται από τον τύπο

Εάν το σ πολλαπλασιάζεται με έναν συντελεστή έως το σ τότε η πυκνότητα πιθανότητας πρέπει να κανονικοποιηθεί

Μια κανονική κατανομή με q και p να διαφέρουν από την τυπική,

Η ΣΥΝΑΡΤΗΣΗ ΕΠΙΜΕΡΙΣΜΟΥ

Η συνάρτηση επιμερισμού χρησιμοποιείται για την κανονικοποίηση της συνάρτησης πιθανότητας στην περίπτωση που το άθροισμα των επιμέρους πιθανοτήτων είναι διαφορετικό από την μονάδα. Η εισαγωγή της συνάρτησης επιμερισμού εξασφαλίζει αυτην την συνθήκη.

Στη στατιστική μηχανική η συνολική ενέργεια ενός συστήματος δίνεται από τον τύπο $\ E=\sum _{j}E_{j}P_{j}$ .