Οι Φυσικές Επιστήμες στις αρχές του 21ου αιώνα. Μέρος Δεύτερο: Σύζευξη και Υπέρθεση και διαχωρισμός της κυματοσυνάρτησης. Θεώρημα Fourier. Συμβολόμετρα σωματιδίων. Αποσυνοχή.

της Δήμητρας Σπανού καθηγήτριας Χημικού 

Η μνήμη, η προφητεία και η φαντασία - το παρελθόν, 

το μέλλον και η ονειρική στιγμή που 

μεσολαβεί- είναι όλα μια χώρα που ζει μια

και μοναδική αθάνατη μέρα.

Να το ξέρεις αυτό είναι Σοφία.

Να το χρησιμοποιείς είναι η Τέχνη

έτσι ξεκινά το βιβλίο του Clive Barker "Το μεγάλο μυστικό Θέαμα"

..οπως αναφέραμε στο πρώτο μέρος  πολλές είναι οι θεωρήσεις και οι πειρα  που μαρτυρούν τον  κυματοσωματικό δυισμο 

Στο δεύτερο μέρος  θα δούμε να εφαρμόζονται περιπτώσεις του κβαντικού εναγκαλισμού

Κβαντωση φυσικών μεγεθών σε φερμιόνια . (Ηλεκτρόνια ατόμου)

Έχουμε  αναφέρει για τους δυο τύπους σωματιδίων τα φερμιόνια ( φορείς ύλης και τα μποζόνια (φορείς ενέργεις)

Ακόμα  γνωρίζουμε ότι πολλά φυσικά μεγάθη χαρακτηρίζονται από κβάντωση των ποσοτήτων τους, που παίρνουν συγκεκριμένες τιμές , πολλαπλάσιες μιας στοιχειώδους ποσότητας του εκάστοτε φυσικού μεγέθους. 

' Κατά την κατασκευή των ατόμων της ύλης  με την τοποθέτηση ηλεκτρονίων γύρω από τον πυρήνα έχουμε κβάντωση σε φυσικά μεγέθη 

α.με τον ορισμό επιτρεπόμενων τροχαιών  (κβάντωση της απόστασης από τον θετικό πυρήνα άρα κβάντωση και στην ενέργεια)

  η=1,2,3,...

 β. με την κβάντωση στο μέτρο της στροφορμής των ηλεκτρονίων που περιστρέφονται γύρω από τον πυρήνα

 l=0,1,2,...,n-1

γ. κατά την περιστροφή των ηλεκτρονίων γύρω από τον εαυτό τους   ο προσανατολισμού του ηλεκτρονικού νέφους σε σχέση με τους άξονες x, y, z της περιστροφής του ηλεκτρονίου γύρω από τον εαυτό του (SPIN)

Κβάντωση στις συνιστώσες της στροφορμής SPIN  ml= -l, (-l+ 1), …, 0,…1, (l-1), +l

δ. Κβάντωσν κατά τον προσανατολισμό της  ιδιοπεριστροφής του ηλεκτρονίου (spin).  m_s = +1/2, και m_s = -1/2,

Για τους αριθμούς αυτούς ισχύει η απαγορευτική αρχή του Παουλι ( Pauli) που απαγορεύει σε ένα σωματίδιο (λ.χ. ηλεκτρόνιο που λαμβάνει μέρος στον σχηματισμό της ύλης -ατόμου) να έχει όλους τους κβαντικούς αριθμούς ίδιους με ένα άλλο δεύτερο ηλεκτρόνιο του ίδιου ατόμου .

Είναι υψηλά μαθηματική έννοια, σχετίζεται με την συμμετρία και την αντισυμμετρία των επιτρεπτών κυματοσυναρτήσεων και γενικευμένα λέει ότι

Δύο ταυτόσημα φερμιόνια δεν είναι δυνατόν να εποικίσουν την ίδια κβαντική κατάσταση

Η αρχή όμως αυτή δεν ισχύει για τα μποζόνια δηλαδή τα δυνητικά σωματίδια που είναι οι μεταφορείς ενέργειας μεταξύ των φερμιονίων (ηλεκτρόνιο, πρωτόνιο νετρόνιο που είναι απαρτίζουν το παρατηρήσιμο υλικό σύμπαν) 

Στην ίδια κβαντική κατάσταση μπορούν να κατοικούν ταυτόχρονα πολλά μποζόνια και μάλιστα το επιδιώκουν τα μποζόνια, γιατί με αυτό τον τρόπο ενισχύονται οι ιδιότητές τους

Έτσι η κυματική υπόσταση καθενός φωτονίου (μποζόνιο ορατού) μπορεί να τονώσει τις κυματικές ιδιότητες άλλων όμοιων φωτονίων και να δημιουργήσει ένα μακροσκοπικό κυματικό φαινόμενο (σύζευξη και υπέρθεση κυμάτων)

Αυτό όμως δεν επιτρέπεται σε φερμιόνια που συνθέτουν την συνηθισμένη ύλη όπου βέβαια υπάρχει η μεταξύ τους αλληλοεξάρτηση και ισχύει η απαγορευτική αρχή του  Pauli

Εάν όμως  έχουμε ένα απομονωμένο σωματίδιο

Τότε μπορούν  να υπεισέλθουν πάλι οι κυματικές ιδιότητες 

Α. στο πείραμα των δυο σχισμών,

Ένας τρόπος για να ανιχνεύσουμε το φως ή την ύλη είναι η μέθοδος των σχισμών συγκρίσιμου μεγάθους, από τις οποίες διέρχεται ηλεκτρομαγνητική ακτινοβολία (λ.χ. φωτόνια) ή σωματίδια (π.χ. ηλεκτρόνια). Αυτά καταλήγουν ένα πέτασμα ή μια οθόνη ανίχευσης που υπάρχει πίσω.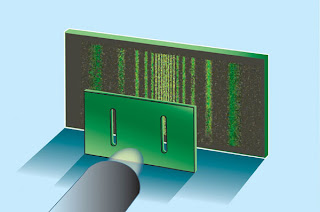

 Αν τα φωτόνια, πριν πέσουν στην οθόνη ανίχνευσης, διέλθουν από μια λεπτή σχισμή που έχει πάχος συγκρίσιμο με το μήκος κύματός  τους, τότε αποτυπώνεται στην οθόνη το σχήμα του φαινομένου της περίθλασης

Η ερμηνεία γι αυτό είναι ότι η κάθε σχισμή από την οποία διέρχεται ένα κύμα γίνεται νέα πηγή κύματος. 

Εαν διέλθουν από ένα σύστημα με δύο, το ίδιο κοντινές, παράλληλες τέτοιες σχισμές,   εμφανίζεται το κυματικό φαινόμενο της συμβολής.

Αυτό δείχνει ότι φωτόνια 'εχουν διέλθει και από τις δυο σχισμές. Αυτά συμβάλουν κατά την έξοδό τους

 Η εικόνα της συμβολής, με φωτεινές και σκοτεινές περιοχές στο φως αποδεικνύει την κυματική φύση του φωτός.

Παρόμοια αποτελέσματα θα έχουμε, αν από τις σχισμές περάσουν σωματίδια ύλης εφόσον το πλάτος των σχισμών είναι της ίδιας τάξης μεγέθους με τα σωματίδια (Θεωρείται επίσης ότι η ύλη εμφανίζει επίσης κυματική συμπεριφορά)

Το πείραμα των δυα σχισμών έγινε το 1950 με ηλεκτρόνια, το 1970 το ίδιο πείραμα επανήφθηκε αλλά αντί για ηλεκτρόνια είχαμε νετρόνια με τα ίδια αποτελέσματα. Το 1980 έγινε το ίδιο με άτομα. Σε όλα παρατηρήθηκαν φαινόμενα συμβολής.

Στις τελευταίες δεκαετίες , το 1991 το ίδιο πείραμα επαναλήφθηκε με συσσωματώματα μορίων από τον Αντον Ζιλιγκερ.  Συγκεκριμένα συσσωματώματα 60 έως 70 ατόμων άνθρακα μέσα από τις δυο σχισμές έδωσαν ίδια αποτελέσματα σε μια προσπάθεια να διευρυνθούν τα πειράματα και οι αποδείξεις των κβαντικών φαινομένων για οντότοτες που δεν σχετίζονται με τον κόσμο  των πολύ μικρών διαστάσεων. 

Β. Κύματα μηχανικά, ηλεκτρομαγνητικά, κβαντικά σωματίδια

Στα μηχανικά κύματα  μεταβάλλεαι η θέση των σημείων του μέσου, που ταλαντώνονται γύρω από την θέση ισορροπίας. . Η εξίσωση κύματος για τα μηχανικά κύματα, δίνει για κάθε χρονική στιγμή την θέση κάθε σημείου του υλικού μέσου μέσα στο οποίο διαδίδεται το κύμα 

ενώ στα ηλεκτρομαγνητικά κύματα μεταβάλλεται διαρκώς η ένταση του ηλεκτρικού και του μαγνητικού πεδίου. Η τιμή της έντασης του ηλεκτρικού και του μαγνητικού πεδίου σε σχέση με την απόσταση και τον χρόνο δίνεται από τις εξισώσεις του ηλεκτρομαγνητικού κύματος

Στα κβαντικά σωματίδια η κβαντομηχανική με την εξίσωση Στρόντιγκερ που περιγράφει ένα σωματίδιο-κύμα, 

δεν σχετίζεται με κάποιο μέσο διάδοσης όπως α μηχανικά ούτε με κάποιες ιδιότητες του χώρου σχετίζεται και περιγράφει φυσικά φαινόμενα όπως τα ηλεκτρομαγνητικά, 

 Η κυματοσυνάρτηση δεν περιγράφει μόνο το σωματίδιο-κυμα αλλά και την επιρροή του η οποία εξαπλώνεται στον χώρο και στον χρόνο

 Η εξίσωση Στρέντιγκερ Εκτείνεται σε όλον τον χώρο χωρίς να είναι κυματοσυνάρτηση και αποδίδει :

Για κάποιο συγκεκριμένο σημείο σε κάποια χρονική στιγμή η κυματοσυνάρτηση (η οποία σημειωτέον έχει και μιγαδική παράμετρο) δίνει συγκεκριμένη τιμή.  

1. Πως η κυματοσυνάρτηση μεταβάλλεται στον χώρο, (πρώτος όρος στο πρώτο μέλος, 

2. Τις δυνάμεις που δρουν στο σωματίδιο-κύμα (δεύτερος όρος πρώτου μέλους) και 

3. Πως αλλάζει το σχήμα Ψ με τον χρόνο.

4.Το σύμβολο Ψ αντιπροσωπεύει το κύμα του ντε Μμπρογλί.

Όσον αφορά την αβεβαιότητα στην θέση του αποδεικνύεται, εφ όσον δεχόμαστε  ότι το σωματίδιο δεν είναι τίποτε άλλο από ένα κυματοπακέτο που διαστέλλεται στον χώρο. Την απροσδιοριστία στην ορμή  γιατί απλώνεται και στον χρόνο

Εφόσον το κυματοπακέτο αυτό αποτελείται από ένα μείγμα κυμάτων  με διαφορετικά μήκη κύματος που διαδίδονται με διαφορετικές ταχύτητες το πακέτο είναι φυσικό να εξαπλωθεί

Ακόμα με την εξίσωση αυτή η αρχική προσέγγιση που εισάγει την "ενοχλητική " έννοια του κβαντικού άλματος (της πρώιμης περιόδου της κβαντικής θεωρίας), ξεπεράστηκε με την εισαγωγή μιας ομαλά μεταβαλλόμενης κυματομορφής

Οι αντιρρήσεις που εκφράστηκαν και από τον Αινστάιν παλαιότερα, αλλά και από άλλους  μεταγενέστερους Φυσικούς  είναι, ότι χρησιμοποιείται η στατιστική θεωρία για περιγραφή μεμονωμένων γεγονότων. Ίσως όμως ενοχλεί περισσότερο και η αβεβαιότητα και ως προς την θέση του σωματιδίου και ως προς την ορμή. Και είναι δύσκολο να θεωρήσουμε απομονωμένο οποιοδήποτε γεγονός στο σύμπαν.

Προσέχουμε επίσης πώς  σε κάθε σημείο του χώρου αποδίδονται στην συνάρτηση δύο αριθμοί.

Παρ όλα αυτά  εξίσωση Στρέντιγκερ έχει εφαρμοστεί με μεγάλη επιτυχία σε αρκετές περιπτώσεις στην κβαντική φυσική. 

Κάθε φυσικός μπορεί να εφαρμόσει την εξίσωση σε κάποια συγκεκριμένη περίπτωση,  (για παράδειγμα για να περιγράφει ένα αντικείμενο τοποθετημένο μέσα σε ένα κουτί, ή ένα ηλεκτρόνιο τοποθετημένο σε ένα δυναμικό πεδίο, ή το άτομο του υδρογόνου)

Γ. Πως αλληλοεπιρεάζονται τα σωματίδια, τα κύματα και τα κβαντικά σωματίδια

Σύγκρουση σωμάτων

Ισχύει η αρχή διατήρησης της ορμής και της  ενέργειας (για την ελαστική κρουση) Συνήθως όμως έχουμε απώλειες ενέργειας με την μορφή θερμότητας (ανελαστική, πλαστική)

Κρούση δυο σωμάτων στην ίδια κατεύθυνση και σε διαφορετικές κατευθύνσεις

Κρούση με σώμα ακίνητο

πλαστική κρούση

Συνάντηση  κυμάτων 

Τα κύματα αλληλοεπηρεάζονται και σε ορισμένες περιπτώσεις  δυο συνθέτουν ένα νέο κύμα

Όταν δυο παλμοί (κύματα μικρής διάρκειας) συναντιώνται περνούν ο ένας μέσα από τον άλλο και χωρίς κανένας τους να αλλοιωθεί και αυτό είναι μια θεμελιώδης ιδιότητα των κυμάτων

Τα κύματα καθώς διασταυρώνονται όμως, συνδυάζονται και δίνουν ανάλογα σχήματα. Στα σημεία συνάντησης συμβαίνει υπέρθεση

Υπέρθεση κυμάτων: Η µετατόπιση σε οποιοδήποτε σηµείο προκύπτει από το διανυσµατικό άθροισµα όλων των κυµάτων που διέρχονται από το συγκεκριµένο σηµείο σε κάθε χρονική στιγµή (αρχή της επαλληλίας).

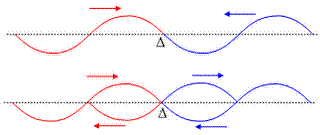
Μπορεί να συναντηθούν κύματα διαφορετικών κατευθύνσεων

Σε κύματα ισα αντίθετα και συμμετρικά στην 

ίδια ευθεία έχουμε το φαινόμενο του στάσιμου κύματος. Για ορισμένες βασικές περιπτώσεις υπάρχουν μαθηματικοί υπολογισμοί και ανάλογες εξισώσεις

 Στα μηχανικά κύματα

Σύνθεση δύο απλών αρμονικών ταλαντώσεων μηχανικών κυμάτων της ίδιας συχνότητας

x=A₁ημωt+A₂ημ(ωt+φ)   

 Στα ηλεκτρομαγνητικά κύματα 

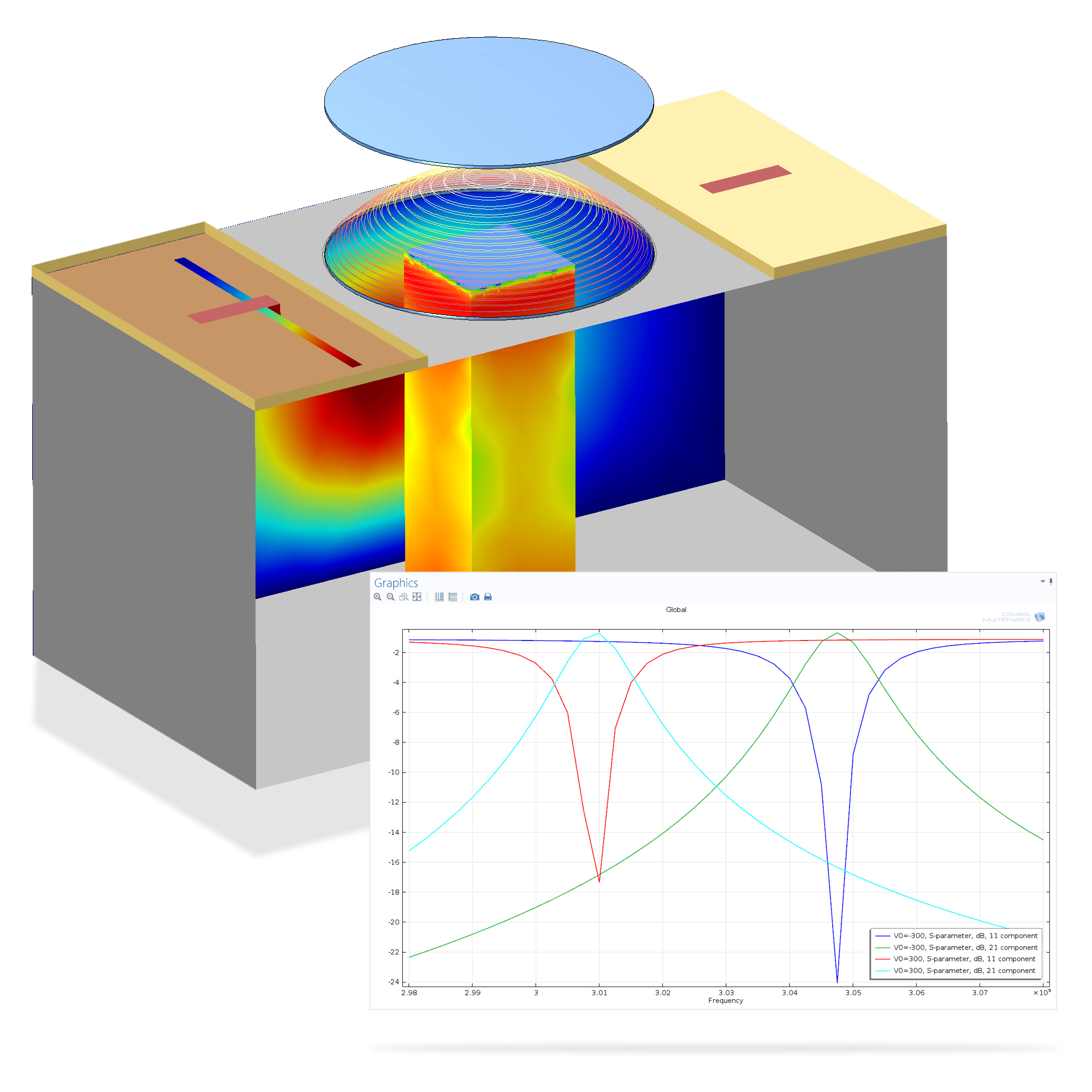
Κβαντική σύζευξη κυμάτων . Υπέρθεση κβαντικού σωματιδίου

Υπέρθεση  κβαντικού σωματιδίου: Ένα κβαντικό σωματίδιο μπορεί να υφίσταται σε έναν συνδυασμό δυο ή περισσότερων καταστάσεων την ίδια χρονική στιγμή. Η νέα κατάσταση αντικαθιστά τις προηγούμενες. Λόγω της δυσκολίας στους υπολογισμούς χρησιμοποιούνται τα  μαθηματικά με τους  μετασχηματισμούς των σειρών Fourier ώστε να συμπεριλάβουν μιγαδικές μεταβλητές που συναντάμε στις κβαντικές εξισώσεις

Στην Χημεία η έννοια του τροχιακού (κλασσική περίπτωση κυματοσυνάρτησης) έχει κληρονομηθεί από την παλιά Κβαντική Θεωρία’ του Bohr . Κατά την κατασκευή των ατόμων και τον σχηματισμό χημικών δεσμών μεταξύ τους εφαρμόζεται η υπέρθεση των  κυματοσυναρτήσεων των τροχιακών και η δημιουργία νέων τροποποιημένων συναρτήσεων-τροχιακών που είναι το αποτέλεσμα της σύζευξής τους

Ενώ βέβαια τα ατομικά τροχιακά τίποτε άλλο δεν είναι παρά οι επιλύσεις της εξίσωσης Στρέντιγκερ

 Η Ιστορία των Φυσικών Επιστημών. Μέρος Έβδομο: Πέρα από την Κλασσική Φυσική ΙΙ. Η Κβάντωση των Φυσικών μεγεθών: Η Ερμηνεία των κβαντικών φαινομένων από "σκληρά" Μαθηματικά

Στον κόσμο της Χημείας διεισδύει ο κόσμος της κβαντικής φυσικής που βέβαια πολλοί χημικοί αποφεύγουν να το παίρνουν υπ΄όψην τους γιατί μοιάζει να βρίσκεται έξω από το αντικείμενό τους .  Βέβαια σε βάθη που τα όρια ενέργειας και υλικής υπόστασης του κόσμου έχουν γίνει ασαφή, είναι δύσκολο να μιλάμε για ειδικά αντικείμενα 

Έχοντας αυτά υπ όψην μας αναφέρουμε κάποια πειράματα στην συνέχεια που επεκτείνουν τα προηγούμενα αλλά και ανοίγουν νέους ορίζοντες

Δ. Υπέρθεση σε μικροσκπικά και σε μακροσκοπικά αντικείμενα  

Η υπέρθεση ανικειμένων ευνοείται κυρίως σε μικροσκοπικά αντικείμενα και σε απομόνωση από το περιβάλλον

 Έτσι, τα μικροσκοπικά αντικείμενα γενικά απομονώνονται πιο εύκολα και διατηρούν περισσότερο την κβαντική τους συμπεριφορά. 

Εάν σύστημά μας βρίσκεται σε μια τέτοια υπέρθεση,  αν δεν μεσολαβήσει κάποια αλληλεπίδραση του συστήματος με το περιβάλλον, το σύστημα θα εξακολουθήσει να βρίσκεται σ' αυτή την υπέρθεση. 

Βρέθηκε  ότι οι σύμφωνες κβαντικές υπερθέσεις διαρκούν μόνο όσο παραμένουν "μυστικές" και απομονωμένες από το υπόλοιπο του κόσμου. (Wojciech Zurek, Zeh ) 

Στα μέχρι τώρα πειράματα  με μεγάλη προσπάθεια, μόνο μικροσκοπικά αντικείμενα  (όπως το τραμπουλόχαρτο είναι δύσκολο να βρεθούν σε υπέρθεση  με σημαντικές εξαιρέσεις 

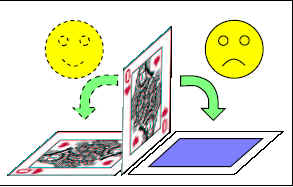
Στο τραπουλόχαρτο (που είναι μακροσκοπικό και μη απομονωμένο αντικείμενο), που ισορροπεί στην κόψη του βρίσκεται σε μια υπέρθεση δύο καταστάσεων. Μιας που φαίνεται η φιγούρα του τραπουλόχαρτου και μιας που είναι η πίσω όψη του (με μπλε χρώμα στην εικόνα.)

Οι επιδράσεις από το περιβάλλον (αέρας, φωτόνια κ.λ.π.)  θα οδηγήσει εύκολα την κυματοσυνάρτηση της υπέρθεσης, σε κατάρευση

Η χρησιμότητα των μαθηματικών σειρών Fourier για κατανόηση και υπολογισμούς στην κυματική

Στους υπολογισμούς της κβαντομηχανικής, χρησιμοποιούνται οι μαθηματικές σειρές Fourier. Αυτές  προέκυψαν από την προσπάθεια κατανόησης των ιδιοτήτων  μιας συνάρτησης (η οποία μπορεί να αναπαριστά ένα σήμα) μέσω της αποσύνθεσής της  (διάσπασής της σε γνωστά στοιχειώδη μέρη )

Ισχύει και η ανάστροφη διαδικασία που ονομάζεται σύνθεση , που χρησιμοποιούμε τις ίδιες μαθηματικές σειρές

Στους μετασχηματισμούς έχουμε μια διαδικασία που αποσυνθέτει μία συνάρτηση σε άθροισμα απείρων περιοδικών ημιτονοειδών και συνημιτονοειδών συναρτήσεων.

Για καθεμία από αυτές τις διεργασίες υπάρχει και ο αντίστροφος μετασχηματισμός, ο οποίος δέχεται ως είσοδο το φάσμα και δίνει ως έξοδο την αρχική συνάρτηση f. 

Οι σειρές μπορεί να μετασχηματιστούν ανάλογα έτσι ώστε να συμπεριλάβουν διάφορα πεδία της φυσικής και να δώσουν υπολογισμούς

Θεώρηµα Fourier: Κάθε σύνθετο περιοδικό κύµα µπορεί να γραφτεί ως το άθροισµα ηµιτονοειδών κυµάτων (συναρτήσεων) διαφόρων συχνοτήτων πλατών και φάσεων.

Ε. Πειράματα με ένα μοναδικό φωτόνιο ή σωματίδιο

Το πείραμα του Geoffrey Taylor

Ο φοιτητής Geoffrey Taylor μελέτησε την συμπεριφορά ενός φωτονίου που κατάφερε να απομονώσει χαμηλώνοντας την ένταση μιας μονοχρωματικής λυχνίας. Τα αποτελέσματα ήταν να καταφέρει να απομονώσει ένα μοναδικό φωτόνιο. Το ένα φωτόνιο (σωματίδιο- κύμα) έδωσε σε φωτογραφική πλάκα φαινόμενα  εικόνες περίθλασης  όμως χρειάστηκε πολύ μεγαλύτερο χρονικό διάστημα γι αυτό. 

Για το τελευταίο δηλαδή το μεγάλο χρονικό διάστημα που απαιτείται για να παρατηρηθεί το φαινόμενο μια εξήγηση μπορεί να είναι 

 πως, ο χρόνος για να συγκεντρωθεί η ενέργεια που πρέπει για να σχηματιστεί ένα φωτόνιο  είναι πολύς,  εφ όσον η ένταση της ακτινοβολίας στο πείραμα είναι η χαμηλότερη που γίνεται. 

Η ενέργεια κατά την υπέρθεση των κυμάτων (μεταφορά από Βικιπαίδεια)

Τα κύματα προκαλούνται από διαταραχές. Οι διαταραχές καταστρέφουν κάποιο είδος ισορροπίας, άρα μεταφέρουν ενέργεια, δηλαδή το κύμα μεταφέρει ενέργεια.  Η ενέργεια αυτή αξιοποιείται στη μεταβολή του διαταρασσόμενου μεγέθους, άρα και στη διάδοση του κύματος, και ένα μέρος αποθηκεύεται προσωρινά στην περιοχή διάδοσης

Συνήθως η ενέργεια που υπάρχει σε κάποια περιοχή είναι της μορφής κΑ²/2, όπου κ ένας συντελεστής που εξαρτάται από την περιοχή του μέσου και Α το πλάτος του κύματος. . Επίσης, παρατηρείται το φαινόμενο η ενέργεια να μετατρέπεται περιοδικά μεταξύ δύο διαφορετικών ειδών ενέργειας, για παράδειγμα κινητική ενέργεια, δυναμική ενέργεια στα μηχανικά κύματα ή ηλεκτρική δυναμική ενέργεια και μαγνητική δυναμική ενέργεια στα ηλεκτρομαγνητικά κύματα.

Η ανά μονάδα επιφάνειας ενέργεια χαρακτηρίζει όλες τις περιοχές της συγκεκριμένης σφαίρας, και ονομάζεται ένταση. Η ένταση του φωτός θεωρείται θεμελιώδες μέγεθος και μετριέται σε κηρία (ή καντέλες) cd. (https://el.wikipedia.org/wiki/Κύμα)

 Το πλάτος του κύματος σε ένα σημείο έχει άμεση σχέση με την ενέργεια του κύματος σε αυτό το σημείο.

υπ όψη ότι το φωτόνιο σχηματίζεται μετά από διέλευση αρκετών κυμάτων στο μεγάλο χρονικό διάστημα που θα αθροίσουν αρκετή ενέργεια αρκετή για τον σχηματισμό ενός  φωτονίου δηλαδή ενός μακροσκοπικού φαινόμενου.

Πρακτικά αυτό δείχνει ότι η κυματοσυνάρτηση του φωτονίου έχει διασπαστεί σε άλλες σύμφωνα με τα παραπάνω.

Αντίστοιχο πείραμα από τον John King με ένα φωτόνιο και δυο σχισμές

Αντίστοιχο πείραμα από τον John King όπου ένα φωτόνιο περνά από μια και από δύο σχισμές ταυτόχρονα πράγμα που δεν συμβαδίζει με την επικρατούσα λογική της καθορισμένης τροχαιάς των φωτονίων και των σωματιδίων. 

Η κβαντική αλήθεια είναι πως η κίνησή τους περιγράφεται από ένα κύμα που μπορεί να περάσει ταυτόχρονα και από τις δυο σχισμές.

Αντίστοιχα αποτελέσματα με την εκπομπή ενός σωματιδίου

Ακόμα ποιο εντυπωσιακό γίνεται το πείραμα όταν ξεκινάει αρχικά με την εκπομπή σωματιδίου . 

Μεμονωμένο σωματίδιο διέρχεται από δυο σχισμές

Θυμόμαστε ότι 

Εάν   έχουμε ένα απομονωμένο σωματίδιο

Τότε μπορούν  να υπεισέλθουν πάλι οι κυματικές ιδιότητες  σε αυτό

Πολύ σημαντικό πείραμα που εμφανίζει την ανεξήγητη συμπεριφορά ενός μοναδικού  σωματιδίου που κατά την διαδρομή του συναντά πέτασμα με δυο σχισμές , μετατρέπεται σε κύμα , περνά και από τις δύο σχισμές ταυτόχρονα και στην συνέχεια οι ακτινοβολίες που δημιουργούν φαινόμενα συμβολής  

Σύμφωνα με την κβαντική θεωρία κάθε σωματίδιο- κύμα δεν είναι παρά μια σειρά άλλων κυμάτων που βρίσκονται σε υπέρθεση και ακολουθούν διαφορετικές πορείες

Είναι δυνατόν στην συνέχεια να τα κύματα αυτά, να συμβάλουν και να  αποτελέσουν εκ νέου το αρχικό σωματίδιο - κύμα. 

ΠΙΘΑΝΟΝ ΝΑ ΕΙΝΑΙ ΟΛΑ ΑΠΟΤΕΛΕΣΜΑ ΤΩΝ  ΔΙΑΦΟΡΕΤΙΚΩΝ ΔΙΑΣΤΑΣΕΩΝ ΤΟΥ ΚΒΑΝΤΙΚΟΥ ΚΟΣΜΟΥ ΚΑΙ ΤΗΣ ΔΙΑΦΟΡΕΤΙΚΗΣ ΧΡΟΝΙΚΗΣ ΚΛΙΜΑΚΑΣ ΠΟΥ ΔΕΝ ΕΧΟΥΜΕ

Σταν κόσμο της κβαντικής μηχανικής η λογική  και η αντίληψή μας πρέπει να επεκταθούν  πολύ , ώστε να συμπεριλάβουν παράδοξα φαινόμενα όπως η  υπέρθεσης ή της διέλευσης του μοναχικού φωτονίου από την διπλή σχισμή ή ακόμα της ζωντανής και ταυτόχρονα νεκρής γάτας του Στρίντιγκερ. Όμως όλα αυτά μπορεί απλά να οφείλονται στις τεράσιες διαφορές των μέτρων για μεγεθών του κοσμου μας και του κόσμου των κβάντων. Την δική μας πραγματικότητα ακολουθούν βέβαια και οι αισθήσεις μας και είναι δύσκολο να διακρίνουμε φαινόμενα που τα χωρίζει ένα χρονικό διάστημα, που για μας είναι τόσο απειροελάχιστο ώστε είναι αδύνατον να αντιληφθούμε την διαφορά του πριν και του μετά. Ενα παράδειγμα για το πόσο μικρό μπορεί να είναι έν χρονικό διάστημα  αναφέρεται στο βιβλίο "Κβαντικά Παράδοξα" ως εξής:

Ο αριθμός των διαδρομών που μπορεί να κάνει ένα πρωτόνιο από το ένα άκρο του πυρήνα στο άλλο, στην διάρκεια ενός δευτερολέπτου είναι χιλιάδες φορές μεγαλύτερος από τον αριθμό των δευτερολέπτων που πέρασαν από την Μεγάλη Έκρηξη έως σήμερα!

υπό κατασκευή

Η εικόνα της Συμβολής δημιουργείται όταν οι δυο διαδρομές δεν είναι διακρίσιμες.

Η μαθηματική απόδειξη έχει ήδη δοθεί. 

Οι εξισώσεις Schrödingerκαι Heisenberg, διατυπώνονται με βάσει την διττή υπόσταση της ύλης και οι υπολογισμοί με τις σειρές Fourier δίνουν την δυναότητα να αποσυνθέσουμε μια κυματοσυνάρτηση σε άλλες που την αποτελούν αλλά και αντίστροφα να συνθέσουμε μια κυματοσυνάρτηση από άλλες απλούστερες

ΣΤ. Την πειραματική απόδειξη αυτών των φαινομένων πετυχαίνουν τα συμβαλόμετρα

Συμβολόμετρα ήχου

Συμβολόμετρα φωτονίων

Συμβολόμετρα σωματιδίων

Διατάξεις που αποδεικνύουν πως ένα μεμονωμένο σωματίδιο μπορεί να ταξιδεύει ταυτόχρονα κατά μήκος δυο διαδρομών 

Όταν οι διαδρομές συναντηθούν ξανά δείνουν εικόνες συμβολής και επανεμφανίζεται 

α) Συμβολόμετρο ήχου

Ένα ατομικό συμβολόμετρο χωρίζει ένα άτομο σε δύο κύματα, χωρικά χωρισμένα. Τα δύο μέρη του ατόμου ανασυνδέονται στη συνέχεια και μπορούν να συμβάλλουν το ένα με το άλλο. Το απλούστερο παράδειγμα ενός τέτοιου διαχωρισμού συμβαίνει όταν ρυθμίσουμε το άτομο να περνάει μέσα από δύο σχισμές που απέχουν κατά λίγο.

στην εικόνα 

β) Διαιρέτες οπτικής δέσμης

 β)Το συμβολόμετρο του Michelson. γ) Ένα σύγχρονο δ) Εικόνα κροσσών συμβολής από συμβολόμετρο ε)Το συμβολόμετρο 

του Michelson 

Η  προσπίπουσα φωτεινή δέσμη αναλύεται σε δυο που ακολουθούν διαφορεικές διαδρομές. Μπορεί να ρυθμιστεί το κάθε μήκος της διαδρομής καθώς και ο δείκτης διάθλασης και να πάρουμε διάφορα αποτελέσματα

Ίσως κάτι να θέλει να μας  πει 

Με την εξίσωση αυτή όπως έχει ειπωθεί στην αρχή, μπορούμε να εξάγουμε πληροφορίες σχετικά με την φύση 

Αυτή η εξίσωση σε κάθε στιγμή δίνει τιμή σε κάθε σημείο του χώρου. 

Είναι μιγαδική και μόνο το τετράγωνο μπορεί να έχει κάποιο φυσικό νόημα και το πιο αξιοπρόσεκτο είναι ότι, 

Σε κάθε σημείο του χώρου αποδίδονται στην συνάρτηση αυτή δύο αριθμοί

Δήμητρα Σπανού

ΠΗΓΕΣ

Φυσική Θετικής και Τεχνολογικής κατεύθυνσης Γ Λυκείου

Κβαντικά παράδοξα Jim Al Khalili

Φυσική για ποιητές Robert March

https://el.wikipedia.org/wiki/Πείραμα_των_δύο_σχισμών

www.physics4u.gr339 × 261

https://el.wikipedia.org/wiki/Συμβολή_(φυσική)

https://www.physics4u.gr/articles/laser4.html

https://ebooks.edu.gr/modules/ebook/show.php/DSGL-C108/141/1020,3650/

en.wikipedia.org300 × 160

www.comsol.com2000 × 2000

physicsgg.me565 × 180

www.naftemporiki.gr638 × 399

https://el.wikipedia.org/wiki/Ανάλυση_Φουριέ

users.uoi.gr1199 × 816

https://www.physics4u.gr/articles/2003/decoherence.html

https://gate.iesl.forth.gr/~kafesaki/Modern-Physics/lectures/modern_physics5.html#c

https://el.wikipedia.org/wiki/Κβαντική_μηχανική

Αστροφυσική Πανεπιστημιακές εκδόσεις Kρήτης  Frank Shu

https://ebooks.edu.gr/modules/ebook/show.php/DSGL-C135/474/3139,12607/

a-kentavrou.blogspot.com1600 × 1200

www.g-physics.com506 × 140

ylikonet.gr320 × 135

Στο σημείο αυτό θέλω ακόμα να σημειώσω τις διαφορές στις ακτινοβολίες μεταξύ σύνθετου φωτός, μονοχρωματικού ασύμφωνου και μονοχρωματικού σύμφωνου φωτός γιατί ίσως δώσει κάτι χρήσιμο στην εξέλιξη

 Ενώ η επιρροή του σωματιδίου εξαπλώνεται στον χώρο