Σύντομη Βιοχημική Ιστορία των Οργανισμών Μέρος 2ο Οι μεγάλοι Νόμοι της Ενέργειας και το φαινόμενο της Ζωής Η Στατιστική Θερμοδυναμική. Στατιστική Κατανομή ταχυτήτων κατά Maxwell και ενέργειας κατά Maxwell- Boltzman

Σύντομη Βιοχημική Ιστορία των Οργανισμών Μέρος 2ο Οι μεγάλοι Νόμοι της Ενέργειας και το φαινόμενο της Ζωής Η Στατιστική Θερμοδυναμική. Στατιστική Κατανομή ταχυτήτων κατά Maxwell και ενέργειας κατά Maxwell- Boltzman

 Δήμητρα Σπανού, χημικός, μόνιμη καθηγήτρια στο 1ο Γυμνάσιο Δάφνης 

 

Η περιγραφή των διεργασιών της φύσης στις οποίες η Ενέργεια εμφανίζεται υπό μορφή θερμότητας

γίνεται μακροσκοπικά με την Θερμοδυναμική και μικροσκοπικά με την Στατιστική Μηχανική

Η ΘΕΡΜΟΔΥΝΑΜΙΚΗ ΚΑΙ Η ΣΤΑΤΙΣΤΙΚΗ ΜΗΧΑΝΙΚΗ 

Η Θερμοδυναμική που περιγράφει μακροσκοπικά τις ιδιότητες των φαινομένων της φύσης  στις οποίες η ενέργεια εμφανίζεται υπό μορφή θερμότητας.

Είναι φαινομενολογική δηλαδή βασίζεται στην επαληθεύσιμη παρατήρηση.

Η Κλασσική Θερμοδυναμική είναι βασίζεται στη έννοια των μακροσκοπικών συστημάτων. Ασχολείται μόνο με ανατρέψιμες διαδικασίες που γίνονται περνώντας μέσα από διαδοχικές καταστάσεις ισορροπίας που διαρκούν μεγάλο χρόνο και μπορεί να κατευθυνθούν με αντίθετη φορά, αλλάζοντας το πρόσημο των μετρήσεων.

Τα μακροσκοπικά συστήματα, όταν είναι σε ισορροπία, καθορίζονται από τις θερμοδυναμικές μεταβλητές που είναι η θερμοκρασία, η πίεση, ο όγκος και η Χημική Σύνθεση . Για να ολοκληρωθεί όμως η εικόνα και να κατανοηθούν τα μακροσκοπικά μεγέθη και να ερμηνευτούν οι μακροσκοπικοί νόμοι πρέπει να γίνει ερμηνεία βάσει μκροσκοπικών δεδομένων και αιτιών.

 Αυτό καταφέρνει η Στατιστική Θερμοδυναμική και Στατιστική Μηχανική που περιγράφουν τις διεργασίες της θερμοδυναμικής μικροσκοπικά και επικεντρώνεται στα μικρά δομικά σωματίδια της ύλης και τις ιδιότητές τους όπως η κινητικότητα και θέση. Περιγράφει μεγέθη της  φαινομενολογικής θερμοδυναμικής συνδέοντας με τις μέσες τιμές των μικροσωματιδίων, κι έτσι είναι  πιο σαφής από την θερμοδυναμική

ΣΤΑΤΙΣΤΙΚΗ ΘΕΡΜΟΔΥΝΑΜΙΚΗ ΚΑΙ ΣΤΑΤΙΣΤΙΚΗ ΜΗΧΑΝΙΚΗ

ΣΤΑΤΙΣΤΙΚΗ ΘΕΡΜΟΔΥΝΑΜΙΚΗ

Η Στατιστική Θερμοδυναμική συνδέει τις μακροσκοπικές θερμοδυναμικές ιδιότητες των συστημάτων (πίεση, θερμοκρασία, ειδική θερμότητα, εσωτερική ενέργεια κ.λ.π.) με τις μικροσκοπικές ιδιότητες των σωματιδίων (κυρίως μορίων) όπως , μέση ταχύτητα μορίων, μέση ελεύθερη διαδρομή μάζα σωματιδίων, μέση ορμή, και μέση κινητική ενέργεια μορίων, κυρίως θεωρητικά αλλά και με απλές μαθηματικές σχέσεις που καταλήγουν σε υπολογισμό μακροσκοπικών μεγεθών.

Βαθμοί ελευθερίας f σώματος στην Μηχανική είναι ο αριθμός των ανεξάρτητων κινήσεων που επιτρέπονται στο σώμα ή αν έχουμε πιο πολύπλοκη σύνδεση (μηχανισμός) τότε γίνεται ο αριθμός των πιθανών ανεξάρτητων σχετικών κινήσεων μεταξύ των τμημάτων του μηχανισμού. Παράδειγμα: Σχήμα πάνω σε επίπεδο έχει 3 βαθμούς ελευθερίας κίνησης και 2 για την θέση κάθε σημείου στο επίπεδο. Ένα μονοατομικό αέριο 3 βαθμούς (x, y,z.) Ενα διατομικό με ταλαντούμενη σύνδεση 7 (3 μεταφορική κίνηση, 2περιστροφική, 2ταλάντωση)  

Θεώρημα ισοκατανικής της ενέργειας: Συσχετίζει την θερμοκρασία που έχει ένα σύστημα λόγω της θερμότητας,- που προέρχεται από  του σύνολο των διαφόρων κινητικών ενεργειών του.

 Ισχυρίζεται πως η συνολική ενέργεια από κίνηση -μέση κινητική (μεταφορική, περιστροφική) και πιθανή ενέργεια (από ταλάντωση) του συστήματος από κίνηση μοιράζεται εξ ίσου μεταξύ των διαφόρων μορφών της.  Eμορίου =   f /2 kΒΤ

Το θεώρημα της ισοκατανομής κάνει και ποσοτικές προβλέψεις

Κάθε άτομο για κάθε βαθμό ελευθερίας  έχει μέση κινητική ενέργεια  1/2 kΒΤ     kΒ =σταθερά Boltzman, T θερμοκρασία στην κλίμακα Κέλβιν. Συνολικά  σε μονοατομικό αέριο κάθε έχει  κινητική ενέργεια  3/2 kΒΤ, σε διατομικό χωτίς ταλαντώσεις ατόμων δεσμού  έχει κινητική ενέργεια  5/2 kΒΤ ενώ διατομικό με ταλάντωση ατόμων δεσμού  5/2 kΒΤ   και με ταλάντωση ατόμων δεσμού  7/2 kΒΤ

Εάν πρόκειται για ποσότητα ενός mole η ποσότητα αυτή πολλαλπασιάζεται επί τον αριθμό των μορίων Ν και έχουμε για μονοατομικό

 Εmol= Ν f/2 kΒΤ =  f/2 RΤ   για n moles E=  f/2n RΤ

Εάν θεωρήσουμε κι άλλες μορφές ενέργειας του αερίου οι οποίες μπορεί να  αποδωθούν με το f  (γενικευμένα) τότε η εσωτερική ενέργεια παίρνει την μορφή U=  f/2 nRΤ  και από αυτό μπορούμε να υπολογίσουμε την μεταβολή της σε σ υνάρτηση με την μεταβολή της θερμοκρασίας ΔU=  f/2 nRΔΤ 

Σε ισόχωρες μεταβολές όπου το έργο είναι μηδέν έχουμε:    Q = ΔU=  f/2 nRΔΤ  αν  cv =f/2 R    τότε Q = ΔU= ncvΔΤ

Σε ισοβαρείς μεταβολές έχουμε  Q = ΔU + W  ή  Q =  ncvΔΤ + W

ΚΙΝΗΤΙΚΗ ΘΕΩΡΙΑ ΤΩΝ ΑΕΡΙΩΝ

Είναι ένας κλάδος της Στατιστικής Μηχανικής που εξηγεί τους νόμους των αερίων με βάση τα μικροσωματίδια που περιέχουν (ατομα, μόρια σε θερμοδυναμική ισορροπία) τα οποία βρίσκονται διαρκώς σε κίνηση.

 περιγάφει την κίνηση Ν σωματιδίων καθορίζοντας χωρικές συντεταγμένες και συντεταγμένες ταχύτητας σε 6διάστατο χώρο.

Οργανώνει, ομαδοποιεί  και αξιολογεί πληροφορίες ανά τομείς και δεδομένου πως δεν είναι δυνατό να περιγραφούν ξεχωριστά πληροφορίες για κάθε ένα σωματίδιο βγάζει μακροσκοπικά αποτελέσματα αξιοποιώντας τις τιμές των μέσων ταχυτήτων και των πιθανοτήτων

 Εξηγεί με βάση τις ιδιότητες των σωματιδίων εξηγεί τις μακροσκοπικές ιδιότητες των αερίων όπως Θερμοκρασία, Πίεση, Χημικά Συστατικά.

Με βάση αυτήν, η μέση κινητική ενέργεια ενός μεμονωμένου σωματιδίου με μάζα m και η μέση ταχύτητα δίνεται από σχέσεις:

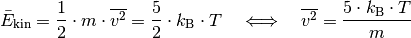
\bar{E}_{\mathrm{kin}} = \frac{1}{2} \cdot m \cdot \overline{v^2} = \frac{5}{2}\cdot k_{\mathrm{B}} \cdot T \quad \Longleftrightarrow \quad \overline{v^2} =\frac{5 \cdot k_{\mathrm{B}} \cdot T}{m}

Από αυτό φαίνεται ότι η μάζα ενός σωματιδίου  η μέση τετραγωνική ταχύτητα είναι μεγέθη αντίστροφα

Θεμελιώδης εξίσωση της κινητικής θεωρίας

Η Πίεση ενός αερίου και κατ'  επέκταση ενός ρευστού είναι αποτέλεσμα των ελαστικών κρούσεων των σωματιδίων του και της μεταφοράς κινητικής ενέργειας. Ισχύει η σχέση: 

     p &= \frac{m}{V} \cdot N \cdot \overline{v_{\mathrm{x}}^2} \\[4pt]\Rightarrow p \cdot V &= N \cdot m \cdot \overline{v_{\mathrm{x}}^2} \\[4pt]

εξαρτάται από την ποσότητα της ουσίας σε  γραμμάρια (n= αριθμός moles και M= μοριακό βάρος) ή σε αριθμό μορίων Ν ,  m ( μάζα του μορίου), V( όγκος που καταλαμβάνει η ουσία), την μέση τετραγωνική ταχύτητα των σωματιδίων (μορίων) 

H ερμηνεία αυτής της εξίσωσης οδηγεί σε συνδέσεις μεταξύ μεταβλητών μεγεθών ενός θερμοδυναμικού συστήματος και  του μεγέθους των σωματιδίων του

  • αν Nm ή  nM μας δίνει την συνολική μάζα της ουσίας  και V είναι ο όγκος στον οποίο βρίσκεται τότε nM/V  = Nm/V =ρ (πυκνότητα σε gr/ml ή gr/lt  ή kgr/m3 κ.λ.π.  Τότε ο παραπάνω τύπος (που αποτελεί  την θεμελιώδης εξίσωση στατιστικής θερμοδυναμικής) δίνει μια σχέση με την πυκνότητα  

Ekin = 3/2kT     k σταθερά του boltzman

ΣΤΑΤΙΣΤΙΚΗ ΚΑΤΑΝΟΜΗ ΤΑΧΥΤΉΤΩΝ ΚΑΙ ΕΝΕΡΓΕΙΩΝ ΜΟΡΙΩΝ

 ΚΑΙ ΟΙ ΕΞΙΣΩΣΕΙΣ MAXWELL ΚΑΙ MAXWELL -BOLTZMAN

Μέχρι εδώ η αναφορά στην ταχύτητα και ενέργεια των μορίων του αερίου, έγινε με την χρήση της μέσης ταχύτητας.

Σε πολλά προβλήματα όμως ενδιαφέρει και η κατανομή των ταχυτήτων και των ενεργειών σε διάφορες τιμές αλλά και η πιθανότερη κατανομή στην οποία το σύστημα βρίσκεται σε κατάσταση ισορροπίας.

 

Η μέση ταχύτητα των σωματιδίων (άτομα ή μόρια αερίου σε σύστημα που βρίσκεται σε θερμοδυναμική ισορροπία)

 τη σχέση: υ=(w1+w2+...wi)/N

όπου w είναι η ταχύτητα των σωματιδίων και Ν ο αριθμός τους

Επίσης η πιθανότερη ταχύτητα α  δίνεται από την κατανομή Boltzman . 

Η σχέση της α, της μέση ταχύτητας υ και της μέσης  τετραγωνικής ταχύτητας u είναι 

α:υ:u =1:1,28:1,224

 

 

ΚΑΤΑΝΟΜΗ ΤΑΧΥΤΗΤΩΝ ΑΕΡΙΩΝ ΚΑΤΑ MAXWELL

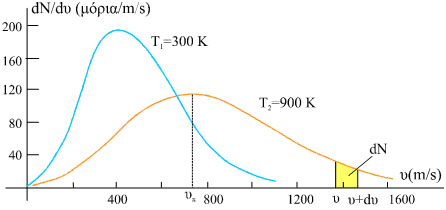
Στην ισορροπία μεταξύ των μορίων των αερίων με P, V σταθερά, συμβαίνουν διαρκώς ελαστικές κρούσεις και οι ταχύτητες των μορίων wi μεταβάλλονται διαρκώς ενώ η συνολική ενέργεια παραμένει σταθερή. Η στατιστική που δίνει την κατανομή των έγινε από τον Maxwell

PHYSIC LESSONS: ΚΑΤΑΝΟΜΗ ΚΑΤΑ MAXWELL-BOLTZMANN (ΜΑΞΓΟΥΕΛ - ΜΠΟΛΤΣΜΑΝ)

 

O Maxwell μελέτησε τις διαφορετικές ταχύτητες των μορίων και την κατανομή τους από 0 έως άπειρο και υπολόγισε τα ποσοτά τους σε διάφορες περιοχές τιμών. Η πυκνότητα πιθανότητας για dn σωματίδια να βρίσκονται σε περιοχή ταχυτήτων u , u+du  ως dn =f(u)du για συγκεκριμένη θερμοκρασία δίνεται από την συνάρτηση πιθανότητας:

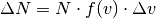
\Delta N = N \cdot f(v) \cdot \Delta v

 

 

Στην κατανομή των μορίων του αζώτου σε περιοχές ταχυτήτων επαληθεύεται η στατιστική κατανομή  κατά Boltzman 

 

ΣΤΑΤΙΣΤΙΚΗ ΚΑΤΑΝΟΜΗ ΚΑΤΑ MAXWELL-BOLTZMΑΝ ΤΩΝ ΕΝΕΡΓΕΙΩΝ ΤΩΝ ΜΟΡΙΩΝ 

Αν θεωρήσουμε Ν1 σωματίδια στην κατάσταση 1 , Ν2 στην κατάσταση 2 ...Νι στην κατάσταση ι  τότε το σύνολο τους είναι: ΣΝι =Ν1 +Ν2 +Ν3+   Νι 

Η συνολική τους ενέργεια είναι άθροισμα  από τις  ενέργειες που έχουν σε αντίστοιχες καταστάσεις ι και  είναι  ΣΝιΕι =  Ν1Ε1  + Ν2Ε2  +...ΝιΕι

Οι ενέργειες των σωματιδίων (άτομα, μόρια, σε θερμοδυναμική ισορροπία))  ακολουθούν την κατανομή Maxwell Boltzman 

 

ΣΤΑΤΙΣΤΙΚΗ ΜΗΧΑΝΙΚΗ

Σε ένα ανώτερο επίπεδο, η Θερμοδυναμική, χρησιμοποιεί την Στατιστική Μηχανική η οποία περιλαμβάνει την κινητική θεωρία των αερίων

 Η ¨Κινητική θεωρία των Αερίων"  επεκτείνεται στην "Κινητική Θεωρία των ρευστών" και σύμφωνα με την θεωρία αυτήν, τα σωματίδια από τα οποία  αποτελούνται τα ρευστά βρίσκονται σε διαρκή άτακτη κίνηση 

Η θερμοκρασία αποτελεί εκδήλωση της κίνησης αυτής. 

Επίσης,  οδηγούνται σε ελαστικές κρούσεις μεταξύ τους και με τα τοιχώματα του δοχείου που περιέχονται δημιουργώντας συνολικά την πίεση των αερίων

Για τον υπολογισμό των μακροσκοπικών μεγεθών Πίεση και Θερμοκρασία εισάγονται τα μεγέθη μέση τετραγωνική ταχύτητα u, μάζα μορίου m αριθμός μορίων Ν. Βάσει υπολογισμών υπολογίζονται από αυτά, μακροσκοπικά μεγέθη όπως η Πίεση και η Θερμοκρασία. 

 

PV = 2/3 NEkin =1/3nNmu2    (Ekin=1/2mu2)

PV= 2/3 .3/2NkT =NkT    ->  T=PV/Νk

-> PV = NkT = 1/3nNmu2   ->T= 1/3nNmu2 /R

Από την Στατιστική Μηχανική παίρνουμε θεμελιώδεις θερμοδυναμικές εξισώσεις

Ο ορισμός για την πίεση  και η σχέση της στατιστικής μηχανικής στην θερμοδυναμική παίρνει τις παρακάτω μορφές, ανάλογα με το περίο αναφοράς.

  Πίεση στην στατιστική μηχανική σε μικροκανονικό σύνολο  δίνεται από την μερική παράγωγο  εσωτερική ενέργεια  των μορίων U= U(S, V, n) η οποία αποτελεί και την αρχική μορφή της καταστατικής εξίσωσης των αερίων και την θεμελι'ωδη εξίσωση της θερμοδυναμικής.( S εντροπία, V όγκος, n ποσότητα ουσίας. 

παραγωγίζοντας παίρνουμε dU =(θU/θS)Vn .dS  + (θU/θV)Sn .dV  +Σ (θU/θni)SV .dni . =TdS - pdV +μdn  Από τους ορισμούς της θερμοκρασίας Τ, της πίεσης ρ και του χημικού δυναμικού μ.  Για κλειστό σύστημα  dU = TdS - pdV 

  Πίεση στην στατιστική μηχανική σε μεγαλοκανονικό σύνολο δίνεται από την μερική παράγωγο  της ελεύθερης F ενέργειας που μπορεί να δώσει έργο. 

  Πίεση στην στατιστική μηχανική σε μεγάλης κλίμακας κανονικό σύνολο δίνεται από την  Ενέργεια  Lundow σε συστήματα που ανταλλάσουν ενέργεια και έργο με το περιβάλλον .  

Δήμητρα Σπανού

 

ΠΗΓΕΣ

https://www.spektrum.de/lexikon/physik/thermodynamik-und-statistische-mechanik/14461

https://ebooks.edu.gr/ebooks/v/html/8547/2684/Fysiki_B-Lykeiou-ThSp_html-empl/index4_9.html

https://www.chemie.de/lexikon/Irreversibilit%C3%A4t.html

Πίεση (φυσική) - Βικιπαίδεια (wikipedia.org)

https://eclass.uowm.gr/modules/document/file.php/MECH261/15_%CE%9A%CE%95%CE%A6.pdf

https://www.hellenicaworld.com/Science/Physics/gr/TheorimaIsokatanomis