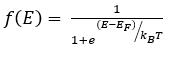Δήμητρα Σπανού, χημικός, καθηγήτρια Β/θμιας Εκπ/σης στο 1ο Γυμν. Δάφνης
ΚΛΑΣΣΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΚΑΙ ΚΒΑΝΤΙΚΗ ΣΤΑΤΙΣΤΙΚΗ
Στην κλασσική στατιστική όλα τα σωματίδια, θεμελιώδη και σύνθετα, (ηλεκτρόνια, άτομα, μόρια..)
α.είναι διακριτά που σημαίνει πως κανένα από τα σωματίδια αυτά δεν μπορεί να καταλάβει την ίδια ενεργειακή κατάσταση με άλλο χωρίς αυτό έχει επίδραση στις ιδιότητες του συστήματος.
β. Μπορούν να τοποθετηθούν σε οποιανδήποτε κατάσταση προσβάσιμη από το σύστημα
Ένα μέρος της Στατιστικής Μηχανικής χρησιμοποιεί επίσης αρχές της Κβαντικής Μηχανικής (Κβαντική Στατιστική).
Στην κβαντική στατιστική τα σωματίδια ορισμένου τύπου
α. δεν διακρίνονται μεταξύ τους και
β. η ανταλλαγή οποιουδήποτε σωματιδίου δεν αλλάζει την κατάσταση του συστήματος
Αυτό σημαίνει ότι η κυματική συνάρτηση του συστήματος παραμένει αμετάβλητη σε σχέση με την ανταλλαγή σωματιδίων
Αν το σύστημα αποτελείται από διαφορετικά σωματίδια (όπως πρωτόνια και ηλεκτρόνια) η κυματική συνάρτηση παραμένει ίδια μέχρι μια φάση ξεχωριστά για το κάθε είδος σωματιδίων
Τα σωματίδια μπορεί να εκληφτούν σαν κβαντικά εάν είναι γνωστοί οι βαθμοί ελευθερίας τους που σχετίζονται με το εξεταζόμενο θέμα. Όλα τα κβαντικά έχουν τρεις βαθμούς ελευθερίας μεταφορικής κίνησης και έναν από spin
ΣΤΟΙΧΕΙΩΔΗ ΣΩΜΑΤΙΔΙΑ ΚΑΙ ΣΥΝΘΕΤΑ ΣΩΜΑΤΙΔΙΑ
Στοιχειώδη σωματίδια είναι τα μικρότερα σωματίδια της ύλης που έχουν ανακαλυφθει έως σήμερα και για τον λόγο αυτό δεν αποτελούνται από άλλα μικρότερα αλλά αποτελούν δομικά στοιχεία άλλων υποατομικών σωματων σύνθετων όπως το νετρόνιο, πρωτόνιο, μεσόνιο
τα στοιχειώδη σωματίδια διακρίνονται
σωματίδια δομής που είναι φερμιόνια περιλαμβάνουν τα κουαρκς και τα λεπτόνια και συμμετέχουν στη δομή της ύλης
και σε σωματίδια φορείς που είναι μποζόνια, περιλαμβάνουν τα φωτόνια (ηλεκτρομαγνητική δύναμη) τα W και Z μποζόνια (ασθενής αλληλεπίδραση), το γλουόνιο (ισχυρή αλληλεπίδραση) και το υποθετικό βαρυτόνιο (βαρυτική αλληλεπίδραση) και είναι φορείς δυνάμεων
Τα Σύνθετα σωματίδια είναι συνδυασμοί κουαρκς και αντικουαρκς είναι τα
Αδρόνια που είναι και περιλαμβάνουν τα μποζόνια μεσόνια (πιόνια, καόνια ...) που είναι άρτιοικαι τα φερμιόνια βαριόνια (πρωτόνιο (3 κουαρκς), νετρόνιο (3 κουαρκς)κ.α. ...) που αποτελούνται από περιττό αριθμό κουαρκς
Αδρόνια με αριθμό κουαρκς ή κουαρκς και αντικουαρκς μεγαλύτερο του τρια βρέθηκαν και ονομάστηκαν Εξωτικά αδρόνια όπως το
ΦΕΡΜΙΟΝΙΑ ΚΑΙ ΜΠΟΖΟΝΙΑ
Τα σύνθετα φερμιόνια και τα σύνθετα μποζόνια ονομάζονται από κοινού αδρόνια
Φερμιόνια: Είναι σωματίδια που υπακούουν στις αρχές του Pauli και έχουν διαφορετική την τετράδα των κβαντικών αριθμών τους (3 για την κίνηση και ένας για το spin). Ένα σύστημα μπορεί να αποτελείται από πολλά μή αλληλοεπιδρώντα διαφορετικά πανομοιότυπα τέτοια σωματίδια
Έχουν την χαρακτηριστική ιδιότητα να σχηματίζουν πλήρως αντισυμμετρικές σύνθετες κβαντικές καταστάσεις. Αυτό έχει σαν αποτέλεσμα από τα στοιχειώδη σωματίδια να δημιουργούνται συνθετότερα σώματα/τίδια όπως π.χ. το άτομο που αποτελείται από πρωτόνια, νετρόνια και ηλεκτρόνια και εν τέλει είναι τα σωματίδια που φτιάχνουν την ύλη
Όπως αναφέρθηκε τα απλά κβαντικά σωματίδια έχουν 4 βαθμούς ελευθερίας 3 για την μεταφορική κίνηση και 1 για το spin ημιακέραιος αριθμός (1/2, 3/2,... )
Τα φερμιόνια περιλαμβάνουν:
τα βαρυόνια δηλαδή τα πρωτόνια, τα νετρόνια, τα αντιπρωτόνιο, τα βαρυόνια (από 3 κουαρκς) τα πεντακουαρκς (4 κουαρκ κι ένα αντικουαρκ), τα υπερόνια
τα κουαρκς δηλαδή τα t κουαρκ
τα λεπτόνια δηλαδή τα ηλεκτρόνια, τα λεπτόνια, τα αντινετρίνα, τα μιόνια, τα ποζιτρόνια, τα νετρίνα, κ.α.
To μεγαλύτερο ποσοστό της μάζας της συνηθισμένης ύλης προέρχεται από δύο αδρόνια το πρωτόνιο και το νετρόνιο που ανήκουν στα βαρυόνια
Μποζόνια είναι τα σωματίδια που μεταφέρουν ενέργεια και επομένως είναι σωματίδια αλληλεπίδρασης. Παραδείγματα το φωτόνιο (ηλεκτρομαγνητικά κύματα), το φωνόνιο (ελαστικές παραμορφώσεις) Τα μποζόνια έχουν ακέραιο αριθμό spin (0, 1, 2...).
Τρεις θεμελιώδεις αλληλεπιδράσεις, η ηλεκτρομαγνητική, η ισχυρή και ασθενής πυρηνική έχουν μποζόνια με spin 1(φωτόνια, γλουόνια και Ζ,W+-)
Στη φύση υπάρχουν στοιχειώδη σωματίδια αλλά και σύνθετα όπως τα μεσόνια αλλά και ακόμα συνθετότερα όπως το άτομα του Ηλίου-4 (spin =0), με 2 πρωτόνια και δύο νετρόνια στον πυρήνα και δύο ηλεκτρόνια σε στοιβάδα αλλά και το τανυστικό μποζόνιο βαρυτόνιο με spin =2.
Κατά κανόνα τα άτομα που έχουν το σύνολο των πρωτονίων και νετρονίων και ηλεκτρονίων άρτιο αριθμό, είναι μποζόνια
Ακόμα το βαθμωτό σωματίδιο Higgs (spin=0) που αποτελεί σωματίδιο του πεδίου δίνει μάζα στα σωματίδια
Όλα αυτά είναι μποζόνια με ακέραιο spin. Τα μποζόνια δεν περιορίζονται από την απαγορευτική αρχή του Pauli και μπορούν να βρίσκονται στην ίδια κατάσταση στην ίδια περιοχή του χώρου
Θεώρημα spin στατιστικης Τα σωματίδια με ημιακέραιο spin (1/2, 3/2, 5/2,...) μπορούν να βρίσκονται το πολύ ένα σε κάθε μια κατάσταση
Τα σωματίδια με ακέραιο spin (1,2,3...) μπορούν να είναι οσαδήποτε σε κάθε κατάσταση
ΚΑΤΑΝΟΜΕΣ ΦΕΡΜΙΟΝΙΩΝ ΚΑΙ ΜΠΟΖΟΝΙΩΝ ΣΕ ΣΤΑΘΜΕΣ ΕΝΕΡΓΕΙΑΣ
ΚΑΤΑΝΟΜΗ FERMI- DIRAC
Τα φερμιόνια απαγορεύεται από την αρχή αποκλεισμού του Pauli να μπορούν να βρίσκονται σε κάθε μια κβαντική κατάσταση περισσότερα από ένα
Είναι η πιθανότητα κατάληψης μιας στάθμης ενέργειας από φερμιόνια είναι εφαρμογή κβαντικής στατιστικής, και δίνεται με τη εξίσωση Fermi - Dirac
Όπως ξέρουμε τα φερμιόνια αποτελούν δυσδιάκριτα πανομοιότυπα σωματίδια, που υπακούουν στις αρχές του Pauli και το spin τους είναι ημιακέραιος (1/2, 3/2, 5/2, ...) είναι δηλαδή φερμιόνια.
Τα σωματίδια αυτά πρέπει επίσης να είναι μονοσωματίδια ή σύνθετα σωματίδια που δεν επιδρούν μεταξύ τους
Η πιθανότητα η διαθέσιμη κατάσταση Ε να καταλαμβάνεται από ένα ηλεκτρόνιο σε κατάσταση ισορροπίας, δίνεται από τη συνάρτηση
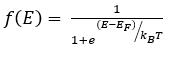

Fermi- Dirac όπου k η σταθερά Boltzman,
Τ η απόλυτη θερμοκρασία,
ΕF τo επίπεδο ενέργειας Fermi E η ενεργειακή κατάσταση ενός σωματιδίου ι και
μ το συνολικό χημικό δυναμικο

Υπάρχει μια οριακή περίπτωση μεγάλης ενέργειας όπου το σύστημα περνά στην στατιστική Boltzman
Η ενεργειακή κατανομή Fermi- Dirac εφαρμόζεται και για ηλεκτρόνια τα οποία έχουν spin 1/2
Η κατανομή Fermi- Dirac ισχύει μόνο εάν ο αριθμός των φερμιονίων είναι αρκετά μεγάλος ώστε η προσθήκη ενός ακόμα να μην επιρρεάζει.
Η κατανομή Fermi- Dirac χρησιμοποιήθηκε το από τον Ralph Fawel το 1926 για να περιγράψει την κατάρευση ενός αστεριού σε λευκό νάνο
ΚΑΤΑΝΟΜΗ BΟSE EINSTEIN
Η κατανομή Bose Einstein είναι μια κατανομή πιθανοτήτων στην κβαντική Στατιστική συστήματος πολλών δυσδιάκριτων σωματιδίων με 4 μεταβλητές (x, y, z για την τοποθεσία και m για το spin), για τα οποία η κυματική συνάρτηση Ψ δεν αλλάζει πρόσημο όταν ανταλλάσσονται οι μεταβλητές, αντίθετα με την αντίστοιχη στατιστική για τα φερμιόνια. Πολλά μποζόνια μπορεί να βρίσκονται στην ίδια κατάσταση ενός σωματιδίου, δηλαδή, να έχουν τους ίδιους κβαντικούς αριθμούς.
Εφόσον δεν υπάρχει αλληλεπίδραση ο αριθμός των μποζονίων n σε συνάρτηση της ενέργειας Ε δίνεται από τη σχέση
όπου μ το χημικό δυναμικό με την χαμηλότερη δυνατή τιμή ενέργειας, β η ενεργειακή τυποποίηση που εξαρτάται από την κλίμακα της θερμοκρασίας που χρησιμοποιούμε.
n(Ε) δίνει των αριθμό των γλουονίων που κατέχει μια κβαντική κατάσταση.
Υπάρχουν όμως και
Κάτω από μια πολύ χαμηλή θερμοκρασία όπου υπάρχει πλέον ελευθερία αλληλεπίδρασης
ΣΥΜΠΥΚΝΩΜΑΤΑ ΦΕΡΜΙΟΝΙΩΝ (FERMI- DIRAC) ΚΑΙ ΜΠΟΖΟΝΙΩΝ (BOSE EINSTEIN)
Η ΠΕΜΠΤΗ ΚΑΙ ΕΚΤΗ ΜΟΡΦΗ ΤΗΣ ΥΛΗΣ
ΣΥΜΠΥΚΝΩΣΗ ΜΠΟΖΟΝΙΩΝ
Μποζόνια, δηλαδή δυσδιάκριτα σωματίδια η πλειοψηφία των οποίων βρίσκονται στην ίδια κβαντομηχανική κατάσταση, σε ακραίες συνθήκες υφίστανται συσσωμάτωση και δημιουργούν ένα συμπύκνωμα που λέγεται συμπύκνωμα Bose - Einstein
Το 1995 οι επιστήμονες κατάφεραν να σχηματίσουν την πέμπτη μορφή της γνωστής έως τότε ύλης (στρεά, υγρή , αέρια, πλάσμα. Αυτό ήταν ένα στην ίδια κβαντομηχανική κατάσταση υπερσωματίδιο που σχηματίστηκε από την συγχώνευση ψυχρών μποζονίων. Έμοιαζε περισσότερο σαν κύμα παρά σαν ένα κομμάτι ύλης. Εάν συμπέσουν οι κβαντικοί αριθμοι (επιτρεπτό για τα μποζόνια) πολλά μποζόνια μπορεί να βρεθούν στην ίδια κατάσταση
Η συμπύκνωση Bose Einstein είναι μια κατάσταση συσσωμάτωσης δυσδιάκριτων σωματιδίων (μποζονίων ) που βρίσκονται σε πολύ χαμηλή θερμοκρασία , κάτω από 1μΚ. Σε τόσο χαμηλές θερμοκρασίες, το μήκος κύματος των σωματιδίων- κυμάτων κατα de broglie, λ=h/mu λόγω της χαμηλής θερμοκρασίας γίνεται μικρό τόσο που υπερβαίνει τα μεσοατομικά διαστήματα και έτσι όλα τα άτομα έχουν εννιαία κυματοσυνάρτηση.
Τα μποζόνια που έχουν σπιν, ακέραιο πολλαπλάσιο, (0, h/2π, 2h/2π, 3h/2π...) έχουν καταρρεύσει στην ίδια κβαντική κατάσταση και δημιουργείται το συσσωμάτωμα που έχει και την έννοια κύματος.
Για πρώτη φορά συμπύκνωμα Bose Einstein παρατηρήθηκε σε ατμούς ρουβίδιου και δημιουργήθηκε συσσωμάτωμα 2000ατόμων 10μm που επέζησε 15min.
Με ανάλογοα πειράματα έχουν δημιουργηθεί και άλλα συσσωματώματα Bose Einstein όπως χαλκού και λιθίου
ΠΗΓΕΣ
https://en.wikipedia.org/wiki/Fermi%E2%80%93Dirac_statistics
https://de.wikipedia.org/wiki/Bose-Einstein-Kondensat
https://el.jf-parede.pt/what-is-fermi-dirac-distribution
https://en.wikipedia.org/wiki/Particle_statistics
https://www.firstscience.com/SITE/ARTICLES/new.asp
https://www.studocu.com/gr/document/eoniko-metsobio-polytexneio/maths-3/fermions-and-bosons/43431326
https://de.wikipedia.org/wiki/Bose-Einstein-Statistik
https://el.wikipedia.org/wiki/%CE%9A%CE%BF%CF%85%CE%AC%CF%81%CE%BA
https://el.wikipedia.org/wiki/%CE%9C%CF%80%CE%BF%CE%B6%CF%8C%CE%BD%CE%B9%CE%BF
https://www.firstscience.com/SITE/ARTICLES/new.asphttps://www.researchgate.net/figure/Degenerate-bosons-fermions-and-SUN-fermions-Unlike-bosons-which-can-occupy-the-same_fig1_344002230
https://en.wikipedia.org/wiki/Hadron
https://www.semanticscholar.org/paper/Interacting-bosons-and-fermions-in-optical-lattice-Will/e081b3dad5eb6cb849aa9eb38dc358d09ec198c4
https://physics4u.gr/blog/2018/02/22/%CE%BC%CF%80%CE%BF%CE%B6%CF%8C%CE%BD%CE%B9%CE%BF-%CE%BA%CE%B1%CE%B9-%CF%80%CE%B5%CE%B4%CE%AF%CE%BF-higgs/
https://www.physics4u.gr/articles/bec.html
Η στατιστική Fermi–Dirac εφαρμόζεται πιο συχνά σε ηλεκτρόνια, έναν τύπο φερμιονίου με σπιν 1/2.
Ένα αντίστοιχο της στατιστικής Fermi–Dirac είναι η στατιστική Bose–Einstein, η οποία ισχύει για πανομοιότυπα και δυσδιάκριτα σωματίδια με ακέραιο σπιν (0, 1, 2, κ.λπ.) που ονομάζονται μποζόνια. Στην κλασική φυσική, η στατιστική Maxwell–Boltzmann χρησιμοποιείται για να περιγράψει σωματίδια που είναι πανομοιότυπα και αντιμετωπίζονται ως διακριτά. Και για τις στατιστικές Bose–Einstein και Maxwell–Boltzmann, περισσότερα από ένα σωματίδια μπορούν να καταλαμβάνουν την ίδια κατάσταση, σε αντίθεση με τις στατιστικές Fermi–Dirac. Σύγκριση της μέσης πληρότητας της βασικής κατάστασης για τρεις στατιστικές Ιστορία Πριν από την εισαγωγή της στατιστικής Fermi–Dirac το 1926, η κατανόηση ορισμένων πτυχών της συμπεριφοράς των ηλεκτρονίων ήταν δύσκολη λόγω φαινομενικά αντιφατικών φαινομένων. Για παράδειγμα, η ηλεκτρονική θερμική ικανότητα ενός μετάλλου σε θερμοκρασία δωματίου φαινόταν να προέρχεται από 100 φορές λιγότερα ηλεκτρόνια από ό,τι στο ηλεκτρικό ρεύμα.[3] Ήταν επίσης δύσκολο να καταλάβουμε γιατί τα ρεύματα εκπομπής που παράγονται από την εφαρμογή υψηλών ηλεκτρικών πεδίων σε μέταλλα σε θερμοκρασία δωματίου ήταν σχεδόν ανεξάρτητα από τη θερμοκρασία. Η δυσκολία που συναντούσε το μοντέλο Drude, η ηλεκτρονική θεωρία των μετάλλων εκείνη την εποχή, οφειλόταν στο ότι τα ηλεκτρόνια ήταν (σύμφωνα με την κλασική θεωρία της στατιστικής) όλα ισοδύναμα. Με άλλα λόγια, πιστευόταν ότι κάθε ηλεκτρόνιο συνεισέφερε στην ειδική θερμότητα μια ποσότητα της τάξης της σταθεράς Boltzmann kB. Αυτό το πρόβλημα παρέμεινε άλυτο μέχρι την ανάπτυξη της στατιστικής Fermi–Dirac. Οι στατιστικές Fermi–Dirac δημοσιεύθηκαν για πρώτη φορά το 1926 από τον Enrico Fermi[1] και τον Paul Dirac.[2] Σύμφωνα με τον Μαξ Μπορν, ο Πασκουάλ Τζόρνταν ανέπτυξε το 1925 τις ίδιες στατιστικές, τις οποίες ονόμασε στατιστικές Pauli, αλλά δεν δημοσιεύθηκαν εγκαίρως.[4][5][6] Σύμφωνα με τον Dirac, μελετήθηκε για πρώτη φορά από τον Fermi, και ο Dirac το ονόμασε "Fermi statistics" και τα αντίστοιχα σωματίδια "fermions".[7] Η στατιστική Fermi–Dirac εφαρμόστηκε το 1926 από τον Ralph Fowler για να περιγράψει την κατάρρευση ενός αστεριού σε έναν λευκό νάνο.[8] Το 1927 ο Arnold Sommerfeld το εφάρμοσε στα ηλεκτρόνια των μετάλλων και αναπτύχθηκε
Για ένα σύστημα πανομοιότυπων φερμιονίων σε θερμοδυναμική ισορροπία, ο μέσος αριθμός φερμιονίων σε κατάσταση μονοσωματιδίου i δίνεται από την κατανομή Fermi–Dirac (F–D),
Η κατανομή Fermi–Dirac είναι έγκυρη μόνο εάν ο αριθμός των φερμιονίων στο σύστημα είναι αρκετά μεγάλος, ώστε η προσθήκη ενός ακόμη φερμιονίου στο σύστημα να έχει αμελητέα επίδραση στο μ.[15] Δεδομένου ότι η κατανομή Fermi-Dirac προήλθε χρησιμοποιώντας την αρχή αποκλεισμού Pauli, η οποία επιτρέπει το πολύ σε ένα φερμιόνιο να καταλάβει κάθε δυνατή κατάσταση, το αποτέλεσμα είναι ότι
Σε μηδενική απόλυτη θερμοκρασία, το μ είναι ίσο με την ενέργεια Fermi συν τη δυναμική ενέργεια ανά φερμιόνιο, υπό την προϋπόθεση ότι βρίσκεται σε γειτονιά θετικής φασματικής πυκνότητας. Στην περίπτωση ενός φασματικού κενού, όπως για τα ηλεκτρόνια σε έναν ημιαγωγό, το μ, το σημείο συμμετρίας, ονομάζεται τυπικά επίπεδο Fermi ή —για τα ηλεκτρόνια— ηλεκτροχημικό δυναμικό, και θα βρίσκεται στο μέσο του διακένου. 13][14] Η διακύμανση του αριθμού των σωματιδίων στην κατάσταση i μπορεί να υπολογιστεί από την παραπάνω έκφραση για � {\displaystyle V(n_{i})=k_{\rm {B}}T{\frac {\partial }{\partial \mu }}{\bar {n}}_{i}={\bar { n}}_{i}(1-{\bar {n}}_{i}).} Κατανομή σωματιδίων πάνω από την ενέργεια Συνάρτηση Fermi � {\displaystyle F(\varepsilon )} με μ = 0,55 eV για διάφορες θερμοκρασίες στην περιοχή 50 K ≤ T ≤ 375 K Από την κατανομή Fermi–Dirac των σωματιδίων σε καταστάσεις, μπορεί κανείς να βρει την κατανομή των σωματιδίων πάνω από την ενέργεια.[nb 3] Ο μέσος αριθμός φερμιονίων με ενέργεια � Το \varepsilon _{i} μπορεί να βρεθεί πολλαπλασιάζοντας την κατανομή Fermi–Dirac � g_{i} (δηλαδή ο αριθμός των καταστάσεων με ενέργεια �
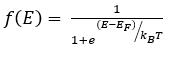
Ένα φερμιονικό συμπύκνωμα (ή συμπύκνωμα Fermi-Dirac) είναι μια υπερρευστή φάση που σχηματίζεται από φερμιονικά σωματίδια σε χαμηλές θερμοκρασίες. Σχετίζεται στενά με το συμπύκνωμα Bose-Einstein, μια υπερρευστή φάση που σχηματίζεται από άτομα μποζονίου υπό παρόμοιες συνθήκες. Το παλαιότερο αναγνωρισμένο φερμιονικό συμπύκνωμα περιέγραψε την κατάσταση των ηλεκτρονίων σε έναν υπεραγωγό. Η φυσική άλλων παραδειγμάτων, συμπεριλαμβανομένης της πρόσφατης εργασίας με φερμιονικά άτομα είναι ανάλογη. Το πρώτο ατομικό φερμιονικό συμπύκνωμα δημιουργήθηκε από μια ομάδα με επικεφαλής την Deborah S. Jin χρησιμοποιώντας άτομα καλίου-40 στο Πανεπιστήμιο του Κολοράντο Boulder το 2003.[1][2]
Ιστορικό
Υπερρευστότητα
Τα φερμιονικά συμπυκνώματα επιτυγχάνονται σε χαμηλότερες θερμοκρασίες από τα συμπυκνώματα Bose-Einstein. Τα φερμιονικά συμπυκνώματα είναι ένας τύπος υπερρευστού. Όπως υποδηλώνει το όνομα, ένα υπερρευστό έχει ιδιότητες ρευστού παρόμοιες με εκείνες που έχουν τα συνηθισμένα υγρά και αέρια, όπως η έλλειψη συγκεκριμένου σχήματος και η ικανότητα ροής ως απόκριση στις ασκούμενες δυνάμεις. Ωστόσο, τα υπερρευστά έχουν κάποιες ιδιότητες που δεν εμφανίζονται στη συνηθισμένη ύλη. Για παράδειγμα, μπορούν να ρέουν με υψηλές ταχύτητες χωρίς να διαχέουν ενέργεια - δηλ. μηδενικό ιξώδες. Σε χαμηλότερες ταχύτητες, η ενέργεια διαχέεται με το σχηματισμό κβαντισμένων στροβίλων, οι οποίες λειτουργούν ως «τρύπες» στο μέσο όπου διασπάται η υπερρευστότητα. Η υπερρευστότητα ανακαλύφθηκε αρχικά στο υγρό ήλιο-4 του οποίου τα άτομα είναι μποζόνια και όχι φερμιόνια.
Φερμιονικά υπερρευστά
Είναι πολύ πιο δύσκολο να παραχθεί ένα φερμιονικό υπερρευστό από ένα μποσονικό, επειδή η αρχή του αποκλεισμού Pauli απαγορεύει τα φερμιόνια να καταλαμβάνουν την ίδια κβαντική κατάσταση. Ωστόσο, υπάρχει ένας πολύ γνωστός μηχανισμός με τον οποίο μπορεί να σχηματιστεί ένα υπερρευστό από φερμιόνια: Αυτός ο μηχανισμός είναι η μετάβαση BCS, που ανακαλύφθηκε το 1957 από τον J. Bardeen, L.N. Cooper και R. Schrieffer για την περιγραφή της υπεραγωγιμότητας. Αυτοί οι συγγραφείς έδειξαν ότι, κάτω από μια συγκεκριμένη θερμοκρασία, τα ηλεκτρόνια (τα οποία είναι φερμιόνια) μπορούν να ζευγαρώσουν για να σχηματίσουν δεσμευμένα ζεύγη γνωστά τώρα ως ζεύγη Cooper. Όσο οι συγκρούσεις με το ιοντικό πλέγμα του στερεού δεν παρέχουν αρκετή ενέργεια για να σπάσουν τα ζεύγη Cooper, το υγρό ηλεκτρονίων θα μπορεί να ρέει χωρίς διασκορπισμό. Ως αποτέλεσμα, γίνεται υπερρευστό και το υλικό μέσω του οποίου ρέει υπεραγωγός.
Η θεωρία BCS ήταν εκπληκτικά επιτυχημένη στην περιγραφή υπεραγωγών. Λίγο μετά τη δημοσίευση της εργασίας BCS, αρκετοί θεωρητικοί πρότειναν ότι ένα παρόμοιο φαινόμενο θα μπορούσε να συμβεί σε ρευστά που αποτελούνται από φερμιόνια διαφορετικά από ηλεκτρόνια, όπως τα άτομα ηλίου-3. Αυτές οι εικασίες επιβεβαιώθηκαν το 1971, όταν πειράματα που πραγματοποιήθηκαν από τον D.D. Ο Osheroff έδειξε ότι το ήλιο-3 γίνεται υπερρευστό κάτω από 0,0025 K. Σύντομα επαληθεύτηκε ότι η υπερρευστότητα του ηλίου-3 προκύπτει από έναν μηχανισμό παρόμοιο με το BCS.[a]



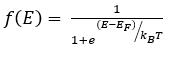
 Fermi- Dirac όπου k η σταθερά Boltzman, Τ η απόλυτη θερμοκρασία, ΕF τo επίπεδο ενέργειας Fermi E η ενεργειακή κατάσταση ενός σωματιδίου ι και μ το συνολικό χημικό δυναμικο
Fermi- Dirac όπου k η σταθερά Boltzman, Τ η απόλυτη θερμοκρασία, ΕF τo επίπεδο ενέργειας Fermi E η ενεργειακή κατάσταση ενός σωματιδίου ι και μ το συνολικό χημικό δυναμικο