ΔΗΜΗΤΡΑ ΣΠΑΝΟΎ ΚΑΘΗΓΗΤΡΙΑ ΧΗΜΙΚΟΣ 1ου ΓΥΜΝ, ΔΑΦΝΗΣ
υπό κατασκευή
η σταθερά του ηλεκτρισμού (που εμφανίζεται π.χ. στον νόμο του Coulomb)
και η σταθερά του μαγνητισμού (που εμφανίζεται π.χ. στον υπολογισμό της έντασης του μαγνητικού πεδίου ευθύγραμμου ή κυκλικού ρευματοφόρου αγωγού)
Km = 10-7 N/A2
Ο μαθηματικός αριθμός π
Ορίζεται σαν ο λόγος της περιφέρειας προς την διάμετρο του κύκλου. Για χιλιάδες χρόονια οι μαθηματικοί προσπάθησαν να κατανοήσουν την μαθηματική και φυσική σημασία του π και να τον επεκτείνουν, εφόσον είναι ένας άρρητος αριθμός με άπειρα δεκαδικά ψηφία. Από την αρχαιότητα ο Αρχημίδης, και στον Ευρωπαικό Μεσαίωνα ο Νεύτωνας, ο Όιλερ ο Κάρλ Γκάους και άλλοι, μελέτησαν τις ιδιότητες του αριθμού π στην τριγωνομετρία, την γεωμετρία, την θερμοδυναμική, τον ηλεκτρομαγνητισμό την μηχανική. Αργότερα στα fractals
Η κατασκευή των πυραμίδων, ευρήματα στην Βαβυλωνία (1900-16 00 π.Χ.)και Αίγυπτο, αργότερα ( 600π.Χ.) στην Ινδία, στην Εβραϊκή βίβλο στην Ινδία 499μ.Χ. από τον αστρονόμο Aryabhata κ.α. μαρτυρούν την χρήση του π στους υπολογισμούς και τις κατασκευές.
Με την ανάπτυξη των απειροσειρών 16ος -17ος αιώνας και αργότερα με την ανακάλυψη του λογισμού (Νεύτων, Λαιμπνιτς), η επέκταση του π προχώρησε ακόμη περισσότερο και οδήγησε στην ανάπτυξη απείρων σειρών στην προσέγγιση του π.
Με την ανακάλυψη των υπολογιστών και αργότερα με την χρησιμοποίηση αλγορύθμων πολλαπλασιάστηκαν οι δυνατότητες υπολογισμού ακόμα περισσότερων ψηφίων του π. Όμως
(από Βικιπαίδεια) Σύμφωνα με τους Jörg Arndt και Christoph Haenel, τριάντα εννέα ψηφία είναι επαρκή να εκτελέσουν τους περισσότερους κοσμολογικούς υπολογισμούς, γιατί αυτή η ακρίβεια είναι απαραίτητη για τον υπολογισμό του όγκου του γνωστού σύμπαντος με ακρίβεια ενός ατόμου.[79
Ο αριθμός π στις Φυσικές Επιστήμες
Πολλοί φυσικοί νόμοι συμπεριλαμβάνουν το π στις μαθηματικές τους διατυπώσεις
Κυκλική συχνότητα μονάδες
Περίοδος ταλάντωσης μονάδες s
Περίοδος ηλεκτρικής ταλάντωσης LC
G : σταθερά της παγκόσμιας έλξης G = 6,673⋅10-11 Νm2 Kgr-2
{\displaystyle rad/s}
Η σταθερά του Plank
Μια θεμελιώδης φυσική σταθερά στην κβαντική μηχανική είναι η σταθερά του Plank h. Μια κοινή συντομογραφία είναι ħ = h / 2π (μειωμένη σταθερά του Plank)
-Στην θεμελιώδη εξίσωση της κυματικής έχουμε η ενέργεια να εκπέμπεται ή απορροφάται από την ύλη κατά ασυνεχή τρόπο (κβάντα ενέργειας) Η ποσότητα ενέργειας κάθε φορά είναι α Ε=hf (f είναι η συχνότητα της ακτινοβολίας)
- Οι επιτρεπόμενες τροχαιές κίνησης του ηλεκτρονίου είναι αυτές που έχουν τροχαιές στις οποίες δεν εκπέμπεται ενέργεια και έχουν στροφορμή L =nh/2π
-Η ενέργεια της θεμελιώδους στάθμης του ηλεκτρονίου είναι Eo = mee4/πmee2
- Η ακτίνα της θεμελιώδους στάθμης του ηλεκτρονίου είναι ro = h2eo/πmee2
μεταφορά από : https://en.wikipedia.org/wiki/List_of_equations_in_quantum_mechanics
Χρήση ειδικών ορων και διατάξεων για την διευκόλυνση της μαθηματικής προσέγγισης προβλημάτων
Τανυστής διανυσμάτων
Είναι γεωμετρικά αντικείμενα που μπορεί να θεωρηθούν σαν γενικευμένα διανύσματα που περιγράφουν γραμμικές σχέσεις ανάμεσα σε διανύσματα, βαθμωτα μεγέθη και άλλους τανυστές.
Παραδείγματα είναι το εσωτερικό γινόμενο, το εξωτερικό γινόμενο και ο γραμμικός μετασχηματισμός.
Οι τανυστές χρησιμοποιούνται γι να παραχθεί μαι αντιστοιχία σε σύνολα γεωμετρικών διανυσμάτων Παράδειγμα στο ηλεκτρομαγνητικό πεδίο να επιτύχουν μια συγκεκριμένη αντιστοιχία του συνόλου των εντάσεων του ηλεκτρικού και του συνόλου των διανυσμάτων της Έντασης του μαγνητικού πεδίου
Οι διαστάσεις που έχει ο τανυστής είναι τέτοιες ώστε να επιτυγχάνεται η αντιστοίχιση των αρχικών και των παραγόμενων διανυσμάτων και. ανάλογη είναι και η τάξη του .
Οι τανιστές πρέπει να είναι ανεξάρτητοι από το σύστημα συντεταγμένων. Ανάλογα σε ποιο σύστημα εφαρμόζεται ο τανιστής, προκύπτει μια οργανωμένη πολυδιάστατη συνήθως διάταξη που αντιστοιχεί στο σύστημα αυτό.
Οι τανιστές είναι σημαντικοί στη Φυσικήσε σε σε περιοχές όπως ελαστικότητα, ρευστομηχανική και γενική σχετικότητα.
Ο τελεστής αναδέλτα βαθμωτής συνάρτησης f ()
Aναδέλτα είναι διαφορικός διανυσματικός τελεστής, των μερικών παραγώγων μιας συνάρτησης ως προς τις τρεις διαστάσεις του χώρου (καρτεσιανές συντεταγμένες)
del = iθ /θx +jθ /θy +kθ /θz.
Μερικές φορές, σε διανυσματικές συναρτήσεις για χωρικές παραγώγους ( στις τρεις διαστάσεις του χώρου) χρησιμοποιείται α τελεστής ανάδελτα που είναι
H κλίση βαθμωτής συνάρτησης f grad f
Αν f βαθμωτή συνάρτηση των ανεξάρτητων μεταβλητών x, y, z . Τό
θf /θx i + θf/θy j + θf/θzk = f
H απόκλιση διανυσματικής συνάρτησης υ
Αν υ είναι διανυσματική συνάρτηση των ανεξάρτητων μεταβλητών x, y, z
θυ/θx + θυ/θy + θυ/θz = υ =divυ
Αν Δ = θ2/θx2 + θ2/θy2 + θ2/θz2 = 2
ορά (
Ανάδελτα είναι διανυσματικός διαφορικός τελεστής των μερικών παραγώγων μιας συνάρτησης ως προς τις τρεις διαστάσεις του χώρου
Εξίσωση Poisson
Γενικά η εξίσωση Poisson είναι σαν την Laplace εκτός από έναν όρο ανομοιογένειας f(x,y,z) ή εδώ ρ(r) γνωστός σαν πυκνότητα πηγής. Αν ο όρος αυτός μηδενιστεί καταλήγει στην εξίσωση laplace
Για το ηλεκτρομαγνητικό πεδίο έχουμε:
2.φ = -ρ/e0
που προκύπτει από τις δυο εξισώσεις του Ηλεκτρομαγνητισμού:
.E = ρ/e0 ( όπου ρ(r) είναι η πυκνότητα του φορτίου στην πηγή και e0 = 1/μoc2 ) και .E ==0
Από αυτήν την εξίσωση μπορεί να προκύψει το βαθμωτό δυναμικό και η ένταση του ηλεκτροστατικού πεδίου
Βρίσκει εφαρμογή και στα βαρυτικά πεδία 2.φ = 4πGρm Αν η πυκνότητα μάζας ρm είναι μηδέν τότε και αυτός καταλήγει στην εξίσωση laplace
∫ ∫αβ
Αντίστοιχα, για παράγωγα του χρόνου χρησιμοποιείται τα
https://el.wikipedia.org/wiki/Ανάδελτα)
σταθερά του ηλεκτρισμού (που εμφανίζεται π.χ. στον νόμο του Coulomb)
και η σταθερά του μαγνητισμού (που εμφανίζεται π.χ. στον υπολογισμό της έντασης του μαγνητικού πεδίου ευθύγραμμου ή κυκλικού ρευματοφόρου αγωγού)
Km = 10-7 N/A2

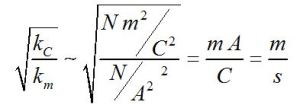
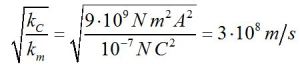


 μονάδες s
μονάδες s )
)
