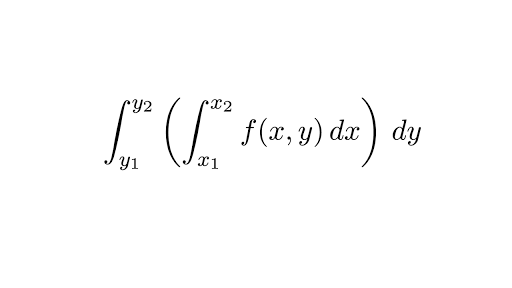Αρχική Σελίδα > Τα μαθηματικά στις Φυσικές Επιστήμες. H έννοια του Λογισμού στα Μαθηματικά με τους δυο Κλάδους του: Διαφορικός και Ολοκληρωτικός , για υπολογισμούς σε διαρκείς μεταβολές και συνολικών ποσοτήτων. Ολοκληρωτικός Λογισμός:

Τα μαθηματικά στις Φυσικές Επιστήμες. H έννοια του Λογισμού στα Μαθηματικά με τους δυο Κλάδους του: Διαφορικός και Ολοκληρωτικός , για υπολογισμούς σε διαρκείς μεταβολές και συνολικών ποσοτήτων. Ολοκληρωτικός Λογισμός:

ΔΗΜΗΤΡΑ ΣΠΑΝΟΎ ΚΑΘΗΓΗΤΡΙΑ ΧΗΜΙΚΟΣ 1ου ΓΥΜΝ, ΔΑΦΝΗΣ

υπό κατασκευή

O Λογισμός στα Μαθηματικά περιγράφει διαρκείς μεταβολές

Αρχικά οι υπολογισμοί στα διάφορα μεγέθη γίονταν για συγκεκριμένες καταστάσεις. Στην πραγματικότητα όμως οι καταστάσεις αυτές μεταβάλονται συνεχώς και τα αποτελέσματα των υπολογισμών μας αλλάζουν . Ο Λογισμός είναι ένας κλάδος των Μαθηματικών που επιτυγχάνει να έχει διαρκή αποτελέσματα κατά την διάρκεια των μεταβολών αυτών, είτε όσον αφορά τον τρόπο που γίνονται (κλίσεις καμπυλών στον διαφορικό λογισμό) ή τον υπολογισμό των συνολικών ποσοτήτων που παράγονται κατά την διάρκεια των μεταβολών αυτών με τον ολοκληρωτικό λογισμό

Ο λογισμός έχει εφαρμογές στις επιστήμες, οικονομία, μηχανική και άλλα.

Ο ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ

Έχει θέμα του την μελέτη του αόριστου και του ορισμένου ολοκληρώματος και τις εφαρμογές τους

Το αόριστο ολοκλήρωμα είναι αντιπαράγωγος. Η αντίστροφη λειτουργία της παραγώγου. Αν έχουμε την συνάρτηση f η ολοκλήρωσή της δίνει μια νέα συνάρτηση F η οποία αν παραγωτοποιηθεί θα δώσει την αρχική f. Το σύμβολο της αόριστης ολοκλήρωσης είναι $\int \,$

Για συναρτήσεις δύο μεταβλητών, το ορισμένο ολοκλήρωμα, εισάγει μια συνάρτηση που παράγει έναν αριθμό ώστε να υπολογισθεί το άθροισμα των εμβαδών μεταξύ της καμπύλης της γραφικής παράστασης της εισόδου και του άξονα χ

Υπολογισμός εμβαδού επίπεδης περιοχής με ολοκλήρωμα

A. Έστω f:[a, b] συνάρτηση φραγμένη. με τιμές στο R

Aν θέλουμε να υπολογίσουμε το εμβαδόν Ε που περικλείεται από τα a, b, [a, b] και την καμπύλη της συνάρτησης, θα πρέπει να διαμερίσουμε το [a ,b] σε υποδιασήματα (dx), να πολλάπλασιάσουμε κάθε ένα από αυτά με το αντίστοιχο y και να τα αθροίσουμε . Αποδεικνύεται πως,

Το ορισμένο ολοκλήρωμα που γράφεται : $\int _{a}^{b}f(x)\,dx.$

είναι επίσης ίσο με το εμβαδόν Ε και ισχύει ότι: $\int _{\alpha }^{\beta }f(t)\,dt=F(\beta )-F(\alpha ).$ (θεώρημα κλίσης)

B. Αν το ζητούμενο εμβαδόν περικλείεται μεταξύ δύο συναρτήσεων f και g συνεχείς στο κλειστό διάστημα [a,b] ώστε να ισχύει f(x) >g(x) για κάθε x του διαστήματος [α,β] τό εμβαδό που περικλείεται από τις γραφικές παραστάσεις f και g και τις κατακόρυφες ευθείες a και b είναι

Αν έχουμε συνάρτηση g(x)

συνεχείς στο κλειστό διάστημα [a,b] ώστε να ισχύει 0 >g(x) τότε ισχύει:

Γ. Αν έχω συνάρτηση f(x) και θέλω να υπολογίσω το εμβαδόν του χωρίου Ω που περικλείεται από τον άξονα x'x, τη γραφική παράσταση μιας συνάρτησης f, με f(x) > 0 για κάθε x ϵ [α,β]

Θεωρώ την ευθεία xx΄ σαν g(x) =0 άρα από την προηγούμενη περίπτωση έχω Ε(Ω) = $\int _{a}^{b}f(x)\,dx.$

Απεικόνιση όγκου με τα διπλά ολοκληρώματα

$\int \,$ $\int \,$ f(x,y) dxdy Είναι ενα διπλό ολοκλήρωμα μεταξύ [a, b] και [c ,d] παριστάνει όγκο στερεού που έχει βάσεις το [α,β] . [c.d] και το υψος προκύπτει από τα ενδιάμεσα παραλληλεπίπεδα

Έστω f:[a, b] συνεχής συνάρτηση και φραγμένη. με τιμές στο R και f(x) >η ίσο από το 0 για κάθε του [a, b]

Aν θεωρήσουμε

εμβαδόν του χωρίου Ω που περικλείεται από τη γραφική παράσταση της g(x) =( α-x² )+ β και τον άξονα x'x

και εφόσον g(x) =0 (ο άξονας xx΄)

Image result for volume of the solid, produced by rotating around from the '0' axis όπου Ο όγκος που παράγεται με την περιστροφή της περιοχής Ω γύρω από τον x΄0x δίνεται από το σχήμα και είναι :

Image result for double integers volume diagrammes

Επικαμπύλια ολοκληρώματα

Χρησιμοποιούνται ευρέως στην Φυσική και στις επιστήμες του μηχανικού.

Όταν πρόκειται για μια απλή προσανατολισμένη καμπύλη που περικλείει ένα χωρίο στο R² χρησιμοποιείται το επικαμπύλιο ολοκλήρωμα πάνω στην C

Av C αποτελεί το για μια απλή προσανατολισμένη καμπύλη που περικλείει ένα χωρίο στο R

ΠΗΓΕΣ

https://ebooks.edu.gr/modules/ebook/show.php/DSGL-C105/492/3199,13000/

https://thalis.math.upatras.gr/~tsoubeli/MDEI.pdf

το θεωρητικό λογισμό, το θεώρημα απόκλισης, γνωστό και ως θεώρημα του Gauss ή το θεώρημα του Ostrogradsky [1], είναι ένα αποτέλεσμα που συνδέει τη ροή (δηλαδή ροή) ενός πεδίου διανύσματος μέσω μιας επιφάνειας με τη συμπεριφορά του πεδίου τανυστή μέσα στην επιφάνεια .

Πιο συγκεκριμένα, το θεώρημα απόκλισης δηλώνει ότι η προς τα έξω ροή ενός πεδίου τάσης μέσω μιας κλειστής επιφάνειας είναι ίση με το ολοκλήρωμα όγκου της απόκλισης πάνω στην περιοχή μέσα στην επιφάνεια. Διαισθητικά, δηλώνει ότι το άθροισμα όλων των πηγών (με τους νεροχύτες που θεωρούνται ως αρνητικές πηγές) δίνει την καθαρή ροή έξω από μια περιοχή.

Το θεώρημα απόκλισης είναι ένα σημαντικό αποτέλεσμα για τα μαθηματικά της φυσικής και της μηχανικής, ιδιαίτερα στην ηλεκτροστατική και τη δυναμική των ρευστών.

Στη φυσική και στη μηχανική, το θεώρημα απόκλισης εφαρμόζεται συνήθως σε τρεις διαστάσεις. Ωστόσο, γενικεύει σε οποιοδήποτε αριθμό διαστάσεων. Σε μια διάσταση, είναι ισοδύναμο με το θεμελιώδες θεώρημα του λογισμού. Σε δύο διαστάσεις, είναι ισοδύναμο με το θεώρημα του Green.

ΠΗΓΕΣ

https://el.wikipedia.org/wiki/%CE%9B%CE%BF%CE%B3%CE%B9%CF%83%CE%BC%CF%8C%CF%82#%CE%9F%CE%BB%CE%BF%CE%BA%CE%BB%CE%B7%CF%81%CF%89%CF%84%CE%B9%CE%BA%CF%8C%CF%82_%CE%9B%CE%BF%CE%B3%CE%B9%CF%83%CE%BC%CF%8C%CF%82

Κλίση συνάρτησης - Βικιπαίδεια

Βικιπαίδει

https://ebooks.edu.gr/modules/ebook/show.php/DSGL-C105/492/3197,12978/

ακατεργαστο

ΘΕΩΡΗΜΑ ΤΗΣ ΑΠΟΚΛΙΣΗΣ

Πιο συγκεκριμένα, το θεώρημα απόκλισης δηλώνει ότι η προς τα έξω ροή ενός πεδίου τάσης μέσω μιας κλειστής επιφάνειας είναι ίση με το ολοκλήρωμα όγκου της απόκλισης πάνω στην περιοχή μέσα στην επιφάνεια. ... Σε μια διάσταση, είναι ισοδύναμη με το θεμελιώδες θεώρημα του λογισμού.

Ένα πεδίο εφρμογής του Ολοκληρωτικού λογισμού είναι

σχέση ισοδυναμίας μεταξύ μιας οποιαδήποτε ροής, όπως ενός υγρού, της ηλεκτρικής ή της βαρυτικής, που ρέει έξω από μια οποιαδήποτε κλειστή επιφάνεια και το αποτέλεσμα των εσωτερικών πηγών, όπως το ηλεκτρικό φορτίο ή η μάζα, που περιέχονται στον όγκο που περικλείει η επιφάνεια.

Επικαμπύλια ολοκληρώματα. Διπλά και τριπλά ολοκληρώματα και εφαρμογές στη Φυσική και τη Γεωμετρία: υπολογισμός όγκων, ροπών αδράνειας, εμβαδών επιφανειών. Επιφανειακά ολοκληρώματα και εφαρμογές στη ροή των ρευστών. Το Θεώρημα του Green. Παραμετρική αναπαράσταση επιφανειών και εφαρμογές. Το Θεώρημα του Stokes και εφαρμογές στη Φυσική. Το Θεώρημα της Απόκλισης.

$\Phi_B = \oint_S \mathbf{B} \cdot \mathrm{d}\mathbf{A} = 0$
Ηλεκτρισμός · Μαγνητισμός

Παρατήρηση 2.5.

Η αρχή του Hamilton ορίζει ότι από όλες τις πιθανές κινήσεις στον χώρο το σώμα επιλέγει να κινηθεί σε αυτήν για την οποία το έχει ελάχιστη τιμή. Αυτό μας παραπέμπει κατευθείαν στον λογισμό μεταβολών. Άρα μπορούμε αμέσως να δούμε ότι η αρχή του Hamilton διατυπώνεται και ως (δείτε την Εξ. (2.89))

\delta I=\delta\int_{t_{1}}^{t_{2}}L(q_{1},\ldots,q_{n},\dot{q}_{1},\ldots,% \dot{q}_{n},t)\,dt=0,

(2.41)

όπου το σύμβολο δηλώνει τη μεταβολή του .

2.2.3 Ολοκλήρωμα δράσης

Το ολοκλήρωμα (2.40), του οποίου η ολοκληρωταία ποσότητα είναι η Λαγκρανζιανή και η ολοκλήρωση είναι στον χρόνο, λέγεται ολοκλήρωμα δράσης (τέτοια ολοκληρώματα μελετώνται στο υποκεφάλαιο 2.3). Το είναι ένα συναρτησιακό όπου τον ρόλο του παίζει ο χρόνος . Πρέπει όμως να προσέξουμε ότι το εξαρτάται από συναρτήσεις και όχι από μία μόνο συνάρτηση όπως το στην Εξ. (2.79).

Ζητάμε ελάχιστα του ολοκληρώματος δράσης (2.40). Θα θέλαμε δηλαδή τις συνθήκες για τις οποίες η μεταβολή είναι μηδέν, όπως στην Εξ. (2.41) και συνεπώς ζητάμε μία γενίκευση του αποτελέσματος (2.97) το οποίο δίνει τις εξισώσεις Euler-Lagrange για συναρτησιακό το οποίο εξαρτάται από μία μόνο συνάρτηση.

Η γενίκευση θα δίνει εξισώσεις Euler-Lagrange για συναρτησιακό το οποίο εξαρτάται από συναρτήσεις . Από τη συνθήκη προκύπτουν οι εξής εξισώσεις Euler-Lagrange

ÎÏÎ¿ÏÎÎ»ÎµÏÎ¼Î± ÎµÎ¹ÎºÏÎ½Î±Ï Î³Î¹Î± maxwell equations

Παρατήρηση 2.5.

2.2.3 Ολοκλήρωμα δράσης

Επαφή