ΔΗΜΗΤΡΑ ΣΠΑΝΟΎ ΚΑΘΗΓΗΤΡΙΑ ΧΗΜΙΚΟΣ 1ου ΓΥΜΝ, ΔΑΦΝΗΣ
υπό κατασκευή
O Λογισμός στα Μαθηματικά περιγράφει διαρκείς μεταβολές
Αρχικά οι υπολογισμοί στα διάφορα μεγέθη γίονταν για συγκεκριμένες καταστάσεις. Στην πραγματικότητα όμως οι καταστάσεις αυτές μεταβάλονται συνεχώς και τα αποτελέσματα των υπολογισμών μας αλλάζουν . Ο Λογισμός είναι ένας κλάδος των Μαθηματικών που επιτυγχάνει να έχει διαρκή αποτελέσματα κατά την διάρκεια των μεταβολών αυτών, είτε όσον αφορά τον τρόπο που γίνονται (κλίσεις καμπυλών στον διαφορικό λογισμό) ή τον υπολογισμό των συνολικών ποσοτήτων που παράγονται κατά την διάρκεια των μεταβολών αυτών με τον ολοκληρωτικό λογισμό
Ο λογισμός έχει εφαρμογές στις επιστήμες, οικονομία, μηχανική και άλλα.
ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ
Ο διαφορικός Λογισμός και οι διαφορικές εξισώσεις χρησιμοποιούνται για την επίλυση προβλημάτων κίνησης, γεωμετρίας, μηχανικής κ.α.
Η έννοια της παραγώγου
Υπάρχουν μεγέθη στις επιστήμες αυτές των η τιμή εξαρτάται από άλλα μεγέθη. μ= μ(λ).
Η παράγωγος dμ/dλ είναι συντελεστής μεταβολής που δίνει πόσο γρήγορα μεταβάλλεται το μέγεθος μ σε σχέση με το μέγεθος λ. Χρησιμοποιούμε τότε απλές ή σύνηθεις διαφορικές εξισώσεις
Αν το μέγεθος μ εξαρτάται από δύο ή και περισσότερα μεγέθη μιλάμε τότε για μερικές παραγώγους.
 Αν υπάρχει συνάρτηση f(x) , με πεδίο ορισμού S που ανήκει στο R
Αν υπάρχει συνάρτηση f(x) , με πεδίο ορισμού S που ανήκει στο R
τότε
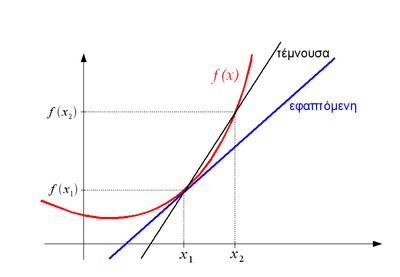
η παράγωγος αυτής της συνάρτησης f΄ στο σημείο Α (xo, f(xo) ), δίνεται αν θεωρήσουμε τον λόγο f(x )-f(x0) /x-x0 ) που είναι η κλίση τέμνουσας ΑΜ [Α (x0, f(x0)) M (x, f(x))]
και μετά, πάρουμε το όριο
 |
,Στο όριο αυτό, η τέμνουσα γίνεται εφαπτώμενη στο Α (x0, f(x0))
Αν αυτό το όριο υπάρχει και έχει πραγματική τιμή λέμε ότι η συνάρτηση είναι διαφοροποιήσιμη στο Α .
Η ποσότητα που προκύπτει ) ονομάζεται παράγωγος f΄της f στο σημείο Α . Για να γίνει αυτό πρέπει η f να είναι συνεχής στο σημείο Α.
Θυμίζουμε ποιες κατηγορίες συναρτήσεων είναι συνεχείς:
Πολυωνυμικές συναρτήσεις (στο R)
Ρητές συναρτήσεις P/Q.
Οι συναρτήσεις f(x) =ημx και g(x) =συνx
Αν η f είναι συνεχής στο πεδίο ορισμού της και διαφοροποιήσιμη, δηλαδή
Εάν υπάρχει αντίστοιχη παράγωγος f΄για κάθε σημείο του πεδίου ορισμού της συνάρτησης f, με αντίστοιχο πεδίο ορισμού της ένα υποσύνολο του S
τότε μπορούμε να πούμε πως η παράγωγος της f(x) είναι και αυτή συνάρτηση , είναι η f΄(x). Η παραγώγηση γίνεται βάσει νόμων που φαίνονται στον κάτω πίνακα
 |
H f΄ (x) μπορεί να εκπληρεί τις προυποθέσεις για παραγώγηση τότε με αντίστοιχο τρόπο μπορούμε να πάρουμε την δεύτερη παράγωγο f΄΄(x)
και αντίστοιχα και τις επόμενες τρίτη , τέταρτη κ.λ.π.
Η εξίσωση της εφαπτώμενης είναι y − f(x0) = f ʹ(x0) (x − x0)
Σχετικά με την λύση μιας διαφορικής εξίσωσης. Γενική λύση,
Υπάρχουν πολλοί τρόποι επίλυσης των διαφορικών εξισώσεων που ταξινομούνται σε διάφορες κατηγορίες. Εδώ θα δώσουμε πιο μεγάλη βαρύτητα με όσες συνδέονται με προβλήματα Φυσικών Επιστημών κυρίως, τέτοιων ώστε να είναι δυνατή η αναφορά και η κατανόησή τους στο παρόν άρθρο.
Οι φυσικοί που επιχειρούν να επεξεργαστούν τα θέματά τους με την βοήθεια των μαθηματικών, έχουν σαν πρώτο καθήκον τους να μεταφέρουν στον κόσμο των μαθηματικών και του διαφορικού λογισμού τα δεδομένα τους. Εξαρτάται από την περίπτωση αν η μαθηματική διατύπωση των θεωριών και των προβλημάτων των Φυσικών Επιστημών μπορεί να επιλυθεί άμεσα από τους ίδιους τους Φυσικούς ή στην συνέχεια με την αρωγή των μαθηματικών συναδέλφων τους με καθαρά μαθηματικές διαδικασίες ,. Σε παλαιότερες εποχές του Newton (1642-1727) και του Leibniz (1646-1716). οι τότε μαθηματικοί είχαν επαρκείς γνώσεις και Φυσικής ώστε να διατυπώνουν και να επιλύουν ΔΕ.
κατέγραψε φαινόμενα Ροικής κίνησης με εξισώσεις διαφορικού λογισμού, τις οποίες επέλυσε ο Lei
Γενικά όμως
Η επίλυση μιας διαφορικής εξίσωσης είναι μια άλλη συνάρτηση που ικανοποιεί εκ ταυτότητος την διαφορική εξίσωση δηλαδή για κάθε χ.
Μερικές από αυτές έχουν ήδη επιλυθεί, ενώ άλλες χρειάζονται λογισμικό ηλεκτρονικών υπολογιστών για να δώσουν λύση.
Ένα παράδειγμα διαφορικής εξίσωσης είναι η:
y′+2xy- e−x2 =0 (1) που είναι 1ης τάξης έχει λύση τη y=xe−x2 (2) .
Αν αντικαταστήσουμε την ( 2) στην (1), η(1) επαληθεύεται για κάθε x.
H Διαφορική εξίσωση έχει άπειρες λυσεις. Για κάθε x έχω και μια διαφορετική λύση. Για να
Αν αντί του x θέσω x+c , όπου c αυθαίρετη σταθερά, ώστε η λύση (2) γίνει y=(x + c)e−x2 *(3)
η (3) είναι επίσης λύση και επαληθεύει την (1). και ονομάζεται γενική λύση της (1)

Αν στην c δώσουμε διάφορες τιμές οι συναρτεις- λύσεις που προκύπτουν ονομάζονται μερικές λύσεις.
Κάθε μερική λύση είναι η εφαπτώμενη σε ένα σημείο της γραφικής παράστασης της αρχικής ΔΕ
- Ο αριθμός των σταθερών c που προκύπτουν είναι ίδιος με την τάξη της συνάρτησης.
- Αν υπάρχει μια συνάρτηση με n σταθερές που επαληθεύει εκ ταυτότητας μια Διαφορική Εξίσωση n τάξης τότε είναι η γενική λύση της
Μiα πολύ απλή και σύνηθης ΔΕ η dy/dx= ay έχει λύση y(x)=ceax
Στην ίδια ΔΕ dy/dx= ay, βασίζεται και η επίλυση πολλών προβλημάτων εκπομπής ραδιενεργού ακτινοβολίας, πριβλήματα ανατοκισμού , πληθυσμιακές δυναμικές για την βιολογία αλλα και την δημογραφία, κ.α.
Ανάλυση της Διαφορικής εξίσωσης
Σε μια τέτοια λύση μπορούμε να αναλύσουμε περισσότερο τις τιμές που μπορεί να δώσει ανάλογα με το c kai τo a
αν a>0 το όριο της f(x) είναι το άπειρο αν το c >0 και το μείον άπειρο
αν c<0. Αν a>0 το όριο της f(x) είναι το 0 .
Αν a=0 τότε f(x)=c (σταθερά)
Τάξη, βαθμός, λύση της διαφορικής εξίσωσης
Τάξη μιας διαφορικής εξίσωσης είναι η μεγαλύτερη τάξη παραγώγου της άγνωστης συνάρτησης που εμφανίζεται στην εξίσωση π.χ. d2y/dx =2xdydx είναι δευτέρας τάξης
Βαθμός μιας διαφορικής εξίσωσης είναι η δύναμη στην οποία είναι υψωμένη η παράγωγος της μεγαλύτερης τάξης, αφού γίνει απαλειφή τυχόν δυνάμεων και τα μέλη της εξίσωσης γραφούν σαν πολυώνυμα συναρτήσεων και των παραγώγων τους. Παράδειγμα η παρακάτω διαφορική εξίσωση είναι 2ης τάξης και 1ου βαθμού ,

Ολοκληρωτικές καμπύλες μιας Διαφορικής Εξίσωσης
Είναι οι γραφικές παραστάσεις των μερικών λύσεων μιας Διαφορικής Εξίσωσης. Πρόκειται για παραμετρικές καμπύλες που αντιπροσωπεύουν μια συγκεκριμένη λύση μια διαφορική εξίσωση ή σε ένα σύστημα εξισώσεων. Είναι γνωστές και με άλλα ονόματα όπως για παράδειγμα στην Φυσική στον ηλεκτρομαγνητισμό είναι γνωστές σαν γραμμές πεδίου στην κίνηση πάνω στην γήινη σφαίρα σαν μεσημβρινοί και παράλληλοι ή στην ροή ρευστού σαν ολοκληρωμένες καμπύλες για το πεδίο ταχύτητας ρευστού (streemlines)
Στο μαθηματικό διάγραμμα έχουμε τις ολοκληρωμένες καμπύλες της ΔΕ: dy / dx = x2 − x − 2. που δίνουν την κάθε ομάδα των διαφορικών καμπυλών
και
Δεύτερο παράδειγμα η ΔΕ (y΄)2 -4y=0 . που έχει γενική λύση y=(x+c)2 που δίνει μια οικογένεια καμπυλών με ελάχιστο το xo=-c
Ενώ στην συνέχεια τις δυναμικές γραμμές ενός ηλεκτρικού πεδίου, της οι γεωγραφικές συντεταγμένες που δίνουν την κίνηση στην επιφάνεις της γήινης σφαίρας και της καμπύλες για την ταχύτητα ροής ρευστού. Εννοείται ότι σε αντίστοιχες θεωρίες που εκφράζονται μέσα από διαφορικές εξισώσεις των οποίων οι γενικές λύσεις δίνουν σύνολα ολοκληρωτικών καμπυλών.


Σημείωση: Εκτός από τις λύσεις της ΔΕ που προκύπτουν από την γενική λύση υπάρχουν κάποιες φορές άλλες που δεν προκύπτουν από την γενική λύση και ονομάζονται ιδιάζουσες.
Περιβάλλουσα συνάρτηση:
Σε κάποιες περιπτώσεις σε μια οικογένεια ολοκληρωτικών καμπυλών που προκύπτουν από τη γενική λύση υπάρχει μια καμπύλη που περιβάλει αυτές και
όλες οι άλλες ολοκληρωτικές καμπύλες της οικογένειας καμπυλών εφάπτονται σε αυτήν. Ίσχύει επίσης ότι σε κάθε σημείο της περιβάλλουσας καμπύλης εφάπτεται και μια εκ των ολοκληρωτικών καμπυλών. Η κλιση της περιβάλλουσας δίνεται από την σχέση ,
 είναι η παράγωγος ως προς την σταθερά c
είναι η παράγωγος ως προς την σταθερά c
y΄περ = y΄c/ x΄
Τα όρια συνάρτησης στις διαφορικές εξισώσεις
Σε ορισμένες περιπτώσεις, η αρχική διαφορική εξίσωση αναφέρεται για απειροελέχιστες μεταβολές , όπως για παράδειγμα στην στιγμιαία ταχύτητα ή την επιτάχυνση μεταβαλλόμενης κίνησης. Εδώ βέβαια και εφόσον χρησιμοποιούμε απειροελάχιστες μεταβολές χρειαζόμαστε και την χρήση των ορίων για την για την ακριβέστερη διατύπωση

