Τα μαθηματικά στις Φυσικές Επιστήμες: Οι αριθμοί, οι πραγματικοί αριθμοί, οι φανταστικοί αριθμοί και οι μιγαδικοί αριθμο στην Φυσική. Οι συναρτήσεις , πραγματικές, μιγαδικές, διαφορικές, διανυσματικές,

της Δήμητρας Σπανού 

υπό κατασκευή

ΟΙ ΑΡΙΘΜΟΙ 

Οι φυσικοί αριθμοί   1,2,3,...είναι αφηρημένες έννοιες που περιγράφουν μέγεθος συνόλων

Οι ακέραιοι αριθμοί   0,1,2,3,...είναι αφηρημένες έννοιες που περιγράφουν τα σχετικά  μεγέθη συνόλων (πόσα παραπάνω έχει το Α από το Β)

Οι ρητοί αριθμοί   1,2,3,...είναι αφηρημένες έννοιες που περιγράφουν λόγους μεγεθών 2 συνόλων. Αν πήρα τα 3/4 από ένα σύνολο,  αυτό έχει 4 μέρη (το πρώτο σύνολο) κι εγώ πήρα τα 3 (σύνολο αυτών που πήρα)

ΠΡΑΓΜΑΤΙΚΟΤΗΤΑ ΚΑΙ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ 

ΓΙΑ ΠΕΡΙΓΡΑΦΗ ΘΕΜΑΤΩΝ ΚΛΑΣΣΙΚΗΣ ΦΥΣΙΚΗΣ

Οι πραγματικοί αριθμοί εξυπηρέτησαν για πολλά χρόνια τις Φυσικές Επιστήμες και έως τις αρχές του 20ου αιώνα δεν υπήρξε καμμιά απαιτηση για την ανάγκη εισαγωγής άλλου συστήματος στην Φυσική .

Το σύστημα των πραγματικών αριθμών έχει επιλεγεί στην φυσική για την "μαθηματική του λειτουργικότητα, απλότητα, κομψότητα, σε συνδυασμό με το γεγονός ότι βρίσκεται σε συμφωνία με τις φυσικές έννοιες της απόστασης και του χρόνου σε πολύ μεγάλη περιοχή τιμών

Μας προδιαθέτει ακόμα ότι αυτή η συμφωνία παύει να υπάρχει σε πολύ μικρές τάξεις μεγέθους για την απόσταση ή τον χρόνο

Οι πραγματικοί αριθμοί μπορούν να περιγράψουν ικανοποιητικά τα θέματα της Κλασσικής Φυσικής. Επί πλέον βρίσκονται σε συμφωνία με τις φυσικές έννοιες της απόστασης και του χρόνου. 

Πέντε είναι οι βασικοί νόμοι της φύσης όπου μπορούν να χρησιμοποιηθούν οι πραγματικοί αριθμοί των μαθηματικών για τους υπολογισμούς Φυσικών μεγεθών 

Η εξίσωση για την Μελέτη της κίνησης των μαζών σε πεδία δυνάμεων και οι 4 εξισώσεις του Maxwell

Οι πραγματικοί αριθμοί  C ή R1 έχουν προέλθει από τους φυσικούς αριθμούς (Ν αγγλική λέξη Natural) που προσδιορίζει μια ασυνεχή οντότητα (π.χ. δέκα ποτήρια). Από αυτό προήλθε το σόνολοτων ακεραίων Ζ από τη γερμανική λέξη Zahl μέσα από την πράξη της αφαίρεσης των  φυσικών και των ρητών Q (από τη αγγλική λέξη Quotient που σημαίνει πηλίκο) 

Oi πραγματικοί αριθμοί είναι αφηρημένες έννοιες που περιγράφουν τα μέτρα συνεχών ποσοτήτων (όπως μήκος, βάρος , ποσότητα μάζας κ.α.)

Οι μιγαδικοί αριθμοί είναι διατεταγμένα ζεύγη πραγματικών αριθμών με την προσθήκη ενός ακόμα στοιχείου της τετραγωνικής ρίζας του-1

Οι μιγαδικοί αριθμοί εισάγωνται στην επιστήμη των μααθηματικών τον 16ο αιώνα από τον Ιταλό Ρενέ Ντεκαρτ,

  λόγω της ανάγκης για  ευρεσης τετραγωνικής ρίζας του -1

Είναι επέκταση των πραγματικών αριθμών με την προσθήκη ενός στοιχείου του i ώστε i² = -1 

Έτσι, δημιουργείται ένας νέος αριθμός που χαρακτηρίστηκε  «imaginaire» δηλαδή «φανταστικός»- και απέκτησε δικό του συμβολισμό  i

τον 18ο αιώνα από πρόταση  του μαθηματικού EULER στο γνωστό βιβλίο του Elements of Algebra ως ‘neither nothing, nor greater than nothing, nor less than nothing… (ούτε τίποτε, ούτε μεγαλύτερο από το τίποτε, ούτε μικρότερο από το τίποτε!) 

Ακόμα ο Euler και οι μαθηματικοί τη εποχής εκείνης είπαν ότι οι φανταστικοί αριθμοί εφευρέθηκαν δεν επινοήθηκαν.

these numbers present themselves to the mind; they exist in our imagination and we still have a sufficient idea of them

Αυτοί οι αριθμοί παρουσιάζονται στον μυαλό. υπάρχουν στη φαντασία μας και έχουμε ακόμα μια επαρκή ιδέα γι 'αυτούς

Η ένωση των φανταστικών με τους πραγματικούς αριθμούς απετέλεσε το σύνολο των μιγαδικών αριθμών Ζ που έμελλε να παίξει πρωταρχικό ρόλο στην εξέλιξη των φυσικών επιστημών αλλά και της  ιστορίας γενικά.

${\displaystyle a+ib}$

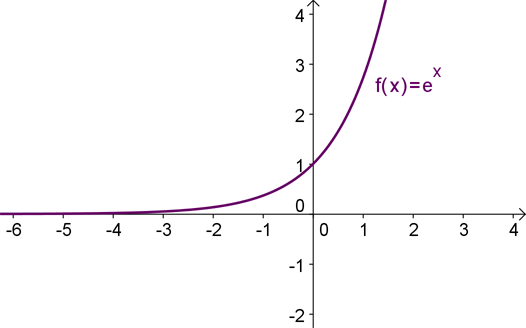
ΟΙ ΣΥΝΑΡΤΗΣΕΙΣ Στα Μαθηματικά , συνάρτηση ή απεικόνιση είναι μια αντιστοίχιση μεταξύ δύο συνόλων, που καλούνται   πεδίο ορισμούA και πεδίο τιμών B.    Κάθε ένα στοιχείο απο το πεδίο ορισμού Α πρέπει να αντιστοιχίζεται σε ένα και μόνο στοιχείο του πεδίου τιμών Β.    Συναρτήσεις που ορίζονται στο σύνολο των πραγματικών αριθμών καλούνται πραγματικές συναρτήσεις    Όταν κάθε συνάρτηση f: A→B με Α⊆R      και Β⊆R και η απεικόνησή τους  με Α⊆R     γίνεται  στο καρτεσιανό επίπεδο με ζευγάρια αριθμών  (x, f(x) που αντιστοιχούν σε σημεία του επιπέδου  γραφική παράσταση είναι η απεικόνιση αυτών των ζευγαριών στο καρτεσιανό επίπεδο, όπου κάθε ζευγάρι ορίσματος-τιμής είναι ένα σημείο της γραφικής παράστασης και το σύνολο των σημείων σχηματίζουν τη καμπύλη της γραφικής παράστασης.   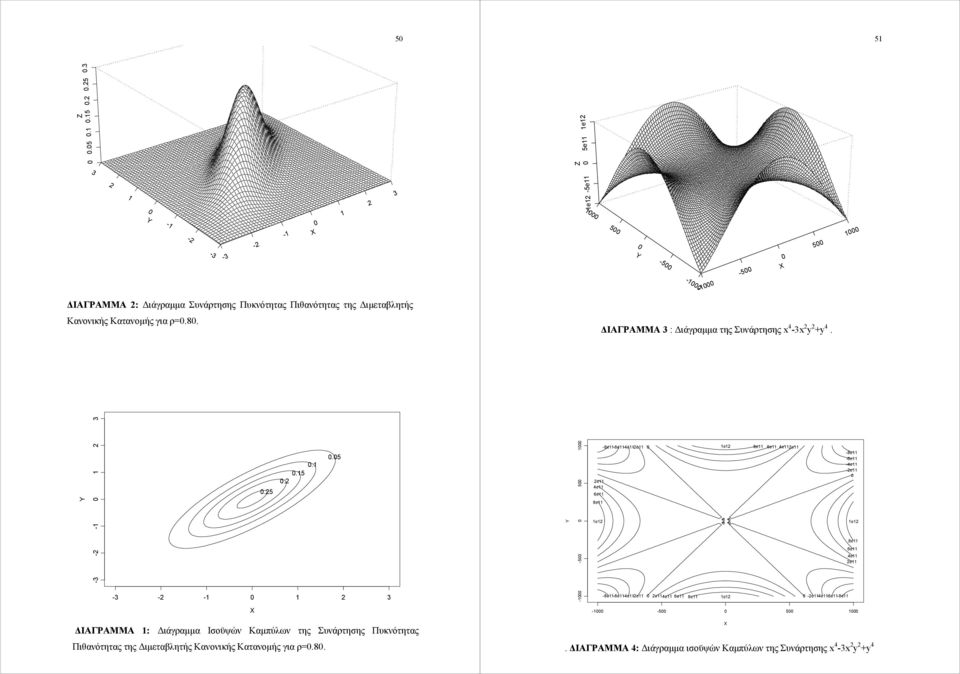Πραγματικες συναρτήσεις n μεταβλητών Oi συναρτήσεις μπορεί να έχουν και περισσότερες από μια μεταβλητές Κάθε συνάρτηση f: A→B με Α⊆Rn και Β⊆Rn   ονομάζεται πραγματική συνάρτηση n μεταβλητών. Για n=2 η γραφική παράσταση είναι τρισδιάστατη (μήκος, πλάτος και ύψος).  Εναλλακτική απεικόνιση γίνεται με τα διαγράμματα ισοϋψών καμπύλων (contour plots)  (μεταφορά από https://www2.stat-athens.aueb.gr/~jbn/courses/maths/math_notes/maths4.pdf)     Μιγαδικές  συναρτήσεις Το σύνολο των μιγαδικών αριθμών αποτελείται από συνθετους αριθμούς, αριθμούς- διατεταγμένα ζεύγη ( ) Μια σύνθετη συνάρτηση είναι  από σύνθετους αριθμούς σε σύνθετους αριθμούς Φυσιολογικά ορίζεται ένας τομέας που είναι ανοικτό υποσύνολο του επιπέδου των μιγαδικών αριθμών Ζ Κάθε τέτοια πολύπλοκη συνάρτηση, λαμβάνει τιμές z από τον τομέα αυτόν και οι εικόνες τους f(z) ανήκουν επίσης στους μιγαδικούς αριθμούς. Μια μιγαδική συνάρτηση  μπορεί να χωριστεί σε πραγματικά και φανταστικά μέρη   z=a + bi      και  f(z) = f(a+bi) = u(a,b)  + iv(a,b)    όπου z, f(z), a, b, u,v είναι πραγματικοί αριθμοί   Διαφορικές Συναρτήσεις. Μιας μεταβλητής (σύνηθεις) ή περισσότερων (μερικές) Είναι συναρτήσεις μιας ή περισσότερων μεταβλητών που περιέχουν μια ή περισσότερες μεταβλητές και παραγώγους τους. Μπορεί να έχουν μια μεταβλητή (σύνηθεις Δ.Ε.) ή περισσότερες (μερικές Δ.Ε,) Μια μερική διαφορική εξίσωση με δύο μεταβλητές έχει τρεις παραγώγους και μπορεί να γραφεί με γενικό τύπο Αθ2 Ψ/θx2 +Βθ2Ψ/θyθx+Cθ2Ψ/θy2 ) + D(x,y,Ψ, θΨ/θx, θΨ/θy)         Διανυσματικές συναρτήσεις ⊆  ΠΗΓΕΣ   https://el.wikipedia.org/wiki/Μιγαδικός_αριθμός https://el.wikipedia.org/wiki/Φανταστικός_αριθμός   ${\displaystyle {\textit {Bi}}={\frac {hL}{k}}}$           όπ;oου z,                         This last equation is in a very high dimension,[2] so the solutions are not easy to visualize. ${\displaystyle \Psi =\Psi (\mathbf {r} ,t)}$ ${\displaystyle \Psi =\Psi (\mathbf {r} _{1},\mathbf {r} _{2},\cdots \mathbf {r} _{N},t)}$ Photoemission[edit] Property/Effect Nomenclature Equation Photoelectric equation Kmax = Maximum kinetic energy of ejected electron (J) h = Planck's constant f = frequency of incident photons (Hz = s−1) φ, Φ = Work function of the material the photons are incident on (J) ${\displaystyle K_{\mathrm {max} }=hf-\Phi \,\!}$ Threshold frequency and φ, Φ = Work function of the material the photons are incident on (J) f0, ν0 = Threshold frequency (Hz = s−1) Can only be found by experiment. The De Broglie relations give the relation between them: ${\displaystyle \phi =hf_{0}\,\!}$ Photon momentum p = momentum of photon (kg m s−1) f = frequency of photon (Hz = s−1) λ = wavelength of photon (m) The De Broglie relations give: ${\displaystyle p=hf/c=h/\lambda \,\!}$ Quantum uncertainty[edit] Property or effect Nomenclature Equation Heisenberg's uncertainty principles n = number of photons φ = wave phase [, ] = commutator Position-momentum ${\displaystyle \sigma (x)\sigma (p)\geq {\frac {\hbar }{2}}\,\!}$ Energy-time ${\displaystyle \sigma (E)\sigma (t)\geq {\frac {\hbar }{2}}\,\!}$ Number-phase ${\displaystyle \sigma (n)\sigma (\phi )\geq {\frac {\hbar }{2}}\,\!}$ Dispersion of observable A = observables (eigenvalues of operator) ${\displaystyle {\begin{aligned}\sigma (A)^{2}&=\langle (A-\langle A\rangle )^{2}\rangle \\&=\langle A^{2}\rangle -\langle A\rangle ^{2}\end{aligned}}}$ General uncertainty relation A, B = observables (eigenvalues of operator) ${\displaystyle \sigma (A)\sigma (B)\geq {\frac {1}{2}}\langle i[{\hat {A}},{\hat {B}}]\rangle }$ Probability Distributions Property or effect Nomenclature Equation Density of states   ${\displaystyle N(E)=8{\sqrt {2}}\pi m^{3/2}E^{1/2}/h^{3}\,\!}$ Fermi–Dirac distribution (fermions) P(Ei) = probability of energy Ei g(Ei) = degeneracy of energy Ei (no of states with same energy) μ = chemical potential ${\displaystyle P(E_{i})=g(E_{i})/(e^{(E-\mu )/kT}+1)\,\!}$ Bose–Einstein distribution (bosons)   ${\displaystyle P(E_{i})=g(E_{i})/(e^{(E_{i}-\mu )/kT}-1)\,\!}$ Angular momentum[edit] Main articles: angular momentum operator and quantum number Property or effect Nomenclature Equation Angular momentum quantum numbers s = spin quantum number ms = spin magnetic quantum number ℓ = Azimuthal quantum number mℓ = azimuthal magnetic quantum number mj = total angular momentum magnetic quantum number j = total angular momentum quantum number Spin projection: ${\displaystyle m_{s}\in \{-s,-s+1\cdots s-1,s\}\,\!}$ Orbital: ${\displaystyle m_{\ell }\in \{-\ell ,-\ell +1\cdots \ell -1,\ell \}\,\!}$ ${\displaystyle m_{\ell }\in \{0\cdots n-1\}\,\!}$ Total: ${\displaystyle {\begin{aligned}&j=\ell +s\\&j\in \{|\ell -s|,|\ell -s|+1\cdots |\ell +s|-1,|\ell +s|\}\\\end{aligned}}\,\!}$ Angular momentum magnitudes angular momementa: S = Spin, L = orbital, J = total Spin magnitude: ${\displaystyle |\mathbf {S} |=\hbar {\sqrt {s(s+1)}}\,\!}$ Orbital magnitude: ${\displaystyle |\mathbf {L} |=\hbar {\sqrt {\ell (\ell +1)}}\,\!}$ Total magnitude: ${\displaystyle \mathbf {J} =\mathbf {L} +\mathbf {S} \,\!}$ ${\displaystyle |\mathbf {J} |=\hbar {\sqrt {j(j+1)}}\,\!}$ Angular momentum components   Spin: ${\displaystyle S_{z}=m_{s}\hbar \,\!}$ Orbital: ${\displaystyle L_{z}=m_{\ell }\hbar \,\!}$ Magnetic moments In what follows, B is an applied external magnetic field and the quantum numbers above are used. Property or effect Nomenclature Equation orbital magnetic dipole moment e = electron charge me = electron rest mass L = electron orbital angular momentum gℓ = orbital Landé g-factor μB = Bohr magneton ${\displaystyle {\boldsymbol {\mu }}_{\ell }=-e\mathbf {L} /2m_{e}=g_{\ell }{\frac {\mu _{B}}{\hbar }}\mathbf {L} \,\!}$ z-component: ${\displaystyle \mu _{\ell ,z}=-m_{\ell }\mu _{B}\,\!}$ spin magnetic dipole moment S = electron spin angular momentum gs = spin Landé g-factor ${\displaystyle {\boldsymbol {\mu }}_{s}=-e\mathbf {S} /m_{e}=g_{s}{\frac {\mu _{B}}{\hbar }}\mathbf {S} \,\!}$ z-component: ${\displaystyle \mu _{s,z}=-eS_{z}/m_{e}=g_{s}eS_{z}/2m_{e}\,\!}$ dipole moment potential U = potential energy of dipole in field ${\displaystyle U=-{\boldsymbol {\mu }}\cdot \mathbf {B} =-\mu _{z}B\,\!}$ The Hydrogen atom[edit] Main article: Hydrogen atom Property or effect Nomenclature Equation Energy level :p≈ En = energy eigenvalue n = principal quantum number e = electron charge me = electron rest mass ε0 = permittivity of free space h = Planck's constant ${\displaystyle E_{n}=-me^{4}/8\epsilon _{0}^{2}h^{2}n^{2}=-13.61eV/n^{2}\,\!}$ Spectrum λ = wavelength of emitted photon, during electronic transition from Ei to Ej ${\displaystyle {\frac {1}{\lambda }}=R\left({\frac {1}{n_{j}^{2}}}-{\frac {1}{n_{i}^{2}}}\right),\,n_{j}$

/