Αρχική Σελίδα > Τα μαθηματικά στις Φυσικές Επιστήμες. Διαφορικός Λογισμός. Μέρος πρώτο: Διαφορικές εξισώσεις και παραγώγιση σημαντικά εργαλεία για διατύπωση θεωριών στις Φυσικές Επιστήμες:

Τα μαθηματικά στις Φυσικές Επιστήμες. Διαφορικός Λογισμός. Μέρος πρώτο: Διαφορικές εξισώσεις και παραγώγιση σημαντικά εργαλεία για διατύπωση θεωριών στις Φυσικές Επιστήμες:

ΤΗΣ ΔΗΜΗΤΡΑΣ ΣΠΑΝΟΎ ΚΑΘΗΓΗΤΡΙΑΣ ΧΗΜΙΚΟΥ 1ου ΓΥΜΝ, ΔΑΦΝΗΣ

...Παίξαμε την ζωή μας μια ζαριά,

για να την μετουσιώσουμε σε κέρδος

Ο Λογισμός είναι ένας κλάδος των Μαθηματικών που επιτυγχάνει να έχει διαρκή αποτελέσματα κατά την διάρκεια των μεταβολών αυτών, είτε όσον αφορά τον τρόπο που γίνονται (κλίσεις καμπυλών στον διαφορικό λογισμό) ή τον υπολογισμό των συνολικών ποσοτήτων που παράγονται κατά την διάρκεια των μεταβολών αυτών με τον ολοκληρωτικό λογισμό

Στον Διαφορικό Λογισμό περιλαμβάνονται οι Σύνηθεις και οι Μερικές Διαφορικές Εξισώσεις

Ο ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ

Ο Διαφορικός Λογισμός ασχολείται με την μελέτη μεταβολών των ποσοτήτων και είναι μαζύ με τον Ολοκληρωτικό Λογισμό μια

από τις δυο παραδοσιακές διαιρέσεις του Λογισμού

$Διαφορικός λογισμός και Φυσική$

$Ο διαφορικός λογισμός στα μαθηματικά ασχολείται με τους ρυθμούς μεταβολής ποσοτήτων . Είναι άμεση η σχέση του με την Φυσική στην οποία συναντάμε διαρκώς μεγέθη που μεταβάλλονται (στην κίνηση το διάστημα μεταβάλλεται με τον χρόνο, στο ηλεκτρομαγνητικό πεδίο το ηλεκτρικό φορτίο με τον χρόνο, Το έργο δύναμης με το διάστημα μετατόπισης της δύναμης κ.α. Τα φαινόμενα αυτά μαθηματικοποιούνται και περιγράφονται πολλές φορές με κάποιες προσεγγίσεις , απλοποιήσεις και παραλλείψεις στοιχείων που ίσως έχουν μικρή ή αμεληταία επίδραση στο φυσικό φαινόμενο. Αυτά είναι τα μαθηματικά μοντέλα.$

$Οι Διαφορικές Εξισώσεις χρησιμοποιούνται για να περιγράψουμε προβλήματα Φυσικής, Γεωμετρίας, Ιατρικής, Βιολογίας, Τεχνολογίας, Χημείας.$

Υπάρχουν μεγέθη στις επιστήμες αυτές των η τιμή εξαρτάται από άλλα μεγέθη. μ= μ(λ).

Η παράγωγος dμ/dλ είναι συντελεστής μεταβολής που δίνει πόσο γρήγορα μεταβάλλεται το μέγεθος μ σε σχέση με το μέγεθος λ. Χρησιμοποιούμε τότε απλέςή σύνηθεις διαφορικές εξισώσεις

$Αν το μέγεθος μ εξαρτάται από δύο ή και περισσότερα μεγέθη μιλάμε τότε για μερικές παραγώγους$

Παράδειγμα σε κύκλωμα ηλεκτρικών ταλαντώσεων LC η ηλεκτρεγερτική δύναμη Ε εξαρτάται από την μεταβολή της τάσης στα άκρα του πυκνωτή

$Οι περιγραφές κάθε διαδικασίας στη Φύση, γίνονται μέσω μεταβλητών, που συνδέοντα ι με τον ρυθμό μεταβολής τους μέσω Φυσικών Νόμων .$

$Τα μαθηματικά αυτά μοντέλα, που οφείλουν την γένησή τους στην Μηχανική, την Αστρονομία και την θεωρητική Φυσική ήδη από την εποχή του Newton (1642-1727) και του Leibniz (1646-1716) αποτελούν συναρτήσιακές σχέσεις που περιέχουν μια άγνωστη συνάρτηση και ορισμένες παραγώγους της.$

$Στην συνέχεια αυτά τα μαθηματικά μοντέλα μελετώνται ως προς τις μαθηματικές ιδιότητές τους, ώστε να εξηγηθεί μαθηματικά η συμπεριφορά των φυσικών συστημάτων και να γίνουν πιθανές προβλέψεις για μελλοντική συμπεριφορά τους.$

$Κατά την επίλυση των διαφορικών εξισώσεων, συγκρίνεται η λύση με τις πειραματικές μετρήσεις και λέμε ότι το πρόβλημα έχει λυθεί μαθηματικά ή ότι η θεωρία έχει επαληθευτεί. Ακόμα πρέπει να ορίσουμε μέσα στο πεδίο ορισμού τιμές για την λύση της διαφορικής εξίσωσης . Στην Φυσική αυτό το λέμε αρχικές συνθήκες .$

$Αν οι τιμές δίνονται για περισσότερα από ένα σημεία λέγονται συνοριακές συνθήκες.$

$Θεωρείται ότι ο ι αρχικές συνθήκες μεταφέρουν πληροφορίες για τις τιμές του φυσικού μεγέθους κατά το παρελθόν ενώ οι συνοριακές συνθήκες για την επίδραση περιβαλλοντικών παραγόντων και την εξέλιξη του φαινομένου στο μέλλον$

$Σ ε ποιο πολύπλοκα συστήματα, δεν χρησιμοποιούμε μια μόνο διαφορική εξίσωση αλλά σύστημα διαφορικών εξισώσεων$

Η ιστορία των διαφορικών εξισώσεων στις Φυσικές Επιστήμες

Εισαγωγή των διαφορικών εξισώσεων στην Φυσική από τους Newton και Leibniz,

$Ο$ Newton επέτυχε να διατυπώσει το μαθηματικό μοντέλο και χρησιμοποίησε διαφορικές εξισώσεις στην απλή μορφή με σύνηθεις και μερικές παραγώγους

${\frac {dy}{dx}}=f(x)$ , ${\frac {dy}{dx}}=f(x,y)$ , $x_{1}{\frac {\partial y}{\partial x_{1}}}+x_{2}{\frac {\partial y}{\partial x_{2}}}=y$

ÎÏÎ¿ÏÎÎ»ÎµÏÎ¼Î± ÎµÎ¹ÎºÏÎ½Î±Ï Î³Î¹Î± Leibniz ενώ ο Leibniz το 1684 επέλυσε την εξίσωση του Νewton την μέθοδο των χωριζόμενων μεταβλητών ομογενών πρώτης τάξης η

dy/ dx = y/ a µέ λύση τήν ἐκθετική συνάρτηση

Ο L Leibniz επίσης εισήγαγε την έννοια της παραγώγου για την ποσότητα f ( x)΄ = dy/dx και του ολοκληρώματος ∫ f ( x dx ) .

Αντικείμενο μελέτης του είναι η παράγωγος συνάρτησης που είναι ο ρυθμός μεταβολής στο σημείο εισόδου. Η εύρεση της παραγώγου λέγεται παραγώγιση ή διαφόριση και γεωμετρικά αποτελεί την κλίση της εφαπτομένης στο σημείο που ζητάμε.

Παραδείγματα έχουμε στην κινηματική κατά την μελέτη της ταχύτητας και επιτάχυνσης

Κινηματική: Ταχύτητα και επιτάχυνση

$Δύο πολύ γνωστά μεγέθη της Φυσικής που αποτελούν παραγώγους είναι η ταχύτητα και η επιτάχυνση$

$Η ταχύτητα είναι η πρώτη παράγωγος της μετατόπισης προς τον χρόνο,$

$dy/dt =v(t) ή v(t)=y ΄$

$Η επιτάχυνση είναι η δεύτερη παράγωγος του διαστήματος προς τον χρόνο ή η πρώτη παράγωγος της ταχύτητας προς χρόνο$

$a(t)=d 2 y/dt 2 = y΄΄$

$και a(t)=d 2 v/dt 2$

Αν πρόκειται για διανυσματικά μεγέθη έχουμε τότε να κάνουμε παραγώγιση διανυσμάτων.

μετατόπιση είναι διανυσματικό μέγεθος, το ίδιο και η ταχύτητα. Άρα οι υπολογισμοί γίνονται στον διανυσματικό χώρο και υπολογίζουμε τόσο το μέτρο όσο και την κατεύθυνσή τους. ΔV=ΔX/Δt

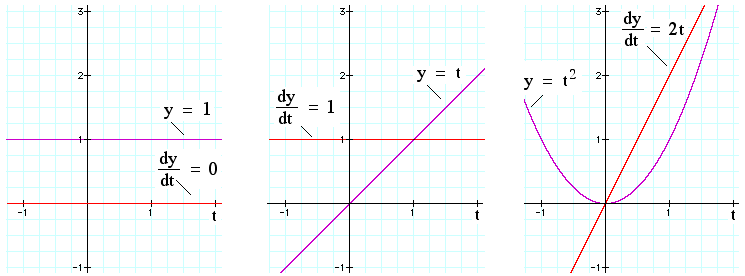$Έχουμε τις περιπτώσεις που η παράγωγος αυτή που εκφράζει ταχύτητα να είναι 0 (μετατόπιση μηδέν άρα σώμα ακίνητο)$

$Η παράγωγος να έχει μια σταθερή τιμή άρα έχω κίνηση ευθύγραμμη ομαλή και η μετατόπιση υπολογίζεται εύκολα από την σχέση που είναι ΔΕ$

$dy/dt=v --> dy =vdt$

$Το 1675 ὁ Leibniz γράφει ἐπί ϕύλλου χάρτου$ ∫ y dy = 1 /2 y ² από όπου μπορεί να υπολογιστεί το διάστημα που διανύει το κινητό με ολοκλήρωμα από το οποίο προκύπτει συνάρτηση 2ου βαθμού, οπότε,

Η κίνηση είναι ομαλά μεταβσλλόμενη και η μετατόπιση υπολογίζεται από συνάρτηση 2ου βαθμού.

Από αυτήν, η παράγωγος (ταχύτητα) είναι συνάρτηση πρώτου βαθμού της παραγώγου

είναι μια συνάρτηση του χρόνου 1ου βαθμού . v= (1/2y²)΄ =(1/2 v²t²)΄ =σταθερά.t =at

Παράδειγμα για την ομαλά μεταβαλλόμενη κίνηση a = Δv/ Δt

Υδροδυναμική , ροή ρευστών

Κατά τον 17ο και 18ο αιώνα γνωστοί μαθηματικοί όπως Jacob Bernoulli (1654-1705), Johann Bernoulli (1667-1748), Clairaut (1713- 1765), Riccati (1676-1754)

ασχολήθηκαν με την επίλυση διαφορικών εξισώσεων

Διαφορικές εξισώσεις 1ης τάξης και εξισώσεις Bernoulli και Riccati

H Διαφορική Εξισωση Bernoulli

d(y) /d(x) + P(x)y =Q(x)y^a

Διακρίνονται περιπτώσεις

1. Q(χ) =0 τότε d(y) /d(x) + P(x)y =0 [ομογενής γραμμική, 1ης τάξης)

2. Q(χ) όχι 0 η ΔΕ d(y) /d(x) + P(x)y =Q(x) λύνεται

Ο νόμος για την ροή είναι:

"Κατά μήκος μιας φλέβας ή ενός αγωγού που διέρχεται υγρό το άθροισμα της εξωτερικής πίεσης, της δυναμικής πίεσης και της υδροστατικής πίεσης είναι σταθερό".

Αργότερα οι Jacob Bernoulli (1654-1705), και ο Johann Bernoulli (1667-1748) Image result for Johann Bernoulli (1667-1748) ÎµÎ¾Î¹ÏÏÏÎµÎ¹Ï μελετoύν την ροή των ρευστών και την σχέση της ταχύτητας στην ροή με την πίεση και την διατομή του αγωγού ρ_ε

Η εξίσωση Bernoulli επιλύεται από τον Leibniz το 1696 και μετασχηματίζεται στην αντίστροφή της .

Image result for RICATTI DIFFERENTIAL EXTRACTION type

Eκτός από τον Bernouli o Riccati διατυπώνει μια εξ ίσου γνωστή διαφορική εξίσωση 2ου βαθμού

d(y) /d(x) = p(x)y ² +q(x)y +r(x)

οι p(x) , q(x) και r(x) είναι συνεχείς συναρτήσεις ορισμένες σε ένα διάστημα Ι που ανήκει στους παγματικούς αριθμούς.

Αν το r(x)=0 η εξίσωση Riccati ειναι η Bernoulli.

Λογισμός μεταβολών ή Αει ο Θεός ο Μέγας γεωμετρείν

Στις αρχές του 18ου αιώνα οι ΔΕ βοηθούν στην διατύπωση προβλημάτων Μηχανικής οι Euler (1701- 1783) και ο Γάλλος μαθηματικός Joseph-Louis Lagrange (1736-1813).

Μελετούν και και διατυπώνουν ΔΕ συι για κινήσεις που υπόκεινται σε δεσμούς ή περιγραφή συστημάτων που αποτελούνται από Ν σώματα

Στην επίλυση έχει εισαχθεί με ολοκληρωνων παράγοντας ή πολλαπλασιαστής Euler (1707-1783)

Ένα θεμελιώδες πρόβλημα του λογισμού των μεταβολών είναι να προσδιοριστούν σε ένα ορισμένο συναρτησιοειδές και ένα αντίστοιχο σύνολο μεταβολών που περιγράφονται από ένα άλλο σύνολο συναρτήσεων Α, που μεγιστοποιούνται και που ελαχιστοποιούνται οι συναρτήσεις αυτές

Δλαδή εισάγουν το θέμα των ακροτάτων των συναρτήσεων των μεταβολών

Στο τελευταίο τέταρτο του 19ου αιώνα, οι ΔΕ μελετώνται ως προς τρόπο επίλυσής τους. Peano (1858-1932) Αποδεικνύει την ύπαρξη λύσης ΔΕ

Lipschitz (1832-1903) Picard (1856-1941), Μελετούν τις λύσεις των ΔΕ ενώ

οι Poincare(1854-1912) Liapunor (1857-1918) Ασχολούνται με την ποιοτική συμπεριφορά των λύσεων όπως και τις τοπολογικές ιδιότητες των φάσεων και της συμπεριφοράς των λύσεων και γίνονται προόδοι στην ποιοτική θεωρία των ΔΕ.

Από ότι μπορούμε να δούμε φαίνεται πια η σχέση των μαθηματικών με τα Φυσικά μεγέθη και πόσο τα δεύτερα εκφράζονται από αυτά . Κάποιες προχωρημένες απόψεις θα πουν ότι μπορεί να γίνεται απλά το αντίστροφο άλλωστε ο

μνημονικός κανών αγνώστου συγγραφέως και εποχής, μας δίνει ταυτόχρονα τον ορισμό του π

Αεί ο Θεός ο Μέγας γεωμετρεί,
το κύκλου μήκος ίνα ορίση διαμέτρω,
παρήγαγεν αριθμόν απέραντον,
καί όν, φεύ,
ουδέποτε όλον θνητοί θα εύρωσι.

Κατά το πρώτο μισό του 20ου αιώνα, γίνονται σημαντικοί προόδοι στην ποιοτική θεωρία των ΔΕ από μαθηματικούς όπως ο Birkhoff (1884-1944) και ο Lofschetz (1884-1918)

Διαφορικές εξισώσεις συναντάμε όχι μόνο στην κλασσική θεωρητική φυσική αλλά σε όλες τις σχετικές επιστήμες (Χημεία, Βιολογία, Γεωλογία, Δημογραφία ...)

αλλά και ολές οι επιστήμες σήμερα χρησιμοποιούν τα μαθηματικά για ευκολότερη καταγραφή και αναλύσεις και προβλέψεις (Ιστορία, κοινωνιολογία

Ένα παράδειγμα εφαρμογών ΔΕ στην Χημεία είναι το πρόβλημα, του χημικού αντιδραστήρα

Μια ουσία εισέρχεται σε χημικό αντιδραστήρα με σταθερή ανάδευση με σταθερή παροχή q(v/t) και εξέρχεται με ρυθμό εξαγωγής ίσο με την παροχή q. Μέσα στον αντιδραστήρα η συγκέντρωση μιας ουσίας Α εξαρτάται από τον χρόνο c (t) και ο ρυθμός μεταβολής της εξαρτάται από την συγκέντρωσή της.

r (c) = m/V /t

Προσπαθούμε να διατυπώσουμε μια διαφορική εξίσωση για ισόθερμη μεταβολή ως εξής:

Η ταχύτητα μεταβολής μάζας της χημικής ουσίας Α είναι ίση με την ταχύτητα εισόδου q_c1 -(ταχύτητα εξόδου q_c+ ταχύτητα μεταβολής μάζας που καταναλώνεται στην αντίδραση). Δηλαδή

dV_c(t)/dt =q₁ -q_c(t) -v_r(c(t))

Αν υποθέσουμε ότι ο ρυθμός αντίδρασης r είναι ανάλογος της συγκέντρωσης r=kc τότε το πρόβλημα αχικών τιμών δίνεται από την διαφορική εξίσωση

( μαθηματικό μοντέλο):

dc/dt = q/V (c₁-c ) -kc₁

Ένα παράδειγμα εφαρμογών ΔΕ στην Βιολογία

Οι αμοιβάδες πολλαπλασιάζονται με "διχοτόμηση": κάθε αμοιβάδα, μετά παρέλευση, (κατά μέσο όρο), χρόνου τ από τη "γέννηση" της, διχοτομείται και δίνει δυο αμοιβάδες. Έστω ότι θέλουμε να μετρήσουμε τη μέση ζωή τ των αμοιβάδων. Για το σκοπό αυτό μετρούμε τον αριθμό Ν των αμοιβάδων σε μια καλλιέργεια τη στιγμή t=0 και τη στιγμή t=t₁ και βρίσκουμε Ν₀ και Ν₁ αντίστοιχα. Να υπολογιστεί το τ. (Υπόδειξη: Σε χρόνο τ ο αριθμός των αμοιβάδων διπλασιάζεται.)

Έστω έχουμε Ν ₀αμοιβάδες σε χρόνο t=0. Σε χρόνο t₁ o αριθμός των αμοιβάδων είναι Ν₁.

ΔΝ= Ν₁-Ν₀ ο αριθμός των διχοτομήσεων στην μονάδα του χρόνου είναι ανάλογος του αρχικού πλήθους Ν₀άρα: ΔΝ/Δt = λΝ₀

Από αυτό προκύπτει με μαθηματική λύση ότι o αριθμός των διχοτομήσεων είναι Ν(t) = ce^kt

Το c προκύπτει ως εξής: Σε t=0 έχουμε Ν(0) = ce^-λ0= c.1 =c δηλαδή Ν= Ν₀e^-λt

Σε χρόνο t₁ ; Ν₁= Ν₀e^-λt₁ (1)

Αν ζητάμε τον χρόνο υποδιπλασιασμού της αρχικής ποσότητας Ντ=Νο/2 έχουμε Νο/2 =Νοe^-λτ ->1/2 =e^-λτ ->

Παράδειγμα διαφορικής εξίσωσης στην οποία υπολογίζουμε τον ρυθμό διάσπασης ραδιενεργών πυρήνων

Απλό παράδειγμα σύνηθους διαφορικής εξίσωσης είναι ο ρυθμός διάσπασης ραδιενεργών πυρήνων που είναι ανάλογος των αδιάσπαστων πυρήνων:

dN/dt = -aN όπου Ν(t) οι αδιάσπαστοι ραδιενεργοί πυρήνες σε χρόνο t,

Απλό παράδειγμα σύνηθους διαφορικής εξίσωσης από την πυρηνική Φυσική

είναι ο ρυθμός διάσπασης ραδιενεργών πυρήνων που είναι ανάλογος των αδιάσπαστων πυρήνων:

dN/dt = -aN όπου Ν(t) οι αδιάσπαστοι ραδιενεργοί πυρήνες σε χρόνο t, No οι αδιάσπαστοι πυρήνες σε χρόνο t=0 και a σταθερά διάσπασης

στην επίλυση έχω dN/N =-adt ολοκληρώνουμε και έχουμε lnN = -at +c όπου lnNo = c και lnN = -at +lnNo --> lnN/lnNo =-at --> ln(N/No) =-at ---> N/No = e^-atd

Συνήθεις διαφορικές εξισώσεις είναι της δύναμης F= m.du/dt, (πρώτης τάξης και πρώτου βαθμού),

Ακόμα η εξίσωση (dy/dx)^3/2 +y³ = f(x) , είναι τρίτου βαθμού γιατί μπορεί να γραφεί (dy/dx)³ =[ -y³ + f(x) ]²

Κάποια είδη διαφορικών εξισώσεων

α.Σύνηθεις διαφορικές εξισώσεις: Περιέχει μια συνάρτηση μιας ανεξάρτητης μεταβλητής. Διακρίνονται σε ομοιογενείς και ανομοιογενείς, σε πρώτης και δευτέρας τάξης. y΄= f(x,y) Παραδείγματα:

dy/dx =2xy, xdy/dx =y-1, d²y/dx² =ax, d²y/dx² +dy/dx +y =0, du/dy = dy/dx, dx/dy + dx/dy +2 =0, d²u/dx² +d²u/dt² =2du/dt

Παραδείγματα σύνηθων διαφορικών εξίισώσεων

στην επίλυση έχω dN/N =-adt ολοκληρώνουμε και έχουμε lnN = -at +c όπου lnNo = c και lnN = -at +lnNo --> lnN/lnNo =-at --> ln(N/No) =-at ---> N/No = e^-atd

Συνήθεις διαφορικές εξισώσεις είναι της δύναμης F= m.du/dt, (πρώτης τάξης και πρώτου βαθμού),

Ακόμα η εξίσωση (dy/dx)^3/2 +y³ = f(x) , είναι τρίτου βαθμού γιατί μπορεί να γραφεί (dy/dx)³ =[ -y³ + f(x) ]²

β. Διαφορικές εξισώσεις με μερικούς παραγώγους:

Οι συναρτήσεις S, R, P είναι συναρτήσεις περισσότερων της μιας μεταβλητών.R΄ =R(x,y,z). Συνήθως γράφονται με κεφαλαίο γράμμα.

dS(t)/dt =-β[S(t)/P] I(t) +αR(t) + μ[ P -S(t)]

dR(t) = β[S(t)/P] I(t) -γI(t)

Μια τέτοια διάσημη εξίσωση μερικών παραγώντων είναι η εξίσωση Schrödinger

που είναι μερικών παραγόντων και δευτέρας τάξης.

Η m είναι η μάζα , Ε είναι η ολική ενέργεια και U η δυναμική ενέργεια. Η μορφή αυτή είναι χρονικά ανεξάρτητη (t=0) και για μια διάσταση.

Τα μικρά βελάκια στο σχήμα ονομάζονται διευθύνοντα στοιχεία από σημεία (x,y) με κλίση f(x). αν δεν παρέχουν αναλυτική λύση .η έναν τύπο για την f(x) , δίνουν όμως πληροφορίες για το σχήμα και την συμπεριφορά της λύσης.

$Σ ε ποιο πολύπλοκα συστήματα, δεν χρησιμοποιούμε μια μόνο διαφορική εξίσωση αλλά σύστημα διαφορικών εξισώσεων όπως στον αρμονικό ταλαντωτή με απόσβεση η εξίσωση είναι$

$md 2 y/dt +αdy/dx + ky =0 περιέχει τρεις αδιάστατες μεταβλητές, γιατί με επεξεργασία των t,y, m, a, k, l μπορούν να προκύψουν τρεις αδιάστατες μεταβλητές που επιλύονται με σύστημα διαφορικών εξισώσεων$

Δήμητρα Σπανού

ΠΗΓΕΣ

https://www.physics.upatras.gr/UploadedFiles/course_16_4956.pdf

https://mathbooksgr.files.wordpress.com/2011/12/diaforikes_sourlas_2007.pdf

https://www.physics.ntua.gr/~cchrist/SIMEIOSEIS/MATH.SYMPL.2003.PDF/KEFALAIO%2013%20.pdf

https://www.samos.aegean.gr/math/cnikolo/Science%20Modelling.pdf

https://www.physics.ntua.gr/mourmouras/metrhseis/aei_o_theos_o_megas.html

Riccati Equation

Math24

https://el.wikipedia.org/wiki/%CE%94%CE%B9%CE%B1%CF%86%CE%BF%CF%81%CE%B9%CE%BA%CE%AE_%CE%B5%CE%BE%CE%AF%CF%83%CF%89%CF%83%CE%B7Η Συμβολή της Επίλυσης του Προβλήματος του Βραχυστόχρονου στη ...

SlidePlayer.gr

20 Johann Bernoulli ..

Από το Νεύτωνα στον Weierstrass - ppt κατέβασμα

SlidePlayer.gr

23 Leonhard ...

https://repfiles.kallipos.gr/html_books/9863/Ch2.S2.html

https://myria.math.aegean.gr/epeaekI/courses/odigoi_askisewn/ODE/odek02/Lagrange/k02_lagrange.htm

https://www.math24.net/singular-solutions-differential-equations/

[PDF]ΔΥΝΑΜΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΓΡΑΜΜΕΣ

blogs.sch.gr

calculus - Very basic question about the definition of the derivative - Mathematics Stack Exchange

math.stackexchange.com

Σετ σταυρόνημα τρισδιάστατη υδρόγειο μεσημβρινό και παράλληλα, το ...

Depositphoto

ακατέργαστο

I = I (q 1, \dots, q n, q ˙ 1, \dots, q ˙ n, t)

I=I(q_{1},\ldots,q_{n},\dot{q}_{1},\ldots,\dot{q}_{n},t)

.που περιέχει n συναστήσεις Από τη συνθήκη

προκύπτουν οι εξής εξισώσεις Euler-Lagrange

Διαφορικές εξισώσεις στον Ηλεκτρισμό

Η ένταση του ηλεκτρικού ρεύματος

Το ηλεκτρικό ρεύμα μπορεί να διαρρέει έναν μονοδιάστατο αγωγό, μια επιφάνεια ή μια περιοχή του χώρου. Στην περίπτωση που ρέει έναν αγωγό χρησιμοποιείται κανονικά η ένταση του ηλεκτρικού ρεύματος για τη μέτρησή του.

Έτσι το μέγεθος που μετρά το ηλεκτρικό ρεύμα είναι η ένταση του ηλεκτρικού ρεύματος, που ορίζεται ως:

I={dQ \over dt}

Δηλαδή ένταση του ηλεκτρικού ρεύματος είναι ο ρυθμός διέλευσης του ηλεκτρικού φορτίου από τη διατομή ενός αγωγού. Μέγεθος μονόμετρο αλλά

Αν το ηλεκτρικό ρεύμα ρέει κατά μέτωπο μια επιφάνεια χρησιμοποιείται η επιφανεική πυκνότητα ηλεκτρικού ρεύματος που είναι

Electrical System Κύκλωμα L C Ηλεκτρικές ταλαντώσεις

Η Επαγωγική τάση που προκείται Εεπ = = -L.dI / dt.

Το ηλεκτρικό ρεύμα που διαρέει το κύκλωμα είνα I = dq / dt

Αντικαθιστώντας έχουμε Εεπ = - L. (d ) (dq / dt)/ dt

ακατεργαστο

\frac{d}{dt}\left(\frac{\partial L}{\partial\dot{q}_{k}}\right)-\frac{\partial L% }{\partial q_{k}}=0,\qquad k=1,\ldots,n.

x^{2}{\frac {d^{2}y}{dx^{2}}}+ax{\frac {dy}{dx}}+by=0.\,

Η πιο συνηθισμένη εξίσωση Cauchy-Euler είναι η εξίσωση δεύτερης τάξης, που εμφανίζεται σε μια σειρά εφαρμογών φυσικής και μηχανικής, όπως όταν λύνεται η εξίσωση Laplace σε πολικές συντεταγμένες. Η εξίσωση Cauchy-Euler δεύτερης τάξης

Άλλα φυσικά μεγέθη προκύπτουν από παραγωγήσεις

$Η Επιτάχυνση είναι η παράγωγος της ταχύτητας προς τον χρόνο$

Η Δύναμη επίσης είναι παράγωγος της ορμής. Εκφράζει τον ρυθμ΄μεταβολής της ορμής προς τον χρόνο

$Η Ένταση του ηλέκτρικού ρεύματος είναι ορυθμός μεταβολής του ηλεκτρικού φορτίου προς τον χρόνο$

$Η Ισχύς που είναι ο ρυθμός παραγωγής έργου ως προς τον χρόνο$

Στην Χημεία ο βαθμός αντίδρασης μιας χημικής αντίδρασης

Σημαντικό ρόλο στην Φυσική παίζουν οι διαφορικές εξισώσεις, όπως και τα μέγιστα και ελάχιστα αυτών που υπολογίζονται με την χρηση των παραγώγων.

ακατέργαστο

(1) Johann Bernoulli (1667-1748), Clairaut (1713-1765), Riccati (1676-1754)

{\displaystyle {\frac {dy}{dx}}=f(x)}

$Οι υπολογισμοί γίνονται βάσει των κανόνων$

$επίλυσης των διαφορικών εξισώσεων.$

$Στην περίπτωση αυτή η παράγωγος παίρνει διαφορετικές τιμές σε συνάρτηση με τον χρόνο και η συνολική μετατόπιση δεν μπορεί να υπολογισθεί απ ευθείας. Αυτό που γίνεται είναι να χωρήσουμε τον χρόνο σε μικρά Δt για τα οποία θα υποθέσουμε ότι η ταχύτητσ (η παράγωγος είναι σταθερή ) και θα υπολογίσουμε τις επι μέρους μετατοπίσεις και να τις αθροισουμε στην συνέχεια$

$Απο αυτήν την σκέψη θα προχωρήσουν τα Μαθηματικά στα οκοκληρώματα$

όμος τοΑν σε κλειστό βρόγχο μεταβληθεί με οποιονδήποτε τρόπο η μαγνητική ροή δημιουργείται τάση που είναι ανάλογη με τον ρυθμό μεταβολής της μαγνητικής ροής

slideplayer.gr

Αεί ο Θεός ο Μέγας γεωμετρεί, το κύκλου μήκος ίνα ορίση διαμέτρω, παρήγαγεν αριθμόν απέραντον, καί όν, φεύ, ουδέποτε όλον θνητοί θα εύρωσι.

Επαφή

Αεί ο Θεός ο Μέγας γεωμετρεί,
το κύκλου μήκος ίνα ορίση διαμέτρω,
παρήγαγεν αριθμόν απέραντον,
καί όν, φεύ,
ουδέποτε όλον θνητοί θα εύρωσι.