Δήμητρα Σπανού, χημικός, συνταξιούχος καθηγήτρια Μέσης Εκπαίδευσης από 30-6-2025
υπό κατασκευή
ΑΠΟ ΤΑ ΑΡΧΑΙΑ ΧΡΟΝΙΑ ΕΩΣ ΣΗΜΕΡΑ ΟΙ ΕΠΙΣΤΗΜΟΝΕΣ ΚΑΝΟΥΝ ΤΗΝ ΔΙΑΠΙΣΤΩΣΗ
ΟΤΙ Η ΦΥΣΗ ΤΕΙΝΕΙ ΠΡΟΟΔΕΥΤΙΚΑ, ΝΑ ΕΛΑΧΙΣΤΟΠΟΙΕΙ ΠΟΣΟΤΙΚΑ
ΤΟΝ ΤΡΟΠΟ ΔΙΕΞΑΓΩΓΗΣ ΟΛΩΝ ΤΩΝ ΕΚΔΗΛΩΣΕΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΦΑΙΝΟΜΕΝΩΝ
Από τον Αριστοτέλη που διατύπωσε την υπόθεση ότι "η φύση δεν κάνει τίποτα μάταια και σε όλες τις εκδηλώσεις επιλέγει τον συντομότερο ή ευκολότερο δρόμο", και τους μετέπειτα επιστήμονες που το κάνουν πιο συγκεκριμένο, όπως ο Κλαύδιος Πτολαιμαίος στην οπτική (Η ανακλωμενη ακτίνα ακολουθεί τον συντομότερο δρόμο) , και ο ο Pierre Fermat που το μελέτησε πολύ αργότερα 1662 μαζί με τον μαθηματικό Huygens ,και ο Λάιμπνιτς 1669, που πρώτος έθεσε τον όρο της έννοιας τη Δράσης σαν θεμελιώδη έννοια της Φυσικής. Ο μετά Νεύτωνα το 1687, που μελέτησε την ελαχιστοποίηση της αντίστασης στην κίνηση και άλλες αξιόλογες προσπάθειες.
Το μείζον (όπως πολύ αργότερα αποδείχθηκε) θέμα άρχισε αμυδρά να δίνει τις πραγματικές του διαστάσεις μετά από το έργο του Leonhard Euler για τον λογισμό των μεταβολών και οι υποψίες δικαιώθηκαν τον επόμενο αιώνα όταν ο william Rowan Hamilton δημοσίευσε την εργασία του πάνω στις εξισώσεις των μεταβολών, οι οποίες είχαν δεκαετίες διατυπωθεί πριν από δεκαετίες από τους Εuler- Lagrange. Ο Χάμιλτον με το έργο του έδωσε μια παραλλαγη- επέκταση των προηγούμενων εξισώσεων σε άλλα πεδία όπως το ηλεκτρομαγνητικό
Όταν στις αρχές τουν προηγούμενον αιώνα, μέσα από την κβαντική φυσική που στηρίζεται στην ερμηνεία των φαινομένων, σαν επαναλαμβανόμενες εμφανίσεις του ίδιου θέματος με διαφορετικές συντεταγμένες και με μαθηματική ακρίβεια (περιοδικότητα), υποψιάστηκαν πως η ελαχιστοποίηση ή και στασιμοποίηση της δράσης μπορεί να είναι η αρχή για μια ευρύτερη κατανόηση του φυσικού κόσμου πράγμα που άλλωστε έτεινε γενικότερα η ανθρώπινη διανόηση στις αρχές του 20ου αιώνα σε μια εναγώνια προσπάθεια και θαυμαστά αποτελέσματα
Η ΛΑΓΚΡΑΝΤΖΙΑΝΗ ΚΑΙ Η ΧΑΜΙΛΤΟΝΙΑ ΜΗΧΑΝΙΚΗ
Η Λαγκραντζιανή Μηχανική είναι μια διατύπωση της κλασσικής Μηχανικής όπως αναπτύχθηκε από τον Louis Lagrange το 1788.
Στην μηχανική Lagrangian η τροχαιά ενός αντικειμένου επιτυγχάνεται με την εύρεση της διαδρομής που ελαχιστοποιεί την δράση που είναι το ολοκλήρωμα της συνάρτησης Lagrange στον χρόνο. Η προσέγγιση Lagrange απλοποιεί πολλά προβλήματα της κλασσικής φυσικής (Νευτώνιας) γιατί τα επιλύει με την απλή αναζήτηση της πορείας της ελαχίστης δράσης.
Ένα μηχανικό σύστημα Lagrange χαρακτηρίζεται από γενικευμένες συντεταγμένες q (θέσεων) και τις πρώτες παραγώγους τους . ως προς τον χρόνο που αποτελούν τις ταχύτητες τους και ενδεχομένως ως προς τον χρόνο .
Το χρονικό ολοκλήρωμα από μια επιλεγμένη τροχαιά Lagrange είναι η δράση S
Η Χαμιλτονια Μηχανική είναι η διατύπωση της κλασσικής Μηχανικής όπως αναπτύχθηκε από τον William Hamilton το 1833 σε συνάφεια με την Λαγκραντζιαν. Σε αντίθεση με την προσέγγιση του Lagrange ο Ηαμιλτον χρησιμοποιεί την γενικευμένη ορμή αντί των ταχυτήτων που χρησιμοποιεί ο Lagrange γεγονός που την κάνει ιδιαίτερα χρήσιμη στην κβαντική και την στατιστική μηχανική
Ένα σύστημα Hamilton χαρακτηρίζεται από γενικευμένες συντεταγμένες q (θέσεων) και τις γενικευμένες παρορμήσεις τους p (ορμές) pi
Η συνάρτηση Hamilton περιγράφει την συνολική ενέργεια του συστήματος
ΟΙ ΓΕΝΙΚΕΥΜΕΝΕΣ ΣΥΝΤΕΤΑΓΜΕΝΕΣ
Οι γενικευμένες συντεταγμένες είναι ανεξέρτητοι παράμετροι οποιασδήποτε διάστασης, ο αριθμός των οποίων είναι ίσος με τους βαθμούς ελευθερίας του συστήματος που καθορίζουν τη θέση του συστήματος. Ο νόμος της κίνησης του συστήματος δίνει qi = qi(t) όπου t είναι ο χρόνος
Κατά την περιγραφή ενός σημείου όπως κι ενός διαχύσματος στην φυσική, πρέπει να γίνεται συγκεκριμένα και για τον λόγο αυτό ώστε καθορίζονται συστήματα συντεταγμένων.
Τα γνωστότερα συστήματα συντεταγμένων είναι τα εξής:

Α. Οι Καρτεσιανές Συντεταγμένες : ορίζουν την θέση ενός σημείου, στο επιπέδου (δισδιάστατο σύστημα. Δύο κάθετοι άξονες χ΄χ, ψ ψ΄) ή στον χώρο χρησιμοποιώντας τρεις κάθετους άξονες συντεταγμένων (τρισδιάστατο σύστημα. Τρείς κάθετοι άξονες χ΄χ, ψψ΄, ζ΄ζ) . Παράδειγμα η περιγραφή μία περιοχής στον χώρο (όγκος) που συχνά χρησιμοποιούμε για την κατανομή αριθμού μορίων στην στατιστική φυσική χρησιμοποιώντας τον όγκο που ορίζεται από το διάνυσμα της ταχύτητας
Κατά την περιγραφή ενός διανύσματος στον χώρο μπορεί το διάνυσμα αυτό σε γραφεί σε τρία διαμύσματα και να γραφεί σαν όπου τα ορθομοναδιαία διανύσματα
 Β. Το Κυλινδρικό Σύστημα Συντευαγμένων: Είνα ένα τρισδιάστατο σύστημα που προσδιορίζει την θέση ενός σημείου με τρεις παραμέτρους. Την ακτινική απόσταση ρ ή r από έναν άξονα αναφοράς (κυλινδρικός άξονας) , την γωνία φ ως προς μια επιλαγμένη διεύθυνση αναφοράς και την απόσταση z από ένα επιλεγμένο επίπεδο στον άξονα (υψος κυλίνδρου).
Β. Το Κυλινδρικό Σύστημα Συντευαγμένων: Είνα ένα τρισδιάστατο σύστημα που προσδιορίζει την θέση ενός σημείου με τρεις παραμέτρους. Την ακτινική απόσταση ρ ή r από έναν άξονα αναφοράς (κυλινδρικός άξονας) , την γωνία φ ως προς μια επιλαγμένη διεύθυνση αναφοράς και την απόσταση z από ένα επιλεγμένο επίπεδο στον άξονα (υψος κυλίνδρου).
Το σημείο αναφοράς του συστήματος είναι αυτό όπου όλες οι παράμετροι γίνονται μηδέν.
Το κυλινδρικό σύστημα έχει άπειρες ισοδύναμες συντεταγμένες (ρ, φ ± n×360°, z) και (−ρ, φ ± (2n + 1)×180°, z).
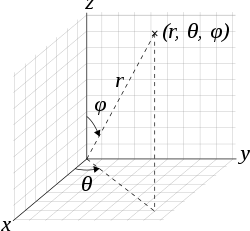 Γ. Το Σφαιρικό Σύστημα Συντεταγμένων : Αποτελεί μια γενίκευση του δισδιάστατου πολικού συστήματος συντεταγμένων. Η θέση ενός σημείου προσδιορίζεται από τρεις παραμέτρους: Την ακτινική απόσταση από ένα σταθερό σημείο αναφοράς (ακτίνα ή ακτινική συντεταγμένη) που είναι το κέντρο των αξόνων ο, την πολική γωνία που μετράται από σταθερή κατεύθυνση του ζενίθ που είναι ο άξονας z (για την φυσική, θ για τα μαθηματικά φ)και το αζιμούθιο η γωνία της προβολής του σημείου στο επίπεδο από κάποια σταθερή κατεύθυνση στο επίπεδο που είναι ο άξονας x. ( για την φυσική φ τα μαθηματικά θ)
Γ. Το Σφαιρικό Σύστημα Συντεταγμένων : Αποτελεί μια γενίκευση του δισδιάστατου πολικού συστήματος συντεταγμένων. Η θέση ενός σημείου προσδιορίζεται από τρεις παραμέτρους: Την ακτινική απόσταση από ένα σταθερό σημείο αναφοράς (ακτίνα ή ακτινική συντεταγμένη) που είναι το κέντρο των αξόνων ο, την πολική γωνία που μετράται από σταθερή κατεύθυνση του ζενίθ που είναι ο άξονας z (για την φυσική, θ για τα μαθηματικά φ)και το αζιμούθιο η γωνία της προβολής του σημείου στο επίπεδο από κάποια σταθερή κατεύθυνση στο επίπεδο που είναι ο άξονας x. ( για την φυσική φ τα μαθηματικά θ)
Η σχέση καρτεσιανών συντεταγμένων και σφαιρικών συντεταγμένων
Από σφαιρικές συντεταγμένες (r, θ, φ)περνάμε στις καρτεσιανές συντεταγμένες (x, y, z) ως εξής:
Από τις καρτεσιανές συντεταγμένες (x, y, z) )περνάμε στις σφαιρικές συντεταγμένες (r, θ, φ)ως εξής:
- 0, \\\\\n\\sgn(y)\\frac \\pi 2 & ,\\gamma\\iota\\alpha\\; x = 0, \\\\\n\\arctan(\\frac y x) + \\pi & ,\\gamma\\iota\\alpha\\; x < 0 \\land y \\geq 0, \\\\\n\\arctan(\\frac y x) - \\pi & ,\\gamma\\iota\\alpha\\; x < 0 \\land y < 0. \\end{cases}"}}" id="mwXg" style="font-size:14px;" typeof="mw:Extension/math">
- ΟΙ ΓΕΝΙΚΕΥΜΕΝΕΣ ΠΑΡΟΡΜΗΣΕΙΣ
- Στην Χαμιλτόνια η Λαγκρατζιανή συνάρτηση οι όροι εκφράζονται με τιμές γενικευμένων συντεταγμένων και γενικευμένων ταχυτήτων και η διάσταση της συντεταγμένης εξαρτάται από τη διάσταση της γενικευμένης συντεταγμένης.
- Αν η συντεταγμένηqi έχει τη διάσταση του μήκους τότε η παρόρμηση pi έχει την διάσταση της ορμής που είναι η μάζα επί την ταχύτητα.
- Αν η συντεταγμένη qi είναι γωνία (αδιάστατη ποσότητα) τότε το i έχει τη διάσταση της γωνιακής ορμής
.jpg)
Δήμητρα Σπανού
ΠΗΓΕΣ
Χαμιλτονιανή Μηχανική | Θεωρητική Φυσική. Σχολικό βιβλίο
Λαγκρανζιανή μηχανική - Βικιπαίδεια
https://el.wikipedia.org/wiki/%CE%9A%CE%B1%CF%81%CF%84%CE%B5%CF%83%CE%B9%CE%B1%CE%BD%CF%8C_%CF%83%CF%8D%CF%83%CF%84%CE%B7%CE%BC%CE%B1_%CF%83%CF%85%CE%BD%CF%84%CE%B5%CF%84%CE%B1%CE%B3%CE%BC%CE%AD%CE%BD%CF%89%CE%BD
https://el.wikipedia.org/wiki/%CE%9A%CF%85%CE%BB%CE%B9%CE%BD%CE%B4%CF%81%CE%B9%CE%BA%CE%AD%CF%82_%CF%83%CF%85%CE%BD%CF%84%CE%B5%CF%84%CE%B1%CE%B3%CE%BC%CE%AD%CE%BD%CE%B5%CF%82
https://el.wikipedia.org/wiki/%CE%A3%CF%86%CE%B1%CE%B9%CF%81%CE%B9%CE%BA%CF%8C_%CF%83%CF%8D%CF%83%CF%84%CE%B7%CE%BC%CE%B1_%CF%83%CF%85%CE%BD%CF%84%CE%B5%CF%84%CE%B1%CE%B3%CE%BC%CE%AD%CE%BD%CF%89%CE%BD
Γενικευμένες παρορμήσεις, ενέργεια
Ταλαντώσεις με αρκετούς βαθμούς ελευθερίας
Φυσική Εγκυκλοπαίδεια




 .
.

 όπου
όπου 





