ΧΗΜΕΙΑ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Κεφ6 Ηλεκτρονιακή Δομή των Ατόμων έως Περιοδικος Πίνακας

Τι θα πρέπει να καταλάβουμε από το βιβλίο της Χημείας Προσανατολισμού Γ τάξης Ενιαίου Λυκείου. Μια προσπάθεια να τονίστουν τα βασικά σημεία του μαθήματος με στόχο την κατανόησή του

από την Δήμητρα Σπανού χημικό, καθηγήτρια Δευτεροβάθμιας Εκ/σης 1ου Γυμνασίου Δάφνης

 

Παρ ότι είμαι καθηγήτρια Χημικός έχω πολλά χρόνια να διδάξω την Χημεία της Θετικής Κατεύθυνσης 

 στην οποία από ότι  ξέρω , έχουν γίνει  κάποιες αλλαγές στην ύλη από παλιά, που την δίδασκα φροντιστηριακά.

Θα ξεκινήσω μια   προσπάθεια ,να δώσω με απλό και  όσο γίνεται σύντομο  τρόπο ,την ύλη του βιβλίου αυτού ,

 με στόχο να μπορεί ο υποψήφιος  να έχει , αρχικά, μια  εικόνα σχετικά για  τα θέματα που θα τον απασχολούν ανά κεφάλαιο

Ταυτόχρονα είναι και για μένα μια καλή ευκαιρία θα τα ξαναθυμηθώ και να ενημερωθώ για την ύλη της φετινής σχολικής χρονιάς

Δήμητρα Σπανού

 

ΑΠΟ ΤΗΝ ΕΞΕΤΑΣΤΕΑ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΛΥΚΕΙΩΝ 2016-2017 ΧΗΜΕΙΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ

Πρώτο Μέρος

Κεφάλαιο «ΗΛΕΚΤΡΟΝΙΑΚΗ ΔΟΜΗ ΤΩΝ ΑΤΟΜΩΝ ΚΑΙ ΠΕΡΙΟΔΙΚΟΣ ΠΙΝΑΚΑΣ»

ΕKTΟΣ ΑΠΟ: υποενότητα «Ηλεκτροσυγγένεια» της παρ. «Μεταβολή ορισμένων περιοδικών ιδιοτήτων» και αρ. «Ηλεκτρονιακοί τύποι - Σχήματα μορίων»

Εισαγωγή

Στόχος της Χημείας αλλά όλων των επιστημών είναι να εντάσσει τις νέες γνώσεις, προόδους και εξελίξεις, στα ήδη κατεκτημένα της, επίσης να εξετάζει σημεία που τυχόν χρειάζονται ακόμη περισσότερη διασαφήνιση,  αλλά και άλλα που  θα πρέπει να καταρριφθούν . 

Στην επιστήμη της Χημείας, η οποία όσο εμβαθύνει και εξελίσσεται  βρίσκεται σε συγγενικές περιοχές με τις άλλες φυσικες επιστήμες,  το κεφάλαιο αυτό o Bohr

συνδέει την επαναστατική για την εποχή της θεωρία του Rutheford  με τις νέα σαρωτικά ανοίγματα  της κβαντικής θεωρίας και όπως εφαρμώσθηκαν στην Κβαντική Χημεία. Αυτό θα μας οδηγήσει στην συνέχεια , να έχουμε μια άλλη πιο βαθιά και καθαρή εικόνα γι α τον περιοδικό πίνακα, στον οποίο βέβαια ήδη από την αρχή που διατυπώθηκε   υπήρχαν μέσα σε αυτόν σημεία που δεν είχαν ερμηνευτείτ

Στο σχήμα των τροχαιών ο Bohr

δεν προχώρησε παραπέρα και προτείνε το ίδιο δηλαδή σφαιρικό, σχήμα που ίσχυε από τον προηγούμενο φυσικό τον  Rutherford 

πράγμα που δεν είναι αλήθεια ειδικότερα για μεγαλύτερα άτομα. Αλλά και μέχρις εδώ ο Bohr έδσε μια μεγάλη ώθηση στην μελέτη της  Χημεία της κατασκευής του ατόμου

 

(sel 2-4)Τροχιακό και κβαντικοί αριθμοί

Ο Neils Bohr Δανός φυσικός (1885-1962) έκανε ακριβώς αυτό.  Πάνω στο πρότυπο του ατόμου του Rutherford που περιγράφει το γνωστό μας άτομο με τον πυρήνα στο κέντρο και τα αρνητικά ηλεκτρόνια να περιστρέφονται σε τροχαιές, εφάρμοσε τις αρχές της κβαντικής θεωρίας κατά την οποία τα φυσικά μεγέθη είναι κβαντισμένα.  Αυτό σημαίνει  οι τιμές που παίρνουν δεν είναι τυχαίες αλλά  πάντα πολλαπλάσια μιας στοιχειώδους μονάδας .

 Οι δυο συνθήκες του  Bohr

Στην πρώτη συνθήκη ο Bohr εφαρμόζει την κβαντική θεωρία για

.  1. Την ενέργεια που έχουν τα περιστρεφόμενα στις στοιβάδες ηλεκτρόνια, (και κατά συνέπεια  αναφέρεται και στο μήκος της  ακτίνας της τροχαιάς τους,  εφ όσον η ενέργεια σχετίζεται με αυτήν ) 

Και στην δεύτερη συνθήκη ο   Bohr εφαρμόζει την κβαντική θεωρία για 

2. Την ενέργεια που εκπέμπουν ή απορροφούν  αφού διασαφηνίστηκε ότι η εκπομπή ή απορράφηση ενέργειας από τα ηλεκτρόνια, συμβαίνει μόνο όταν αυτά αλλάζουν στοιβάδα σύμφωνα με την ενέργεια που έχουν κάθε φορά .

Βέβαια ο Bohr 

 

Αναλυτικότερα 

Στη πρώτη συνθήκη του Bohr η ενέργεια του ηλεκτρονίου υπολογίστηκε ίση με όπου n=1,2,3,4,... είναι ο κύριος κβαντικός αριθμός  που καθορίζει την ενεργειακή στάθμη , (αλλά και την απόσταση από τον πυρήνα) .Το αρνητικό πρόσημο σημαίνει ότι για να φτάσει το ηλεκτρόνικο στο σημείο μηδενικής ενέργειας (μέγιστη τιμή) , και έτσι να ξεφύγει από την έλξη πρέπει να πάρει ενέργεια που λέγεται ενέργεια ιοντισμού. Η ενέργεια αυξάνεται (μειώνεται η αρνητική τιμή) και πλησιάζει προς το μηδέν όταν μεγαλώνει ο κύριος κβαντικός αριθμός n , δηλαδή απομακρύνεται από τον πυρήνα και την έλξη του.

Η σταθερότερη κατάσταση είναι αυτή με την μικρότερη ενέργεια δηλαδή εδώ με την μεγαλύτερη αρνητική τιμή. Αυτό προυποθέτει το n να πάρει την μικρότερη δυνατή τιμή  δηλαδή τα ηλεκτρόνια νε είναι όσο γίνεται πιο κοντά στον πυρήνα. Αυτή η κατάσταση λέγεται θεμελιώδης.

Στην δεύτερη συνθήκη του Bohr φαίνεται που πάει η διαφορά της ενέργειας μεταξύ των διάφορων κβαντικών  ενεργειακών καταστάσεων  όπως προκύπτουν από την πρώτη συνθήκη και καθώς αλλάζει το n. (τις λέμε κβαντικές γιατί υπάρχει το n που τις κάνει να παίρνουν συγκεκριμένες τιμές)

Η διαφορά αυτή στην ενέργεια τν στοιβάδων ανταλλάσσεται με το περιβάλλον δηλαδή 

εκπέμπεται εάν είναι θετική απο έξω στοιβάδα (μεγαλύτερο το  n μικρότερη αρνητική ενέργεια το κλάσμα άρα μεγαλύτερη) σε μέσα (μικρότερη ενέργεια)

απορροφάται  εάν η μεταβολή  στην ενέργεια αρνητική  απο μέσα  στοιβάδα (μικρότερο το  n μικρότερη αρνητική ενέργεια το κλάσμα άρα μεγαλύτερη) σε μέσα (μικρότερη ενέργεια)

Και εφόσον οι ενέργειες στις στοιβάδες είναι κβαντισμένες (συγκεκριμένες τιμές) θα  είναι  κβαντισμένη και  η διαφορά τους.

Η ενέργεια ηλεκτρονίων που μεταπίπτουν σε στοιβάδες  εκπέμπεται σαν ηλεκτρομαγνητική  ακτινοβολία,   σε μικρά πακέτα (κβάντα) ενέργειας και 

η συχνότητά της είναι ανάλογη με την ενέργειά της . Ε=hν  Έτσι έχουμε εκπομπή στην υπέρυθρο, την ορατή την γ κ.λ.π. περιοχές ανάλογα με την ενέργεια που ελευθερώνεται από την μεταπήδηση στις στοιβάδες. 

Πάντα όμως  ισχύει  Ε (που εκπέμπεται) = ΙΕ₂ -Ε₁Ι =hv

Το h είναι μια σταθερά h η σταθερά του Plank. H θεωρία του Bohr εξηγεί το γραμμικό φάσμα της εκπομπής που δίνει  το υδρογόνο. Οι γραμμές δείχνουν πως η ενέργεια που εκπέμπεται δεν είναι συνεχής αλλά κβαντισμένη.

Δεν καταφέρνει να ερμηνεύσει φάσματα πιο πολύπλοκών ατομων

 

Σύγχρονες θεωρίες για τα άτομα

(sel6)1. Κυματική θεωρία της ύλης του De Broglie

Προσπάθησε να ερμηνεύσει την διττή φύση του φωτός που άλλωτε εμφανίζει συμπεριφορά ηλεκτρομαγνητικού κύματος (λ.χ. δίνει φαινόμενα περίθλασης και συμβολής όπως όλα τα κύματα) και άλλωτε σαν σωματίδιο (ανακλάται σε λείες επιφάνειες)

Το κβάντο του φωτός σε ορισμένη συχνότητα ονομάζεται φωτόνιο 

Διατυπώνει έμμεσα την ιδέα ότι τα κινούμενα σώματα πάντα εμφανίζουν διττή φύση. Σώματος και κύματος. Το μήκος κύματος είναι ίσο με 

Από αυτήν την σχέση φαίνεται πως αν έχουμε ένα σώμα με μια  μάζα δικών μας διαστάσεων  όπως ένα μπαλάκι του τένις που κινείται με μια ταχύτητα 65km/h αυτο σύμφωνα με τον de Broglie ταυτόχρονα μπορεί να θεωρηθεί και σαν υλικό κύμα όπου λ <10^-33. Αυτό είναι πολύ μικρό για τις διαστάσεις του πολύ μικρότερο  ακόμα και από τους πυρήνες των ατόμων που αποτελούν το σώμα και έτσι δεν γίνεται αντιληπτό σαν κύμα.

Εάν όμως έχουμε ένα πολύ μικρό σωματίδιο όπως το ηλεκτρόνιο, που κινείται με πολύ μεγάλη ταχύτητα το μήκος κύματος μεγαλώνει πολύ και φτάνει περίπου στα 10^-10m που μπορεί  να ανιχνευτεί σαν  υλικό κύμα .

Αρχή της Αβεβαιότητας του Heisenberg

Η αρχή αυτή λέει πως 

Είναι δύσκολο να προσδιορίσουμε με ακρίβεια συγχρόνως την θέση και την ορμή ενός σωματιδίου

Η μεγάλη ακρίβεια στον προσδιορισμό της θέσης ενός ηλεκτρονίου συνεπάγει μεγάλη  αβεβαιότητα κατά τον προσδιορισμό της ορμής του. Αυτό ισχύει κυρίως για σωματίδια με πολύ μικρές μάζες και μεγάλες ταχύτητες όπως τα υποατομικά. Η παραδοχή της αρχής της αβεβαιότητας καταρρίπτει μονέλα όπως το πλανητικό μοντέλο του Rutherford εφ όσον δεν μπορεί να είναι γνωστά  ταυτόχρονα, η θέση και η ταχύτητα του ηλεκτρονίου σε κυκλική τροχαιά. Οδηγεί αργότερα σε  άλλες προοπτικές όπως είναι τα ατομικά τροχιακά

 απο την Βικιπαίδεια (https://el.wikipedia.org/wiki/Αρχή_της_απροσδιοριστίας)

Η βασική έκφραση της αρχής της απροσδιοριστίας είναι αυτή του 1927:

Εάν μετράμε τη θέση ενός σωματίου με αβεβαιότητα Δx και ταυτόχρονα μετράμε την ορμή του με αβεβαιότητα Δp, τότε το γινόμενο των δύο μεγεθών δεν μπορεί να είναι μικρότερο από έναν αριθμό της τάξης του {\displaystyle \hbar } (όπου {\displaystyle \hbar =h/2\pi }). Δηλαδή:

${\displaystyle \Delta x\cdot \Delta p\geq {\frac {\hbar }{2}}}$

 

(sel7) Η εξίσωση του Strondinger

Μας δίνει την δυνατότητα να συνδέσουμε και να παρουσιάσουμε με μια μαθηματική σχέση την περιγραφή ενός σωματιδίου και ταυτόχρονα την κυματοειδή συμπεριφορά του. Στην σχέση συμπεριλαμβάνονται η μάζα, το ηλεκτρικό φορτίο, οι   επιδράσεις της μηχανικής ενέργειας

Για να το πετύχει εγκαταλείπει την ιδέα του προσδιορισμού της θέσης του σωματιδίου όπως παραδοσιακά την εννοούμε και εισάγει την ιδέα της πιθανότητας να βρεθεί το σωματίδιο σε ορισμένο  χώρο. Η εξίσωση θεωρείται αριστουργηματική γιατί, από ότι έχει ειπωθει, μπορεί να περιγράψει τα πάντα, περιγράφει την φύση. Έχει τεράστιο αριθμό από εφαρμογές όπου εισάγοντας τις ειδικές παραμέτρους για κάθε σωματίδιο που θέλουμε να μελετήσουμε, καταλήγουμε σε εξισώσεις που το περιγραφου. Συγκεκριμένο παράδειγμα  εάν εισάγουμε την ορισμένη ενέργεια ενός ηλεκτρονίου στην εξίσωση Strondinger αυτή οδηγεί σε κυματοσυναρτήσεις ψ που ονομάζονται ατομικά τροχιακά είναι ορισμένες για την συγκεκριμένη τιμή της ενέργειας (εννοείται πως  διαφέρουν στις στοιβάδες ) και είναι της μορφής ψ(x,ψ,z) 

Η κυματοσυνάρτηση Ψ είναι μιγαδική και δεν είναι εύκολο να προσδιοριστεί με ακρίβεια η φυσική της σημασία εκτός από το ότι, αποτελεί ένδειξη της παρουσίας ή όχι ηλεκτρονίου γυρω από τον πυρήνα. ψ=0 αποσία ψ οχι 0 παρουσία. 

Όμως η ψ² (παύει να είναι μιγαδική)έχει σημαντική φυσική σημασία και εκφράζει  την πιθανότητα να βρεθεί ένα ηλεκτρόνιο σε ορισμένο σημείο του χώρου γύρω από τον πυρήνα

Το -e ψ²  εκφράζει την κατανομή ή την πυκνότητα του ηλεκτρονιακού νέφους στο χώρο γύρο από τον πυρήνα. (e το φορτίο του ηλεκτρονίου)

Η εξίσωση περιγράφει καλά το άτομου του υδρογόνου . Μπορεί όμως να εφαρμοστεί και σε πολυπλοκότερα άτομα η επίλυσή της όμως αποτελεί ένα πολύπλοκο μαθηματικό πρόβλημα. 

Η σχηματική απεικόνιση του ηλεκτρονιακού νέφους (της ψ² ) του ατόμου του υδρογόνου στην θεμελιώδη κατάσταση 

(οχι το τροχιακό όπως αναφέρεται καμμιά φορά)

το ηλεκτρονιακό νέφος έχει μεγίστη πυκνότητα κοντά στον πυρήνα

(sel9) Κβαντικοί αριθμοί

Η κβαντομηχανική είναι η θεμελιωμένη πλέον θεωρία της Φυσικής που εμηνεύει φαινόμενα, τα οποία η μέχρι τότε Νευτώνεια Φυσική αδυνατούσε να ερμηνεύσει. Περιγράφει την συμπεριφορά της ύλης σε ατομικό, μοριακό και υποατομικό επίπεδο. Η βασική της αρχή είναι ότι οι φυσικές ποσότητες όπως η ενέργεια η μάζα, το ηλεκτρικό φορτίο και άλλες, απαρτίζονται η κάθε μια από βασικές ποσότητες διακριτές που αποτελούν τα κβάντα 

Η εξίσωση Strondinger όπως είπαμε περιγράφει την κατάσταση σωματιδίων και συμπεριλαμβάνει τις παραμέτρους που καθορίζουν την συμπεριφορά τους που είναι η μάζα, το φορτίο τυχόν επιδράσεις δυναμικών πεδίων κ.λ.π.

Εάν θεωρήσουμε την εξίσωση αυτή για το άτομο του υδρογόνου και την επιλύσουμε προκύπτουν 3 λύσεις.  Οι λύσεις αυτές θα δώσουν τις κβαντικές τιμές για φυσικά μεγέθη που συνδέονται με την συμπεριφορά του ατόμου του υδρογόνου όπως και είναι για μεγαλύτερα άτομα.

Α. το  μέγεθος τροχιακού ( n)  (που σχετίζεται με την απόσταση από τον πυρήνα και συνεπώς με την ενέργεια) 

Β.  Τοσχήμα τροχιακού (l) (που σχετίζεται με τις υποστοιβάδες σε μια στοιβάδα ηλεκτρονίων )

Γ.τον προσανατολισμό του τροχιακού (m_l)   (που δίνει τον προσανατολισμό του νέφους (κατανομή) στους άξονες x,ψ,z  )

 και αποκαλούνται κβαντικοί αριθμοί

Αναλυτικά

Η πρώτη λύση είναι ο κύριος κβαντικός αριθμός n που παίρνει τιμές ακέραιες (1, 2, 3, 4, ...) 

(Τον έχουμε συναντήσει στην πρώτη συνθήκη του Bohr, να καθορίζει εκεί τις επιτρεπτές τιμές της Ενέργειας του ηλεκτρονίου, η οποία βέβαια σχετίζεται με την απόσταση του ηλεκτρονίου από τον πυρήνα. (νόμος του coulomb) δηλαδή την τροχαιά του).

Εδώ το ίδιο πράγμα εκφράζεται διαφορετικά

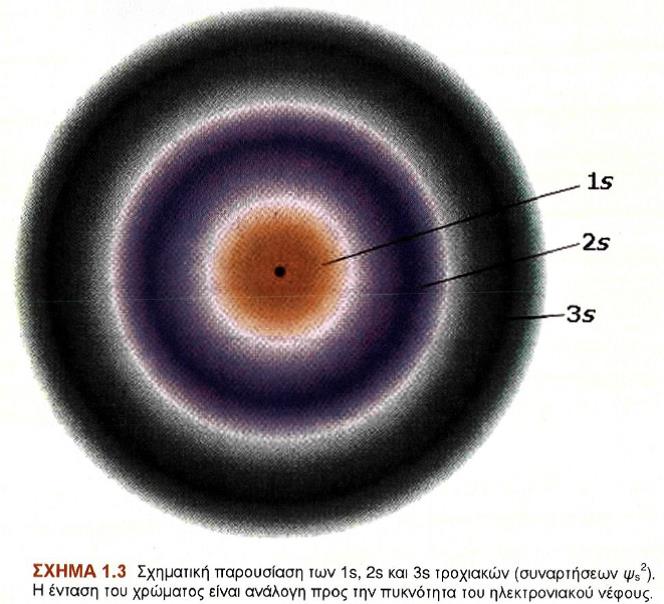Ο κύριος κβαντικός αριθμός n καθορίζει το μέγεθος του ηλεκτρονιακού νέφους ή τροχιακό. 

Όσο μεγαλύτερες τιμές παίρνει το n τόσο μεγαλύτερο χώρο καταλαμβάνει η περιοχή που επιρρεάζεται από το ηλεκτρόνιο (η κατανομή πιθανότητας να βρίσκεται εκεί ή μέγεθος ηλεκτρονιακού νέφους). Αυτό  βέβαια,  έχει κάποιο σημείο που  εμφανίζει μέγιστο στην κατανoμή της πιθανότητας και αυτά μπορούν να παραλληλιστούν με τις τροχαιές του Bohr (σκουρότεροι τόνοι στην πορτοκαλί, την μπλε κσι την μολυβί περιοχή στο διπλανό σχήμα στις οποίες έχουμε αντίστοιχα n=1,  n=2,  n=3,

Η δεύτερη  λύση είναι ο δευτερεύων κβαντικός αριθμός ή αζιμουθιακός l  που παίρνει τιμές ανάλογα με τον n  μειωμένο κατα 1: (0, 1, 2, 3, ...( n-1))

και καθορίζει το σχήμα του ηλεκτρονιακού νέφουςι . 

Για n=1 το l έχει μια τιμή l =0 και έχουμε μια υποστοιβάδα με σφαιρική συμμετρία την υποστοιβάδα s

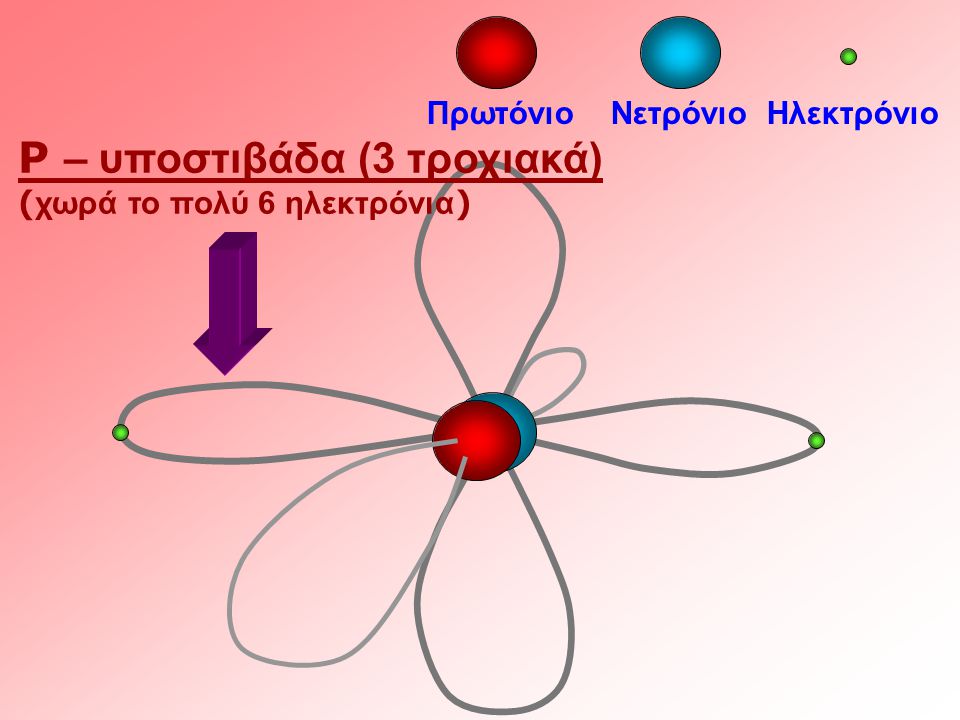Για n=2 το l έχει 2 τιμές l =0 l =1 και έχουμε 2 υποστοιβάδες την s και την p. Για  l =1η συμμετρία της υποστοιβάδας είναι διπλού λοβού και η υποστοιβάδα είναι η p

Ο μαγνητικός αριθμός ml  καθορίζει τον προσανατολισμό του ηλεκτρονιακού νέφους όπως  διαμορφώνεται  με την  κατανομή της πιθανότητας  στους 3 άξονες χ.ψ.ζ.)  στο σχήμα έχουμε 3 υποστοιβάδες p κατανεμημένες στους 3 άξονες. οι τιμές του εξαρτώνται από το l και  παίρνει τις τιμές l-,  -(l+1) ,  ...0,  1,  ...(l  +1) , l  

Ο κβαντικός αριθμός του spin m_s είναι ανεξάρτητος των άλλων και παίρνει τιμές +1/2 και -1/2 

Γραφική απεικόνιση των ατομικών 

(sel 11) Γραφική απεικόνιση ατομικών τροχιακών

Η γραφική απεικόνιση των ατομικών τροχιακών ή αλλιώς της πυκνότητας του ηλεκτρονιακού νέφους

  (ας μην φανταστούμε ένα πλήθος ηλεκτρονίων να γεμίζουν τον χώρο γύρω από τον πυρήνα αλλά την "ηλεκτραρνητικότητα" που αντιστοιχεί στα διάφορα σημεία του και που κυρίως σχετίζεται με τον χρόνο που παραμένει το κινούμενο ηλεκτρόνιο στα σημεία αυτά)

μπορεί να δοθεί με πολλούς τρόπους αλλά ο πιο συνηθισμένος είναι με την παράσταση των συναστήσεων ψ²

Βέβαια ενώ εδώ αναπαριστάνουμε κατανομή στον χώρο,  στο διάγραμμα που θα πάρουμε, θα αρκεστούμε στο περίγραμμα της καμπύλης που όμως δίνει το 90-99% της πυκνότητας του ηλεκτρονιακού νέφους που είναι ικανοποιητικό για να έχουμε την εικόνα τους

Τοποθετώντας τις τετράδες τους κβαντικούς αριθμούς έχουμε την εικόνα όχι μόνο του ατόμου του υδρογόνου, αλλά και μεγαλύτερων ατόμων ώσπου θα δούμε στο τέλος καθαρή την λογική της τοποθέτησης των στοιχέιων στον περιοδικό πίνακα

 

Περιπτώσεις   

 για την πρώτη στοιβάδα n=1  το l=0 έχουμε σφαιρική συμμετρία και 1 υποστοιβάδα την1s 

για την δεύτερη στοιβάδα το  n=2  και  το l παίρνει 2 τιμές :το l=0  και ml =0 που σημαίνει πως έχουμε ένα σφαιρικό τροχιακό στην2s υποστοιβάδα   και  l=1  ενώ το ml παίρνει τις τιμές -1, 0, και 1 πράγμα που σημαίνει πως έχουμε 3 λοβούς 

 

 

 

(sel 13) Αρχές δόμησης πολυηλεκτρονιακών ατόμων

Στο ηλεκτρόνιο στην θεμελιώδη κατάσταση με την χαμηλώτερη ενέργεια το μοναδικό  ηλεκτρόνιο τοποθετείται στο τροχιακό 1s. ΣΕ διεγερμένη κατάσταση με πρόσληψη ενέργειας μπορεί να βρεθεί σε ανώτερα τροχιακά (διεγερμένη κατάσταση)

Σε πολυηλεκτρονιακά άτομα η λεγόμενη ηλεκτρονιακή δόμηση, δηλαδή η συμπλήρωση των τροχιακών με ηλεκτρόνια, ακολουθεί ορισμένες αρχές.  Έχει δε μεγάλη σημασία γιατί μέσω αυτής διαμορφώνεται η ηλεκτρονιακή δόμηση του ατόμου αλλά και η χημική του συμπεριφορά.

Απαγορευτική Αρχή του Pauli

Α. Κάθε ηλεκτρόνιο έχει διαφορετική τετράδα κβαντικών αριθμών  (n, l, m_l, m_s )(περιγράφεται από την δική του κυματοσυνάρτηση ). ;Έτσι ένα τροχιακό, μπορεί να χωρέσει μέχρι 2 ηλεκτρόνια. 

Έτσι προχωράει η δόμηση με τις εξής τετράδες κβαντικών αριθμών με σειρά n, l, m_l, m_s.

Για το πρώτο ηλεκτρόνιο 1, 0, 0, +1/2

Για το δεύτερο ηλεκτρόνιο 1, 0, 0, +1/2

Για το τρίτο ηλεκτρόνιο 2, 0, 0, +1/2

Για το τέταρτο  ηλεκτρόνιο 2, 0, 0, -1/2

Για το πέμτο  ηλεκτρόνιο 2, 1, -1, +1/2

Για το έκτο ηλεκτρόνιο 2, 1, -1, -1/2

Για το εβδομο ηλεκτρόνιο 2, 1, 0, +1/2

Για το όγδοο ηλεκτρόνιο 2, 1, 0, -1/2

Για το ένατο ηλεκτρόνιο 2, 1, 1, +1/2

Για το δέκατο ηλεκτρόνιο 2, 1, 0, -1/2

κ.ο.κ.

(sel 14) Αρχή της Ελαχίστης Ενέργειας 

Κατά την ηλεκτρονιακή δόμηση, τα ηλεκτρόνια οφείλουν  να καταλαμβάνουν στοιβάδες με την μικρότερη δυνατή ενέργεια. Στην ηλεκτρονιακή δόμηση ενός ατόμου,  τα πρώτα ηλεκτρόνια που τοποθετούνται  στις  μέσα στοιβάδες, κοντά στον πυρήνα, που έχουν μικρότερη ενέργεια και τα επόμενα σε κάθε μια που συναντούν προς τα έξω, ελεύθερη, αρκεί να έχει την μικρότερη δυνατή ενέργεια. Άρα λοιπόν, πρώτα συμπληρώνεται η πρώτη ηλεκτρονιακή στοιβάδα η Κ (n=1 ) μετά η δεύτερη L (n=2 ), μετά η τρίτη M (n=3) μετά η τέταρτη Ν (n=4). Στην αρχή αυτό ισχύει  ακριβώς. Όμως από ένα σημείο και μετά, παρατηρείται ότι ορισμένες υποστοιβάδες αργούν να συμπληρωθούν και συμπληρώνονται προηγουμένως ορισμένες οι υποστοιβάδες των  επόμενων στοιβάδων και μετά αυτές. Ο λόγος είναι ότι κάποιες φορές, οι πιο έξω υποστοιβάδες έχουν χαμηλότερη ενέργεια από αυτές που έμειναν μέσα ασυμπλήρωτες διότι εκτός από την έλξη του πυρήνα δυνάμεις ασκούν και τα ηλεκτρόνια των στοιβάδων που έχουν ήδη συμπληρωθει. 

Έτσι διαφοροποιούνται οι ενεργειακές στάθμες των υποστοιβάδων της ίδιας στοιβάδας. 

Συμπληρώνονται λοιπόν πρώτα και στην συνέχεια κάποιες εσωτερικές. Για να έχουμε εικόνα της στάθμης της ενέργειας κάθε στοιβάδας, χρησιμοποιούμε ένα διάγραμμα. Τα ηλεκτρόνια τοποθετούνται σύμφωνα με τα βελάκια

Σύμφωνα με τα παραπάνω τα ας δούμε πως τοποθετούνται  26 ηλεκτρόνια στο άτομο του σιδήρου, στη θεμελιώδη του κατάσταση. Πρώτα τοποθετούνται δύο ηλεκτρόνια στην υποστιβάδα 1s, και γράφουμε 1s², μετά τοποθετούμε δύο ηλεκτρόνια στην υποστιβάδα 2s (1s² 2s²), ακολουθούν έξι ηλεκτρόνια στην υποστιβάδα 2p (1s² 2s² 2p⁶ ), δύο ηλεκτρόνια στην υποστιβάδα 3s (1s² 2s² 2p⁶ 3s²), έξι στην υποστιβάδα 3p (1s² 2s² 2p⁶ 3s² 3p⁶) και δύο στην 4s (1s² 2s² 2p⁶ 3s² 3p⁶ 4s²). Τα τελευταία έξι ηλεκτρόνια πάνε στην υποστιβάδα 3d, η οποία χωράει συνολικά δέκα ηλεκτρόνια. Έτσι, η ηλεκτρονιακή δομή του σιδήρου είναι: 

 

ΠΗΓΕΣ

Χημεία Γ Λυκείου θετικής κατεύθυνσης 

https://dimitra-spanoy.webnode.gr/news/η-ιστορία-των-φυσικών-επιστημών-μέρος-πέμπτο-η-/

news/η-ιστορία-των-φυσικών-επιστημών-μέρος-έβδομο%3a/

https://el.wikipedia.org/wiki/Κβαντική_μηχανική

ebooks.edu.gr3069 × 2309

atomikatroxiaka.weebly.com664 × 604

slideplayer.gr960 × 720

 

 

 

 

 

 

 

 

 

 

 

εκτος βιβλίου αλλά χρησιμο

Για να καταλάβουμε αν πάρουμε τον πρώτο τύπο της ενέργειας και αντικαταστήσουμε  

 για το απλουστερο άτομο  του υδρογόνου,  οι 4 πρώτες ενεργειακές στάθμες έχουν ενέργεια (αν την μετατρέψουμε σε ev)

 

 

 

ΠΗΓΕΣ

Χημεία Γ Λυκείου θετικής κατεύθυνσης

https://dimitra-spanoy.webnode.gr/news/η-ιστορία-των-φυσικών-επιστημών-μέρος-πέμπτο-η-/

 

 

 

 υπό κατεργασία

Ο

 

 

 

 

Για να διεγερθεί ένα ηλεκτρόνιο και να περάσει από την πρώτη θεμελιώδη και χαμηλώτερης ενέργειας στάθμη με n=1 και ενέργεια -13,6eV στην δεύτερη χρειάζεται ενέργεια ίση με την διαφορά τους δηλαδή 10,2eV  ενώ από την δεύτερη στην τρίτη(2,18.10^-18 joule) ενώ από την δεύτερη στην τρίτη 1,89 eV  σύμφωνα με την διαφορά ενέργειας  μεταξύ των δύο

Δηλαδή για να ξεφύγει από την θεμελιώδη και σαθερή κατάσταση που βρίσκεται συνήθως πρέπει να απορροφήσει το μεγαλύτερο ποσό ενέργειας, πολύ μεγαλύτερο από αυτό που χρειάζεται για να περάσει από την δεύτερη στην τρίτη  κι ακόμα πιο μεγάλο από όσο χρειάζεται για να περάσει από την τρίτη στην τέταρτη στάθμη. Είναι λοιπόν δύσκολο και χρειάζεται την μεγαλύτερη ενέργεια για να ξεφύγουν τα άτομα και κατ επέκταση όλα τα υλικά σώματα από την θεμελιώδη και σταθερή κατάσταση , όπως τα ξέρουμε συνήθως. Η απορροφούμενη ακτινοβολία πρέπει να είναι μιας συγκεκριμένης συχνότητας  σύμφωνα με την θεμελιώδη εξίσωση των κυμάτων E=h.ν

από όπου προκύπτει ότι η συχνότητα του φωτονίου που απορροφάται κάθε φορά για την διέγερση του ηλεκτρονίου ενός ατόμου βρίσκεται κάτω από αυστηρούς περιορισμούς, Εδώ για παράδειγμα να είνα ΔΕ/h ν= 1,54.10¹⁶Hz όπου η ΔΕ είναι Ε₂-Ε₁ θεμελιώδους και πρώτης διεγερμένης

Για την θέση του ηλεκτρονίου:

 Παρατηρούμε πως η στροφορμή του ηλεκτρονίου είναι  μέγεθος  κβαντισμένο και είναι ακέραιο πολλαπλάσιο της ποσότητας  , όπου h είναι η σταθερά του Plank.

    Τ

ο μέτρο της στροφορμής του περιστρεφόμενου ηλεκτρόνιου δίνεται από την σχέση  L=m u r και από εδώ βρίσκουμε επίσης και την ακτίνα της τροχαιάς r=L/mu όταν πάρουμε υπ΄όψη την  κβάντωση  της στροφορμής 

Κβάντωση  παρατηρείται και στην απόσταση από τον πυρήνα (ακτίνα τροχαιάς προς το παρόν ) που μπορεί να κινούνται τα ηλεκτρόνια ενός οποιουδήποτε πια ατόμου. 

(Αργότερα το 1927 καταρρίπτεται η στενή  έννοια της κίνησης των ηλεκτρονίων σε καθορισμένη κυκλική τροχαιά γύρω από τον πυρήνα που αντικαθίσταται από την πυκνότητα πθανότητας ηλεκτρονιακού φορτίου )

τελικά όμως ισχύει πως

Τα άτομα από τα οποία δομείται η ύλη βασίζουν την κατασκευή τους στην κβάντωση της ενέργειας των ηλεκτρονιακών στοιβάδων  και της απόστασης που έχει σε κάθε μια στοιβάδα από τον πυρήνα

• Κβάντωση υπάρχει στην ενέργεια που έχει κάθε μια τροχαιά του ατόμου στην οποία περιστρέφονται τα ηλεκτρόνια c,2..
• Η ποσότητα της ενέργειας που απορροφάται ή εκπέμπεται  κατά την διέγερση ή αποδιέγερση ενός ατόμου είναι επίσης κβαντισμένες 
•  Κβάντωση υπάρχει επίσης και στις αποστάσεις των τροχαιών περιστροφής από τον πυρήνα (προς το παρός το λέμε ακτίνα)
•